Simple Machines Chapter Notes | Technical Science for Grade 10 PDF Download
| Table of contents |

|
| Levers are Simple Machines |

|
| The Law of Moments in Levers |

|
| Mechanical Advantage |

|
| Points to Remember |

|
| Difficult Words |

|
| Summary |

|
Levers are Simple Machines
This section introduces levers as simple machines, their components, types, and how they provide mechanical advantage.
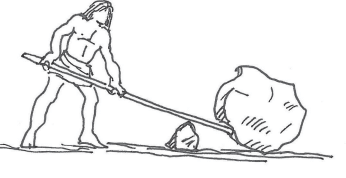 Early man’s stick was a simple machine.
Early man’s stick was a simple machine.
What is a Simple Machine?
- Definition: A simple machine is a device that makes a physical task easier by changing the magnitude of the input force needed to do the work.
- Explanation: Simple machines multiply the effort applied, reducing the force required to perform tasks like lifting or moving objects.
- Example: A stick used by early humans to move a rock was a simple machine, acting as a lever to make the task easier.
Levers as Simple Machines
- Definition: A lever is a simple machine that rotates around a fixed point to move a load with less effort.
- Explanation: Levers provide a mechanical advantage, making tasks like opening a door, stapling paper, or cutting easier.
- Historical Context: Early humans used sticks as levers to dig roots or move rocks, gaining mechanical advantage.
Everyday Examples:
- Turning a door handle.
- Using a stapler.
- Cutting with scissors.
Components of a Lever
- Fulcrum: The point around which the lever rotates, acting as the pivot.
- Effort (Input): The force applied by the user to the lever to perform the task.
- Load (Output): The force or weight the lever is used to overcome or balance.
- Explanation: All levers have these three components, which work together to achieve the desired effect.
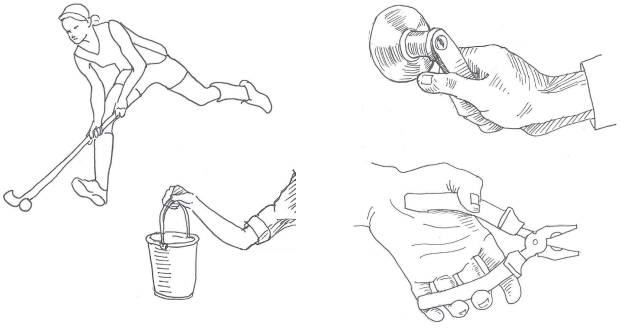 Levers we use every day
Levers we use every day
Types of Levers
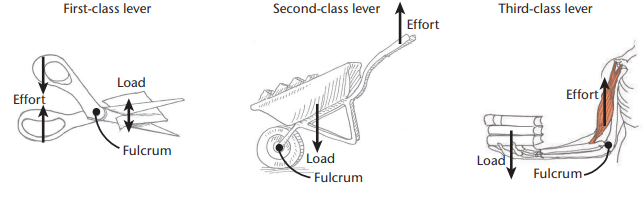
Explanation: Levers are classified into three types based on the relative positions of the fulcrum, load, and effort. Each type has different characteristics and mechanical advantages.
Characteristics of the three types of levers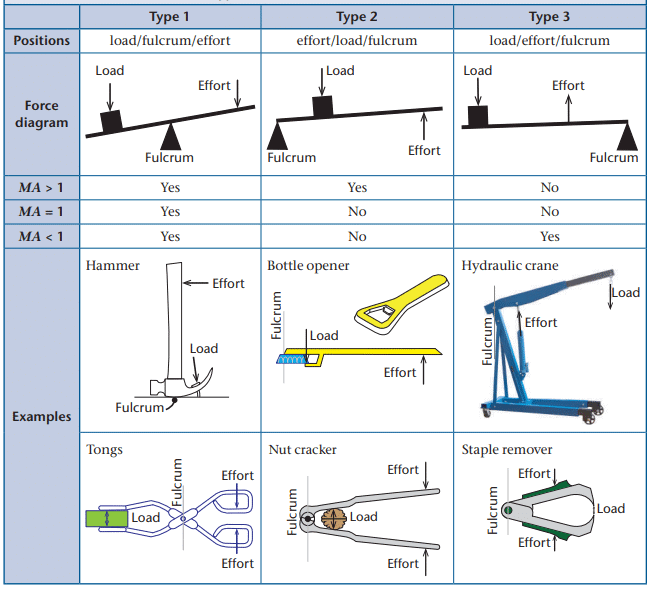
First-Class Lever:
- The fulcrum is between the load and effort.
- MA can be greater than, equal to, or less than 1, depending on the distances from the fulcrum.
- Examples: A crowbar (MA > 1), seesaw (MA = 1), or pliers (MA < 1).
Second-Class Lever:
- The load is between the effort and fulcrum.
- Always provides MA > 1, making it ideal for lifting heavy loads with less effort.
- Examples: A wheelbarrow or bottle opener.
Third-Class Lever:
- The effort is between the load and fulcrum.
- Always provides MA < 1, requiring more effort but useful for precision or speed.
- Examples: Tweezers or a fishing rod.
The Law of Moments in Levers
This section explains how the Law of Moments is used to analyze levers in equilibrium, calculating forces and distances.
Moments in Levers
Definition: A moment is the turning effect produced by a force acting at a distance from the fulcrum.
Formula: Moment = Force × Perpendicular Distance from the fulcrum to the line of the force.
- In symbols: M = F × d
- M: Moment (newton meters, N m)
- F: Force (newtons, N)
- d: Distance (meters, m)
Explanation: The size of the moment depends on the force’s magnitude and the distance from the fulcrum. The direction is either clockwise or anti-clockwise.
Example: In a lever, a force applied farther from the fulcrum creates a larger moment, making it easier to move the load.
Levers in Equilibrium
- Definition: A lever is in equilibrium when it is not rotating, meaning the clockwise and anti-clockwise moments are balanced.
- Explanation: When the effort moment equals the load moment, the lever is stationary, allowing analysis using the Law of Moments.
- Law of Moments: The sum of clockwise moments equals the sum of anti-clockwise moments.
In symbols: MCW = MACW
Example: On a seesaw, if two children balance perfectly, the clockwise moment (one child) equals the anti-clockwise moment (the other child).
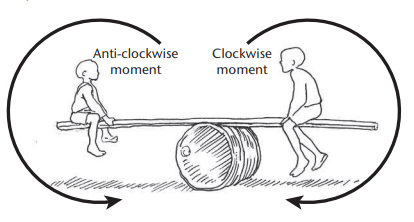
Applying the Law of Moments
Notation:- FL: Load force (newtons, N)
- FE: Effort force (newtons, N)
- dL: Length of the load arm (meters, m)
- dE: Length of the effort arm (meters, m)
Process:
- For a lever in equilibrium, use MCW = MACW.
- Calculate moments: FE × dE = FL × dL.
- Rearrange to find unknown forces or distances.
Examples:
Crowbar (Type 1 Lever): To extract a nail requiring 100 N, with dL = 0.1 m and dE = 0.6 m:
- FE × 0.6 = 100 × 0.1
- FE = (100 × 0.1) / 0.6 = 16.7 N
Bottle Opener (Type 2 Lever): To remove a cap requiring 150 N, with dL = 1.5 cm and dE = 7.5 cm:
- FE × 7.5 = 150 × 1.5
- FE = (150 × 1.5) / 7.5 = 30 N
Tweezers (Type 3 Lever): To avoid breaking a tube with a maximum load of 2 N, with dL = 95 mm and dE = 42 mm:
- FE × 42 = 2 × 95
- FE = (2 × 95) / 42 = 4.5 N
Mechanical Advantage
This section covers mechanical advantage (MA), how to calculate it, and how to use it to find forces or arm lengths in levers.
What is Mechanical Advantage?
Definition: Mechanical advantage (MA) is the factor by which a lever multiplies the input force to overcome a load.Explanation: MA is a unitless number that shows how much easier a task becomes when using a lever. It compares the output force (load) to the input force (effort) or the effort arm to the load arm.
Formulas:
- MA = FL / FE (ratio of load to effort)
- MA = dE / dL (ratio of effort arm to load arm)
Calculating Mechanical Advantage
Using Forces:Example: A lever moves a 700 N load with a 350 N effort.
MA = FL / FE = 700 / 350 = 2
Example: Circlip pliers open a circlip with a 12 N load using a 4 N effort.
MA = 12 / 4 = 3
Using Distances:
Example: A lever has an effort arm of 1.2 m and a load arm of 0.3 m.
MA = dE / dL = 1.2 / 0.3 = 4
Example: Circlip pliers have an effort arm of 7.0 cm and a load arm of 3.5 cm.
MA = 7.0 / 3.5 = 2
Calculating Load or Effort Using MA
Formulas:Load: FL = MA × FE (newtons)
Effort: FE = FL / MA (newtons)
Examples:
- Crowbar: MA = 5, load = 1000 N.
FE = 1000 / 5 = 200 N - Bolt Cutter: MA = 15, load = 3000 N, maximum effort = 300 N.
Possible load: FL = 300 × 15 = 4500 N (can cut the bolt since 4500 N > 3000 N).
Calculating Load Arm or Effort Arm Using MA
Formulas:- Load arm: dL = dE / MA (meters)
- Effort arm: dE = dL × MA (meters)
Examples:
- Lever: MA = 6, load arm = 0.2 m.
dE = 0.2 × 6 = 1.2 m - Fire Tongs: MA = 0.2, effort arm = 0.1 m.
dL = 0.1 / 0.2 = 0.5 m (can reach coals 0.5 m away).
MA and Lever Types
- Type 1 Lever: MA can be > 1, = 1, or < 1, depending on arm lengths.
- Type 2 Lever: Always MA > 1, as the effort arm is longer than the load arm.
- Type 3 Lever: Always MA < 1, as the effort arm is shorter than the load arm.
Cost of Mechanical Advantage
- Explanation: According to the law of conservation of energy, a lever with MA > 1 requires the effort to move a greater distance than the load.
- Example: If MA = 4, and the load moves 10 cm, the effort must move 40 cm.
- Implication: Higher MA reduces the force needed but increases the distance over which the effort is applied.
Points to Remember
- A lever is a simple machine that makes tasks easier by multiplying the input force.
- All levers have a fulcrum (pivot), effort (input force), and load (output force).
- First-class levers have the fulcrum between the load and effort, with MA > 1, = 1, or < 1.
- Second-class levers have the load between the effort and fulcrum, always with MA > 1.
- Third-class levers have the effort between the load and fulcrum, always with MA < 1.
- The Law of Moments states that in equilibrium, clockwise moments equal anti-clockwise moments (MCW = MACW).
- Mechanical advantage (MA) is the ratio of load to effort (FL / FE) or effort arm to load arm (dE / dL).
- MA > 1 means less effort is needed but the effort moves a greater distance.
- Use MA to calculate unknown forces (FL = MA × FE, FE = FL / MA) or arm lengths (dE = dL × MA, dL = dE / MA).
- The conservation of energy means a higher MA requires a longer effort distance.
Difficult Words
- Simple Machine: A device that makes physical tasks easier by changing the input force needed.
- Lever: A simple machine that rotates around a fulcrum to move a load with less effort.
- Fulcrum: The fixed point around which a lever rotates.
- Effort: The force applied to a lever by the user to perform a task.
- Load: The force or weight a lever is used to overcome or balance.
- Mechanical Advantage (MA): The factor by which a lever multiplies the input force, calculated as FL / FE or dE / dL.
- Moment: The turning effect of a force, calculated as force × distance from the fulcrum.
- Equilibrium: The state where a lever is balanced, with clockwise and anti-clockwise moments equal.
- Clockwise: Rotation in the direction of a clock’s hands.
- Anti-Clockwise: Rotation opposite to a clock’s hands.
- Load Arm: The distance from the fulcrum to the point where the load is applied.
- Effort Arm: The distance from the fulcrum to the point where the effort is applied.
Summary
This chapter focuses on levers, simple machines that make physical tasks easier by multiplying the input force through mechanical advantage. Levers consist of a fulcrum (pivot), effort (input force), and load (output force), and are classified into three types: first-class (fulcrum between load and effort, MA > 1, = 1, or < 1), second-class (load between effort and fulcrum, MA > 1), and third-class (effort between load and fulcrum, MA < 1). The Law of Moments, stating that clockwise moments equal anti-clockwise moments in equilibrium, is used to analyze levers and calculate forces or distances. Mechanical advantage (MA) is the ratio of load to effort or effort arm to load arm, allowing calculation of forces (FL = MA × FE, FE = FL / MA) or arm lengths (dE = dL × MA, dL = dE / MA). A higher MA reduces effort but requires the effort to move a greater distance, per the conservation of energy. These principles are essential for understanding how levers function in everyday tools like crowbars, bottle openers, and tweezers.
|
1 videos|77 docs|5 tests
|
FAQs on Simple Machines Chapter Notes - Technical Science for Grade 10
| 1. What are the different types of levers and how do they function? |  |
| 2. How is the mechanical advantage of a lever calculated? |  |
| 3. What is the Law of Moments and how does it apply to levers? |  |
| 4. Can you provide examples of levers in everyday life? |  |
| 5. What are some key points to remember when studying simple machines, particularly levers? |  |














