Simultaneous (Linear) Equations (Including Problems) Chapter Notes | Mathematics Class 9 ICSE PDF Download
Introduction
Imagine you're planning a trip with your friends, and you need to figure out how many train tickets and snacks to buy with a fixed budget. This is where simultaneous linear equations come to the rescue! These equations help solve real-life problems by finding values for multiple variables that satisfy more than one condition at the same time. In this chapter, we dive into the exciting world of solving two linear equations together, using methods like substitution, equating coefficients, and cross-multiplication. We'll also explore how these equations apply to practical scenarios like numbers, fractions, ages, and even train fares. Get ready to unlock the power of algebra to solve puzzles that make math both fun and meaningful!
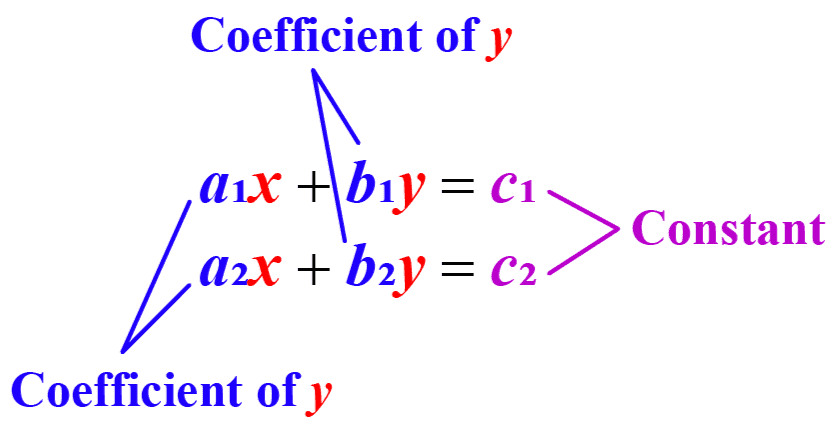
- A linear equation is of the form ax + by + c = 0, where a, b, and c are real numbers, and x and y are variables with a degree of 1.
- Simultaneous linear equations are two or more linear equations with the same variables (e.g., x and y).
- The solution to simultaneous equations is a pair of values for the variables that satisfy all equations in the system.
Example: For equations 2x - y = 1 and 3x + y = 14, substituting x = 3 and y = 5 satisfies both:
- 2x - y = 2 × 3 - 5 = 1 (True)
- 3x + y = 3 × 3 + 5 = 14 (True)
- Hence, x = 3 and y = 5 is the solution.
Methods of Solving Simultaneous Equations
Solving simultaneous equations means finding values of the variables that satisfy both equations.
Three algebraic methods are commonly used to solve them:
- Method of elimination by substitution
- Method of elimination by equating coefficients
- Method of cross-multiplication
Method of Elimination By Substitution
This method involves expressing one variable in terms of the other and substituting it into the second equation.
Steps:
- Step 1: From one equation, express one variable (e.g., y) in terms of the other (e.g., x).
- Step 2: Substitute this expression into the other equation and solve for the remaining variable.
- Step 3: Substitute the value found in Step 2 back into the expression from Step 1 to find the other variable.
Example: Solve x + y = 7 and 3x - 2y = 11
Step 1: From x + y = 7, get y = 7 - x.
Step 2: Substitute y = 7 - x in 3x - 2y = 11:
- 3x - 2(7 - x) = 11
- 3x - 14 + 2x = 11
- 5x = 25, so x = 5
Step 3: Substitute x = 5 in y = 7 - x: y = 7 - 5 = 2.
Solution: x = 5, y = 2.
Alternate Method: Solve the same equations by expressing x in terms of y.
Step 1: From x + y = 7, get x = 7 - y.
Step 2: Substitute x = 7 - y in 3x - 2y = 11:
- 3(7 - y) - 2y = 11
- 21 - 3y - 2y = 11
- -5y = -10, so y = 2
Step 3: Substitute y = 2 in x = 7 - y: x = 7 - 2 = 5.
Solution: x = 5, y = 2.
Method of Elimination By Equating Coefficients
This method makes the coefficients of one variable equal in both equations, then adds or subtracts to eliminate that variable.
Steps:
- Step 1: Multiply one or both equations by numbers to make the coefficients of x or y equal.
- Step 2: Add or subtract the equations to eliminate one variable.
- Step 3: Solve the resulting equation for the remaining variable.
- Step 4: Substitute the value into one of the original equations to find the other variable.
Example: Solve 3x - 4y = 10 and 5x - 3y = 24
- 5 × (3x - 4y = 10) → 15x - 20y = 50
- 3 × (5x - 3y = 24) → 15x - 9y = 72
Step 2: Subtract: (15x - 20y) - (15x - 9y) = 50 - 72 → -11y = -22, so y = 2.
Step 3: Substitute y = 2 in 3x - 4y = 10: 3x - 4 × 2 = 10 → 3x = 18, so x = 6.
Solution: x = 6, y = 2.
Alternate Method for Special Case: Solve 65x - 33y = 97 and 33x - 65y = 1, where coefficients of x and y are swapped.
- Step 1: Add equations: (65x - 33y) + (33x - 65y) = 97 + 1 → 98x - 98y = 98 → x - y = 1.
- Step 2: Subtract equations: (65x - 33y) - (33x - 65y) = 97 - 1 → 32x + 32y = 96 → x + y = 3.
- Step 3: Solve x - y = 1 and x + y = 3: Add → 2x = 4 → x = 2, then x + y = 3 → y = 1.
Solution: x = 2, y = 1.
Method of Cross-Multiplication
This method uses a formula to solve equations of the form
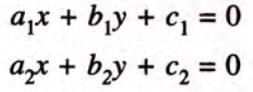
Formula:

Steps:
- Step 1: Rewrite equations in standard form: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
- Step 2: Identify coefficients a1, b1, c1, a2, b2, c2.
- Step 3: Apply the formula to find x and y.
Example: Solve 2x + 3y = 6 and 6x - 5y = 4
Step 1: Rewrite: 2x + 3y - 6 = 0 and 6x - 5y - 4 = 0.
Step 2: Coefficients: a1 = 2, b1 = 3, c1 = -6, a2 = 6, b2 = -5, c2 = -4.
Step 3: Apply formula:
- x = [(3 × -4) - (-5 × -6)] / [(2 × -5) - (6 × 3)] = (-12 - 30) / (-10 - 18) = -42 / -28 = 3/2.
- y = [(-6 × 6) - (-4 × 2)] / [-28] = (-36 + 8) / -28 = -28 / -28 = 1.
Solution: x = 3/2, y = 1.
Equations Reducible to Linear Equations
Some equations have variables in denominators, which can be transformed into linear equations.
Steps:
- Step 1: Substitute variables like 1/x = a or 1/y = b to simplify denominators.
- Step 2: Solve the resulting linear equations using any method (substitution, equating coefficients, or cross-multiplication).
- Step 3: Convert back to original variables by solving for x and y.
Example: Solve 7/x + 8/y = 2 and 2/x + 13/y = 22
Step 1: Let 1/x = a and 1/y = b, so equations become: 7a + 8b = 2 and 2a + 13b = 22.
Step 2: Multiply first by 2 and second by 7:
- 14a + 16b = 4
- 14a + 91b = 154
- Subtract: (91b - 16b) = 154 - 4 → 75b = 150 → b = 2.
Step 3: Substitute b = 2 in 2a + 13b = 22: 2a + 13 × 2 = 22 → 2a = -4 → a = -2.
Step 4: Since a = 1/x = -2 → x = -1/2, and b = 1/y = 2 → y = 1/2.
Solution: x = -1/2, y = 1/2.
Alternate Method 1: Solve 30/(x - y) + 44/(x + y) = 10 and 40/(x - y) + 55/(x + y) = 13 by direct manipulation.
Step 1: Multiply first equation by 4 and second by 3:
- 120/(x - y) + 176/(x + y) = 40
- 120/(x - y) + 165/(x + y) = 39
Step 2: Subtract: [176/(x + y) - 165/(x + y)] = 40 - 39 → 11/(x + y) = 1 → x + y = 11.
Step 3: Substitute x + y = 11 in first equation: 30/(x - y) + 44/11 = 10 → 30/(x - y) = 6 → x - y = 5.
Step 4: Solve x + y = 11 and x - y = 5: x = 8, y = 3.
Solution: x = 8, y = 8.
Alternate Method 2: Use substitutions x - y = a and x + y = b.
Step 1: Let x - y = a and x + y = b, so equations become: 30/a + 44/b = 10 and 40/a + 55/b = 13.
Step 2: Multiply first by 4 and second by 3:
- 120/a + 176/b = 40
- 120/a + 165/b = 39
Step 3: Subtract: 11/b = 1 → b = 11 → x + y = 11.
Step 4: Substitute b = 11 in 30/a + 44/11 = 10 → 30/a = 6 → a = 5 → x - y = 5.
Step 5: Solve x + y = 11 and x - y = 5: x = 8, y = 3.
Solution: x = 8, y = 3.
Alternate Method 3: Use substitutions 1/(x - y) = a and 1/(x + y) = b.
Step 1: Let 1/(x - y) = a and 1/(x + y) = b, so equations become: 30a + 44b = 10 and 40a + 55b = 13.
Step 2: Solve using elimination:
- Multiply first by 4 and second by 3, then subtract to find b = 1/11, so x + y = 11.
- Substitute b = 1/11 in first equation to find a = 1/5, so x - y = 5.
Step 3: Solve x + y = 11 and x - y = 5: x = 8, y = 3.
Solution: x = 8, y = 3.
Problems Based on Simultaneous Equations
Simultaneous equations can solve real-world problems by setting up equations based on given conditions.
General Steps:
- Step 1: Define two variables (e.g., x and y) for the unknowns.
- Step 2: Form two equations based on the problem's conditions.
- Step 3: Solve the equations using any method.
A. Based on Numbers
Problems involve finding two numbers based on their sum, difference, or other relationships.
Example: The sum of two numbers is 12, and their difference is 2. Find the numbers.
- Step 1: Let the numbers be x and y.
- Step 2: Equations: x + y = 12 and x - y = 2.
- Step 3: Solve: Add equations → 2x = 14 → x = 7. Substitute x = 7 in x + y = 12 → y = 5.
Solution: Numbers are 7 and 5.
B. Based on Fractions
Problems involve finding a fraction where numerator and denominator satisfy certain conditions.
Example: The numerator of a fraction is decreased by 1, it becomes 2/3; if the denominator is increased by 5, it becomes 1/2. Find the fraction.
- Step 1: Let the fraction be x/y.
- Step 2: Equations: (x - 1)/y = 2/3 → 3x - 2y = 3, and x/(y + 5) = 1/2 → 2x = y + 5.
- Step 3: Solve: From 2x = y + 5, get y = 2x - 5. Substitute in 3x - 2y = 3 → 3x - 2(2x - 5) = 3 → x = 7, y = 9.
Solution: Fraction is 7/9.
C. Based on Two-Digit Numbers
Problems involve two-digit numbers where digits satisfy conditions like sum, difference, or reversal.
Example: The sum of digits of a two-digit number is 7. If digits are reversed, the new number increased by 3 equals 4 times the original number. Find the number.
- Step 1: Let tens digit be x, units digit be y. Number = 10x + y.
- Step 2: Equations: x + y = 7 and 10y + x + 3 = 4(10x + y).
- Step 3: Simplify second equation: 10y + x + 3 = 40x + 4y → 39x - 6y = 3. Solve with x + y = 7 → x = 1, y = 6.
Solution: Number = 10 × 1 + 6 = 16.
D. Based on Ages
Problems involve finding present or past ages based on ratios or differences over time.
Example: Present ages of A and B are in ratio 9:4. Seven years hence, the ratio will be 5:3. Find their present ages.
- Step 1: Let A's age = x years, B's age = y years.
- Step 2: Equations: x/y = 9/4 → 4x - 9y = 0, and (x + 7)/(y + 7) = 5/3 → 3x - 5y = 14.
- Step 3: Solve: x = 18, y = 8.
Solution: A's age = 18 years, B's age = 8 years.
E. Based on C.P. and S.P.
Problems involve finding cost price (C.P.) or selling price (S.P.) based on profit percentages.
Example: A farmer sold a calf and cow for ₹7600, making 25% profit on calf and 10% on cow. For ₹7675, he makes 10% on calf and 25% on cow. Find C.P. of each.
- Step 1: Let C.P. of calf = ₹x, cow = ₹y.
- Step 2: Equations: (5x/4) + (11y/10) = 7600 → 25x + 22y = 152000, and (11x/10) + (5y/4) = 7675 → 22x + 25y = 153500.
- Step 3: Solve: x = 3000, y = 3500.
Solution: C.P. of calf = ₹3000, cow = ₹3500.
F. Based on Time and Work
Problems involve finding time taken by individuals to complete work based on their combined work rates.
Example: A and B together do a work in 15 days. A's one day's work is 1.5 times B's. Find time each takes alone.
- Step 1: Let A take x days, B take y days.
- Step 2: Equations: 1/x + 1/y = 1/15, and (1/x) = 1.5 × (1/y) → y = 1.5x.
- Step 3: Solve: Substitute y = 1.5x in 1/x + 1/(1.5x) = 1/15 → x = 25, y = 37.5.
Solution: A takes 25 days, B takes 37.5 days.
G. Miscellaneous Problems
Problems cover various scenarios like quantities, fares, or mixtures solvable by simultaneous equations.
Example: A and B have oranges. If B gives 10 to A, A has twice B's remaining. If A gives 10 to B, they have equal oranges. Find their oranges.
- Step 1: Let A have x oranges, B have y oranges.
- Step 2: Equations: x + 10 = 2(y - 10) → x - 2y = -30, and y + 10 = x - 10 → x - y = 20.
- Step 3: Solve: x = 70, y = 50.
Solution: A has 70 oranges, B has 50 oranges.
|
64 videos|165 docs|28 tests
|
FAQs on Simultaneous (Linear) Equations (Including Problems) Chapter Notes - Mathematics Class 9 ICSE
| 1. What are the different methods for solving simultaneous equations? |  |
| 2. How does the method of elimination by substitution work? |  |
| 3. Can you explain the method of elimination by equating coefficients? |  |
| 4. What is the method of cross-multiplication and when is it used? |  |
| 5. What types of problems can be solved using simultaneous equations? |  |
















