Solving Related Rates Problems Chapter Notes | Calculus AB - Grade 9 PDF Download
Related rates problems in calculus focus on determining how quickly one variable changes in relation to the rate of change of another connected variable. These problems often involve geometric shapes or real-world scenarios where multiple quantities are linked through equations, typically with respect to time. To dive deeper into the fundamentals, refer to the Introduction to Related Rates guide.
Steps to Tackle Related Rates Problems
Facing a related rates problem can feel daunting due to the wealth of information provided. However, organizing your approach can make the process manageable. Follow these steps to solve related rates problems effectively:
- Read Thoroughly: Carefully analyze the problem to pinpoint key values, such as known quantities and their rates of change. Highlight or jot down these values for clarity.
- Sketch a Diagram: Draw a visual representation of the scenario, labeling variables and their rates of change to understand their relationships.
- Establish an Equation: Formulate an equation that connects the variables, often based on geometric formulas or given relationships.
- Apply Implicit Differentiation: Differentiate the equation with respect to time (t), using the chain rule for terms involving variables.
- Plug in Known Values: Substitute known quantities and rates into the differentiated equation.
- Solve for the Target Rate: Isolate and solve for the desired rate of change, ensuring units align with the problem’s requirements.
Practice Problems
Let’s apply these steps to two classic related rates problems to solidify your understanding.
Example 1: Expanding Rectangle
A rectangle has a length of 8 feet and a width of 6 feet. The width is increasing at a rate of 2 feet per minute. How fast is the rectangle’s area increasing?
Step 1: Identify Key Information
- Length (l) = 8 ft
- Width (w) = 6 ft
- Rate of change of width (dw/dt) = +2 ft/min
- Rate of change of area (dA/dt) = ?
Step 2: Draw a Diagram
Visualize a rectangle with a fixed length of 8 ft and a width that changes over time. (Refer to a diagram of a rectangle for clarity.)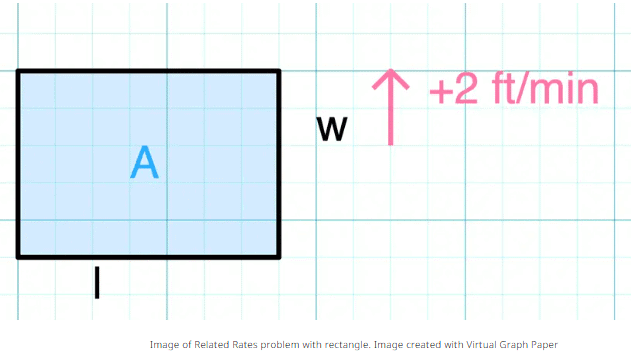 Step 3: Set Up the Equation
Step 3: Set Up the Equation
The area of a rectangle is given by:
A = l × w
Since the length is constant (l = 8), the equation simplifies to:
A = 8w
Step 4: Differentiate
Differentiate with respect to time using the chain rule:
dA/dt = 8 × dw/dt
Step 5: Substitute Known Values
Plug in dw/dt = 2:
dA/dt = 8 × 2 = 16 ft/min
Step 6: Conclusion
The area of the rectangle is increasing at a rate of 16 feet per minute.
Example 2: Sliding Ladder
Consider a 13 meter long ladder leaning against the wall. If the distance between the wall and the bottom of the ladder is increasing at 3 m/s, how fast is the distance between the ground and the top of the ladder changing when the bottom of the ladder is 5 feet away from the wall when it begins sliding?
This question unloaded a lot of information all at once, so take a second to reread the scenario before we get to work. You can do it!
Let’s begin by identifying some key facts and drawing a picture of the scenario.
Known Information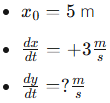
Important Equations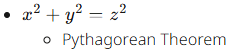
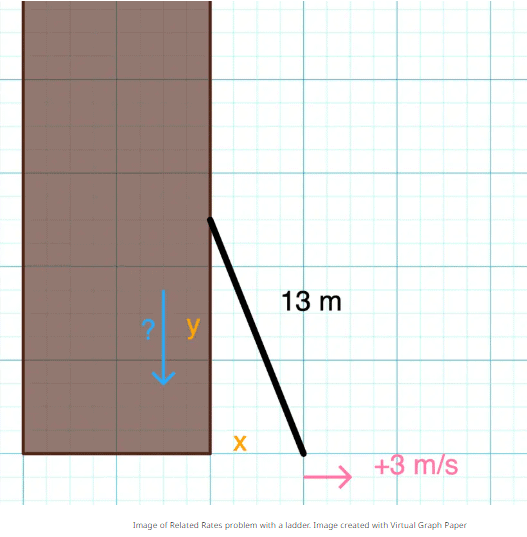 Now we can use the equation relating the side lengths of the triangle made with the ladder, wall, and ground. When looking at the image, we notice that the hypotenuse of the triangle is not changing and we conclude that dz/dt = 0.
Now we can use the equation relating the side lengths of the triangle made with the ladder, wall, and ground. When looking at the image, we notice that the hypotenuse of the triangle is not changing and we conclude that dz/dt = 0.
After directly plugging in any constants into the equation, we can relate the sides with the following equation: x2+y2=132. And now we can finally take the derivative! Don’t forget to use the chain rule since we are taking the derivative with respect to time. Taking the derivative of the main equation gives us: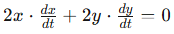
Now let’s plug in all known variables and see what we have to solve for.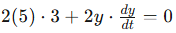
You may have noticed that we have two missing pieces of information: the value of y when x=5 and dy/dt which is our ultimate solution.
We can solve for the value of y by using the Pythagorean Theorem! A triangle will a side length of 5 and a hypotenuse of 13 is actually part of three Pythagorean Triple (5,12,13). But if you didn’t pick that up, we can quickly solve for the missing value of y by just plugging into the equation.
We can then isolate $y$ to get…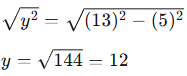
We're almost there!
The final step is to solve for dy/dt. Using algebra, we can isolate dy/dt and get 2(5)⋅3+2(12)⋅ dy/dt = 0 and 15 = -12 dy/dt.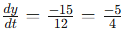
Therefore, we find that the distance between the top of the ladder and the ground is decreasing at a rate of (-5/4) meters per second when the bottom of the ladder is five feet away from the wall.
Wrapping Up
With these steps and examples, you’re equipped to handle related rates problems confidently. These questions are common in AP Calculus exams, appearing in both multiple-choice and free-response sections, testing your ability to apply calculus to dynamic real-world scenarios. Keep practicing, and you’ll master related rates in no time!
Key Terms to Know
- Conical Water Tank: A cone-shaped container, wide at the base and narrowing toward the top, used for holding liquids.
- Depth: The vertical distance from the highest to the lowest point of an object or shape.
- Height: The vertical measurement from the base to the top of an object or shape.
- Proportion: A relationship where two quantities maintain a constant ratio or equality.
- Radius: The distance from the center of a circle to any point on its edge.
- Rate of Change: The speed at which one quantity changes relative to another, often expressed as a ratio.
- Related Rates: A calculus concept for finding how one quantity’s rate of change relates to another’s, using derivatives.
- Volume of a Cone: The space inside a cone, calculated as V = (1/3)πr²h, where r is the base radius and h is the height.
- Volume Formula: An equation to compute the space occupied by a 3D object.
|
26 videos|75 docs|38 tests
|
FAQs on Solving Related Rates Problems Chapter Notes - Calculus AB - Grade 9
| 1. What are related rates problems in calculus? |  |
| 2. How do you identify the variables in a related rates problem? |  |
| 3. What is the first step in solving a related rates problem? |  |
| 4. Why is it important to draw a diagram for related rates problems? |  |
| 5. What common mistakes should be avoided when solving related rates problems? |  |




















