Straight-Line Motion: Connecting Position, Velocity, and Acceleration Chapter Notes | Calculus AB - Grade 9 PDF Download
If you've mastered calculating derivatives, you might be curious about their real-world applications. One fascinating use of derivatives is in analyzing rectilinear motion, which involves studying an object's position, velocity, speed, and acceleration as it moves along a straight line.
Derivatives in Motion Analysis
Derivatives allow us to measure the instantaneous rate of change of a function at a specific point. In the context of motion, this helps us understand how an object's position, velocity, and acceleration change over time.
Position and Velocity
Consider a function x(t) that describes an object's position as a function of time. The first derivative of this function, x'(t) or v(t), represents the velocity—the rate at which the position changes over time. Velocity is a signed quantity, indicating both speed and direction:
- Positive velocity (v(t) > 0): The object moves to the right or in the positive direction.
- Negative velocity (v(t) < 0): The object moves to the left or in the negative direction.
- Speed: The magnitude of velocity, calculated as |v(t)|, representing how fast the object moves regardless of direction.
Acceleration
The derivative of the velocity function, v'(t), or the second derivative of the position function, x''(t), represents acceleration—the rate at which velocity changes. Acceleration provides insight into whether an object is speeding up or slowing down:
- Positive acceleration: Velocity increases in the direction of motion.
- Negative acceleration: Velocity decreases in the direction of motion.
- Zero acceleration (a(t) = 0): The object moves at a constant velocity, with no change in speed or direction.
The relationship between velocity and acceleration determines whether an object is speeding up or slowing down:
- When v(t) and a(t) have the same sign, the object is speeding up.
- When v(t) and a(t) have different signs, the object is slowing down.
In mathematical terms:
- v(t) = x'(t) (velocity is the first derivative of position).
- a(t) = v'(t) = x''(t) (acceleration is the first derivative of velocity or the second derivative of position).
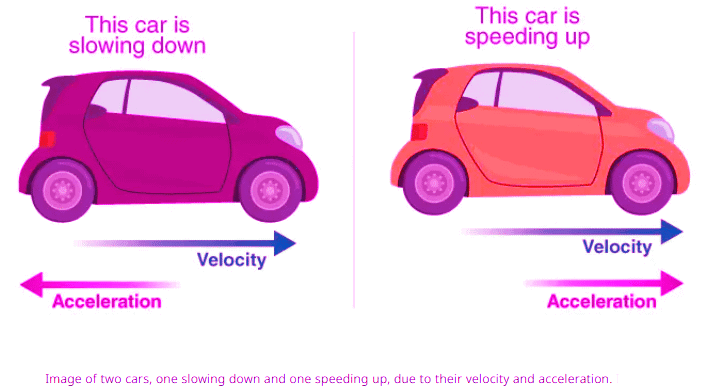
For example, imagine two cars: one accelerating (speeding up) and another decelerating (slowing down). Their behavior depends on the interplay of velocity and acceleration.
Practice Problems in Rectilinear Motion
Let’s apply these concepts with some practice problems to calculate velocity and acceleration.
Problem 1: Finding Acceleration
A particle moves along the x-axis. The function x(t)x(t) gives the particle’s position at any time t>=0.
x(t)=13t−9
What is the particle’s acceleration a(t)a(t) at t=3?
Solution:
Acceleration is the second derivative of the position function. Start with x(t) = 13t - 9:
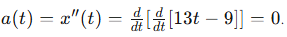
Since a(t) = 0 for all t ≥ 0, the acceleration at t = 3 is 0.
Problem 2: Finding Velocity
A particle moves along the x-axis with the position function x(t) = 4t² - 3t + 16 for t ≥ 0. What is the particle’s velocity v(t) at t = 4?
Solution:
Velocity is the first derivative of the position function. Start with x(t) = 4t² - 3t + 16:
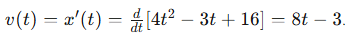
The particle's velocity is v(t) = 8t−3 for all t> = 0, so its velocity at t = 4 is 2929.
Key Terms to Understand
- Absolute Value: The non-negative distance of a number from zero on a number line.
- Acceleration: The rate at which an object’s velocity changes, indicating speeding up, slowing down, or direction change.
- a(t): The acceleration function, showing how velocity changes at a specific time.
- a(t) = 0: Indicates no change in velocity; the object moves at a constant speed or is at rest.
- Derivatives: Mathematical tools to measure the rate of change of a function as its input varies.
- Negative Velocity: Motion in the opposite direction of a chosen positive reference, indicating backward movement.
- Position, Velocity, Acceleration Analysis: A technique to study motion by analyzing position, velocity, and acceleration functions over time.
- Position Function: A function describing an object’s location relative to a reference point, changing with time.
- Positive Velocity: Motion in the direction defined as positive, indicating forward movement.
- Rates of Change: How a quantity changes with respect to another variable, often time.
- Rectilinear Motion: Motion along a straight line, characterized by changes in position, velocity, and acceleration.
- Second Derivative of Position: Represents acceleration, showing how velocity changes over time.
- Speed: The magnitude of velocity, indicating how fast an object moves without regard to direction.
- v'(t): The derivative of velocity, representing the rate of change of speed at a given time.
- v(t) = 0: Indicates the object is momentarily at rest at a specific time.
- x''(t): The second derivative of the position function, representing acceleration.
- x'(t): The first derivative of the position function, representing velocity.
|
26 videos|75 docs|38 tests
|
FAQs on Straight-Line Motion: Connecting Position, Velocity, and Acceleration Chapter Notes - Calculus AB - Grade 9
| 1. What is the difference between position, velocity, and acceleration in rectilinear motion? |  |
| 2. How can I calculate the velocity of an object if I know its position function? |  |
| 3. What does it mean if an object has a negative acceleration? |  |
| 4. How do I determine if an object is at rest using position, velocity, and acceleration? |  |
| 5. Can you explain how to graph position, velocity, and acceleration functions? |  |















