Study Of Gas Laws Chapter Notes | Chemistry Class 9 ICSE PDF Download

Introduction

Behaviour and Characteristic Properties of Gases

• Gases consist of molecules in constant random motion, explained by the kinetic molecular theory.
• Composition: Gases are made of tiny molecules moving in all directions at varying speeds, with negligible size compared to the gas's volume.
• No fixed shape or volume: Weak intermolecular forces allow gas molecules to move freely, adopting the container’s shape.
• Exert pressure: Gas molecules collide with each other and container walls, exerting equal pressure in all directions.
• Highly compressible: Large intermolecular spaces allow gases to compress when pressure is applied, reducing volume.
• Highly expansible: Gases expand when pressure decreases or temperature increases, as molecules move farther apart.
• Low density: Fewer molecules per unit volume result in lower density compared to solids and liquids.
• Diffusion: Gases mix spontaneously due to large intermolecular spaces, forming homogeneous mixtures through molecular motion.
• Liquefaction: Cooling reduces molecular energy, and pressure brings molecules closer, allowing gases to liquefy.

Molecular Motion: Relationship of Temperature, Pressure, and Volume

• Gas molecules are in constant random motion, possessing kinetic energy proportional to absolute temperature (Kelvin).
• Higher temperatures increase molecular motion; lower temperatures decrease it.
• At absolute zero (0 K or -273°C), molecular motion theoretically stops.
• Pressure results from molecular collisions with container walls; increased temperature raises collision frequency and force, increasing pressure.
• If volume is constant, higher temperature increases pressure; if pressure is constant, volume increases with temperature.

The Gas Laws

• Gas laws describe how gases behave under specific conditions of pressure, volume, and temperature.
• Standard variables: Volume (V), Pressure (P), Temperature (T).
• All gases show similar physical behavior, expanding or contracting uniformly under identical conditions.
• Changes in one variable (e.g., pressure) affect the others for a fixed gas mass.

Pressure and Volume Relationship in Gases

• Experiment: Using a syringe with a sealed nozzle, applying weight (pressure) reduces air volume; removing weight increases it.
• Observation: Increased pressure at constant temperature decreases volume; decreased pressure increases volume.

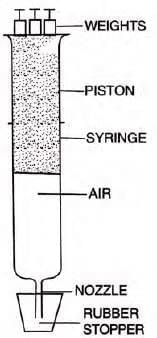
• Conclusion: At constant temperature, gas volume decreases with increased pressure and vice versa.

Boyle’s Law

• At constant temperature, the volume of a fixed mass of dry gas is inversely proportional to its pressure.
• Mathematical expression:
  • Suppose a gas occupies volume V, when its pressure is P₁; then

    

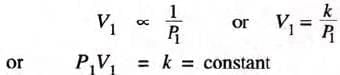
  • If V₂ is the volume occupied when the pressure is P₂ at the same temperature, then

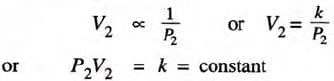
• Alternatively, the product of pressure and volume for a given gas mass at constant temperature is constant.

Graphical Verification of Boyle’s Law

• V vs 1/P: A straight line through the origin confirms inverse proportionality.

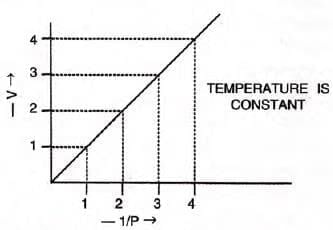
• V vs P: A hyperbolic curve (isotherm) in the first quadrant.

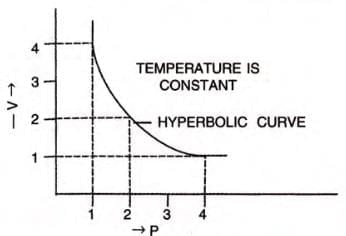
• PV vs P: A straight line parallel to the pressure axis, showing constant PV product.

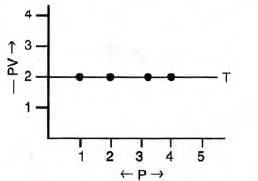
Explanation of Boyle’s Law in Terms of Molecular Motion

•  According to the kinetic theory of gases, number of particles (molecules) present in a given mass and the average kinetic energy possessed by the particles is constant. 
•  If the volume of a given mass of a dry gas is reduced to half its original volume, the same number of particles (molecules) will have half the space to move. As a result, the number of molecules striking at unit area of the walls of the container at a given time will get doubled and so the pressure also gets doubled. 
•  Conversely, if the volume of a given mass of a gas is doubled at constant temperature, the same number of molecules will have double the space to move about. Consequently, the number of molecules striking at unit area of the walls of the container at a given time will become one half of the original value. 
•  Thus, pressure of the gas will be reduced to half of its original pressure. Hence it is seen that if pressure increases, the volume of a given mass of gas decreases at constant temperature (BOYLE’S LAW). 

Significance of Boyle’s Law

•  On increasing pressure, volume decreases. The gas becomes denser. Thus at constant temperature, the d e n s ity of a gas is directly proportional to its pressure. 
•  Atmospheric pressure is low at high altitudes, so air is less dense. Hence, a lesser quantity of oxygen is available for breathing. This is the reason why mountaineers have to carry oxygen cylinders with them. 
•  Note: When air is blown into a balloon, volume and pressure inside the balloon increase. Here, Boyle’s law is not violated as the law is valid for a definite mass, whereas mass increases when more air is blown into the balloon. 

Solved examples 

Example 1: A gas occupies 800 cm³ under 760 nun Hg pressure. Find under what pressure the gas will occupy 380 cm³, the temperature remaining constant.

Solution:

P, = 7 6 0 mm H g; V₁ = 800 cm³

P2 — ? mm H g; V₂ = 380 cm³

By Boyle’s law, P₁V₁ = P₂V₂

Substituting the values,

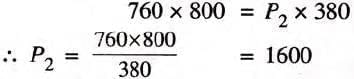
= 1600 mm Hg = 160 cm Hg 

Ans: The required pressure is 160 cm Hg.

Example 2: A gas occupies 600 cm3 under a pressure of 700 nun Hg. Find under what pressure the volume of the gas will be reduced by 20 per cent of its original volume, the temperature remaining constant throughout?

Solution:

By Boyle’s law, P₁V₁ = P₂V₂

Substituting the values, 

700 x 600 = P₂ x 480

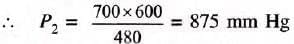
Ans: The required pressure is 875 mm Hg.

Temperature-Volume Relationship in Gases

• Increasing temperature at constant pressure increases gas volume; decreasing temperature reduces it.
• A gas expands or contracts by 1/273 of its volume at 0°C for each 1°C rise or fall in temperature, at constant pressure.

Charles’s Law

• At constant pressure, the volume of a fixed mass of dry gas increases or decreases by 1/273 of its volume at 0°C per 1°C change in temperature.
• Alternatively, volume is directly proportional to absolute (Kelvin) temperature at constant pressure.
• Mathematical expression: V₁/T₁ = V₂/T₂ (constant pressure).

Charles’s law may be restated as: Volume of a given mass of a dry gas is directly proportional to its absolute (Kelvin) temperature, if the pressure remains constant.

Graphical Representation of Charles’s Law

Plotting volume vs. temperature (Kelvin) gives a straight line (isobar), indicating direct proportionality.

Explanation of Charles’s Law in Terms of Molecular Motion

• Kinetic energy of gas molecules is proportional to absolute temperature.
• Higher temperatures increase molecular speed, causing more frequent and forceful collisions.
• At constant pressure, volume increases to accommodate increased molecular motion.

Significance of Charles’s Law

• Volume is proportional to temperature, so density decreases as temperature rises.
• Hot air balloons use heated air, which is less dense, to rise.

Absolute Zero

• At -273°C (0 K), a gas’s volume theoretically becomes zero, as molecular motion ceases.
• Practically, gases liquefy or solidify before reaching this temperature.
• Absolute zero is the lowest theoretical temperature, unattainable in practice.

Absolute or Kelvin Scale of Temperature

• The Kelvin scale starts at -273°C (0 K), with each degree equal to one Celsius degree.
• No degree sign is used for Kelvin values.
• Kelvin simplifies gas law calculations, and all values are positive.

Conversion of Temperature from Celsius Scale to Kelvin Scale and Vice-Versa

• The value on the Celsius scale can be converted to Kelvin scale by adding 273 to it. 

  0°C = 0 + 273 = 273 K

  20°C = 20 + 273 = 293 K 

  27°C = 27 + 273 = 300 K 

  - 273°C = - 273 + 273 = 0 K

• Kelvin scale values can be converted to degree Celsius values by subtracting 273 from it. 

  0 K = 0 - 273 = -273°C

  273 K = 273 - 273 = 0°C (freezing point of water or ice point) 

  13 K = 13 - 273 = -260°C

  373 K = 373 - 273 = 100°C (boiling point of water)

Note: 

• No degree sign is written for absolute temperature values. 
• The size of 1 degree on the Kelvin scale is the same as the size of 1 degree on the Celsius scale i.e. unit size on Kelvin scale is equal to the unit size on Celsius scale. 
• The real advantage of Kelvin scale is that it makes application and use of gas laws simple.
• Even more significantly, all values on Kelvin scale are positive.

Example: 120 cm³ of a gas is taken at 27.3 K. The temperature is then raised to 0 °C. What is the new volume of the gas? The pressure is kept constant. 

Solution:

V₁ = 120 cm³; T, =27.3 K; V₂ = ? cm³

T₂ = 273 K, since 0 °C = 273 K

By Charles’s law,

V₁/T₁ = V₂/T₂

Substituting the values,

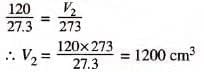
Ans: The gas at 0°C would occupy a volume of 1200 cm³. 

The Gas Equation (Pressure, Volume, and Temperature Relationship)

• Combines Boyle’s and Charles’s laws for a fixed gas mass when both pressure and temperature change.
• Volume is inversely proportional to pressure and directly proportional to absolute temperature.
• Gas equation: P₁V₁/T₁ = P₂V₂/T₂

Example: A gas occupies 572 cm³at 13°C and 725 mm Hg. Find its volume at 24°C and 792 mm Hg.

Solution: Using the gas equation, P₁V₁/T₁ = P₂V₂/T₂

Given: P₁ = 725 mm Hg, V₁ = 572 cm³, T₁ = 13 + 273 = 286 K, P₂ = 792 mm Hg, T₂ = 24 + 273 = 297 K

(725 × 572) / 286 = (792 × V₂) / 297

V₂ = (725 × 572 × 297) / (286 × 792) = 543.75 cm³

Ans: The new volume is 543.75 cm³.

Standard Temperature and Pressure (S.T.P.)

• Standard temperature: 0°C = 273 K
• Standard pressure: 760 mm Hg = 76 cm Hg = 1 atm
• S.T.P. provides a reference for comparing gas volumes, as volume varies with temperature and pressure.
• Balancing pressure and temperature changes can keep gas volume constant.

The Effect of Moisture on Pressure

• Gases collected over water are moist, containing water vapor.
• Total pressure = Pressure of dry gas + Pressure of water vapor (aqueous tension).

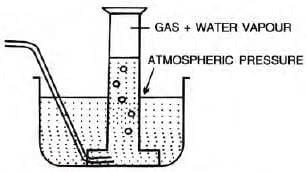
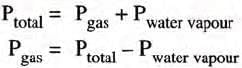
Actual Pressure of gas = Total pressure - Aqueous tension 

Example: 87 cm³of moist nitrogen is at 9°C and 659 mm Hg. Find the volume of dry nitrogen at S.T.P. (Vapor pressure at 9°C = 9 mm Hg).

Solution: Dry nitrogen pressure = 659 - 9 = 650 mm Hg

Using the gas equation: P₁V₁/T₁ = P₂V₂/T₂

Substituting the values,

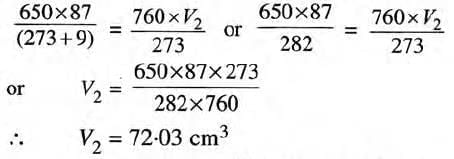
Ans: The volume of dry nitrogen at S.T.P. is 72.03 cm³.

Points to Remember

• Gases lack definite shape and volume, with widely spaced, fast-moving particles.
• Gas behavior is defined by volume (V), pressure (P), and temperature (T).
• Boyle’s Law: P₁V₁ = P₂V₂ (volume inversely proportional to pressure at constant temperature).
• Charles’s Law: V₁/T₁ = V₂/T₂ (volume proportional to Kelvin temperature at constant pressure).
• Absolute zero is -273°C, where molecular motion theoretically stops.
• Temperature conversion: K = °C + 273, °C = K - 273.
• S.T.P.: 0°C (273 K), 760 mm Hg (1 atm).
• Gas equation: P₁V₁/T₁ = P₂V₂/T₂.