Bank Exams Exam > Bank Exams Notes > Quantitative Aptitude for Competitive Examinations > Chapter Notes: The Chain Rule
The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams PDF Download
Welcome to Unit 3’s core concept: the Chain Rule! This essential technique helps us find derivatives of composite functions—functions nested within other functions. If you need a refresher on basic differentiation, revisit Unit 2 before diving in!
Understanding Composite Functions
Composite functions involve one function being applied to the result of another. Suppose we have two functions, f(x) and g(x). Their composite function, denoted (f ∘ g)(x), is defined as:
(f ∘ g)(x) = f(g(x))
Here, g(x) is the inner function, and f(x) is the outer function. This nesting is the key to applying the Chain Rule correctly.
Example of a Composite Function
Let’s look at an example with the functions:
- f(x) = x2
- g(x) = 3x + 1
For the composite function f(g(x)):
- The inner function g(x) = 3x + 1 takes an input x, multiplies it by 3, and adds 1.
- The outer function f(x) = x2 squares the result of g(x).
Thus, the composite function is:
f(g(x)) = (3x + 1)2
Grasping composite functions is crucial for mastering the Chain Rule. Let’s explore the rule itself!
What is the Chain Rule?
The Chain Rule is a differentiation technique for composite functions, similar to the Power Rule, Product Rule, or Quotient Rule from Unit 2. It allows us to differentiate functions where one function is embedded within another. The Chain Rule has two common notations:
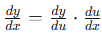
Breaking this down:
- dy/dx is the derivative of the entire function with respect to x.
- u is the inner function.
- dy/du is the derivative of the outer function with respect to the inner function u.
- du/dx is the derivative of the inner function with respect to x.
Alternatively, in function notation:
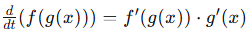
This shows that we differentiate the outer function first (keeping the inner function intact), then multiply by the derivative of the inner function. If there are more nested functions, the process repeats.
Steps to Apply the Chain Rule
To differentiate using the Chain Rule, follow these steps:
- Identify the inner and outer functions.
- Differentiate the outer function with respect to the inner function.
- Differentiate the inner function with respect to x.
- Multiply the two derivatives to obtain the final result.
For a visual summary, check out this helpful diagram from Geeks for Geeks (image not included here; search online for Chain Rule visuals).
Question for Chapter Notes: The Chain RuleTry yourself: What does the Chain Rule help us find?View Solution
Practice Problems with the Chain Rule
Example 1:
Find the derivative of the following function with respect to x.
y = (x2+3x−1)2
- Define your inner and outer functions.
The inner function is u = x2 + 3x − 1. The outer function is y = u2. - Take the derivative of the outer function only!
dy/du = 2u = 2(x2+3x−1)
As you can see, we have not taken the derivative of the inner function u yet. - Take the derivative of the inner function with respect to x.
du/dx = 2x + 3 - Now multiply the two derivatives to get your final answer!
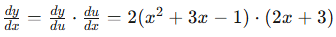
Example 2
Let f(x) = ex and g(x) = ln(x). Find the derivative of y = f(g(x)) with respect to x.
- Define your inner and outer functions.
In this problem, they are more explicit! f(x) is the outer function and g(x) is the inner function. - Take the derivative of the outer function.
f′(g(x)) = eg(x) = eln(x)
The derivative of e^x$ is just $e^x! - Take the derivative of the inner function with respect to x.
g′(x) = 1/x - Then multiply the two derivatives to get your final answer!
f′(g(x)⋅g′(x) = eln(x)⋅ 1/x
Example 3
Find the derivative of the following function; this one may be a bit tougher!
y = 4(5x3 + 2x2 + 6)2.
- Define your inner and outer functions.
The inner function is u = 5x3 + 2x2 + 6 and the outer function is y = 4u2. - Take the derivative of the outer function.
dy/du = 8u = 8(5x3 + 2x2 + 6) - Take the derivative of the inner function with respect to x.
du/dx = 15x2 + 4x - Now multiply the two derivatives to get your final answer!
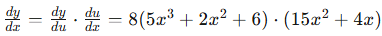
Example 4
How about a function with a square root?
y = √(7x2).
- Define your inner and outer functions.
The inner function is u = 7x2 and the outer function is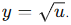
- Take the derivative of the outer function.
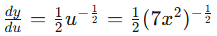
- Take the derivative of the inner function with respect to x.
/fracdudx = 14x - Now multiply the two derivatives to get your final answer!
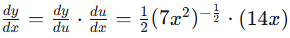
Example 5:
Try taking the derivative of the following function yourself!
f(x) = cos2(3x).
To help you out a little, the inner function is u = cos3x and the outer function is f(x) = u2.
Here’s the answer:
f′(x) = 2(cos3x)⋅ − 3sin(3x)
Question for Chapter Notes: The Chain RuleTry yourself: What is the inner function in the example y = (x² + 3x - 1)²?View Solution
The document The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams is a part of the Bank Exams Course Quantitative Aptitude for Competitive Examinations.
All you need of Bank Exams at this link: Bank Exams
|
166 videos|141 docs|171 tests
|
About this Document
4.89/5
Rating
Oct 04, 2025
Last updated
Related Exams
Document Description: Chapter Notes: The Chain Rule for Bank Exams 2025 is part of Quantitative Aptitude for Competitive Examinations preparation.
The notes and questions for Chapter Notes: The Chain Rule have been prepared according to the Bank Exams exam syllabus. Information about Chapter Notes: The Chain Rule covers topics
like Understanding Composite Functions, What is the Chain Rule?, Practice Problems with the Chain Rule and Chapter Notes: The Chain Rule Example, for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: The Chain Rule.
Introduction of Chapter Notes: The Chain Rule in English is available as part of our Quantitative Aptitude for Competitive Examinations
for Bank Exams & Chapter Notes: The Chain Rule in Hindi for Quantitative Aptitude for Competitive Examinations course.
Download more important topics related with notes, lectures and mock test series for Bank Exams
Exam by signing up for free. Bank Exams: The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams
Description
Full syllabus notes, lecture & questions for The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams - Bank Exams | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude for Competitive Examinations | Best notes, free PDF download
Information about Chapter Notes: The Chain Rule
In this doc you can find the meaning of Chapter Notes: The Chain Rule defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: The Chain Rule theory, EduRev gives you an ample number of questions to practice Chapter Notes: The Chain Rule tests, examples and also practice Bank Exams
tests
Related Searches
Extra Questions
,Exam
,mock tests for examination
,past year papers
,ppt
,The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams
,Summary
,MCQs
,The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams
,Previous Year Questions with Solutions
,practice quizzes
,study material
,video lectures
,Viva Questions
,Sample Paper
,shortcuts and tricks
,Free
,Objective type Questions
,The Chain Rule Chapter Notes | Quantitative Aptitude for Competitive Examinations - Bank Exams
,Semester Notes
,Important questions
;
Additional Information about Chapter Notes: The Chain Rule for Bank Exams Preparation
Chapter Notes: The Chain Rule Free PDF Download
The Chapter Notes: The Chain Rule is an invaluable resource that delves deep into the core of the Bank Exams exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: The Chain Rule now and kickstart your journey towards success in the Bank Exams exam.
Importance of Chapter Notes: The Chain Rule
The importance of Chapter Notes: The Chain Rule cannot be overstated, especially for Bank Exams aspirants.
This document holds the key to success in the Bank Exams exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: The Chain Rule
Chapter Notes: The Chain Rule Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: The Chain Rule.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: The Chain Rule Notes on EduRev are your ultimate resource for success.
Chapter Notes: The Chain Rule Bank Exams Questions
The "Chapter Notes: The Chain Rule Bank Exams Questions" guide is a valuable resource for all aspiring students preparing for the
Bank Exams exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: The Chain Rule on the App
Students of Bank Exams can study Chapter Notes: The Chain Rule alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: The Chain Rule,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: The Chain Rule is prepared as per the latest Bank Exams syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily