The Product Rule Chapter Notes | Calculus AB - Grade 9 PDF Download
| Table of contents |
|
| Understanding the Product Rule |
|
| Applying the Product Rule: A Step-by-Step Example |
|
| Practice Problems to Solidify Your Skills |
|
| Why the Product Rule Matters |
|
Welcome to another dive into AP Calculus! Today, we’re tackling the Product Rule, a crucial tool for finding the derivative of a product of two functions. Building on your knowledge of derivatives at a point, sum and difference rules, and trigonometric derivatives, let’s sharpen your skills with this essential concept.
Understanding the Product Rule
When you need to differentiate a function that’s the product of two functions, say f(x) and g(x), the Product Rule comes to the rescue. It states that the derivative of the product is the first function times the derivative of the second, plus the second function times the derivative of the first.
Mathematically, this is expressed as:
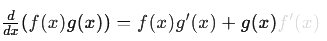
A handy mnemonic to remember this is: “First times derivative of the second, plus second times derivative of the first.” This rule is necessary because the derivative of a product is not simply the product of the derivatives.
Applying the Product Rule: A Step-by-Step Example
Let’s find the derivative of the function f(x) = sin(x)(x² + 2x).
Using the Product Rule:
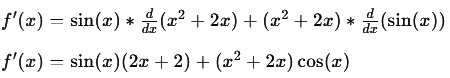
If we incorrectly attempt to calculate the derivative of $f(x)$, it would say
f′(x) = cos(x)(2x + 2)
However, sin(x)(2x + 2) + (x2+2x)cos(x) ≠ cos(x)(2x + 2).
This can be seen in the following graphs. f′(x) represents the correct derivative of $f(x)$ because the critical points and positive and negative values match the original functions.
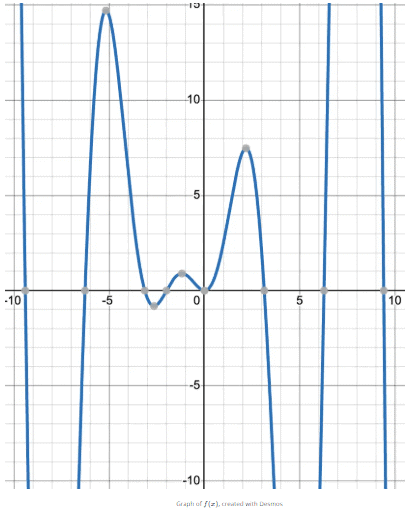
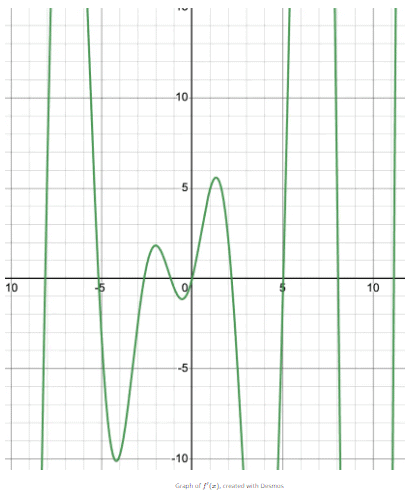
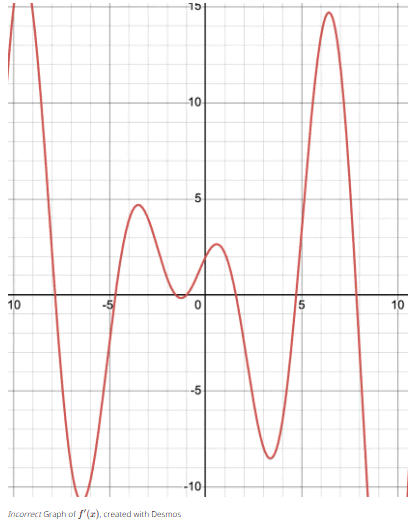
Practice Problems to Solidify Your Skills
Let’s work through some examples to master the Product Rule.
Example 1: Differentiating y = (3x² − 4x)(2x − 1) with and without the Product Rule.
Solving Example 1 Without Product Rule
First, expand the function:
y = (3x² − 4x)(2x − 1) = 6x³ − 3x² − 8x² + 4x = 6x³ − 11x² + 4x
Now, apply the sum rule to differentiate:
y' = 18x² − 22x + 4
With the Product Rule:
Apply the formula directly:
y' = (3x² − 4x) * d/dx(2x − 1) + (2x − 1) * d/dx(3x² − 4x)
Derivatives: d/dx(2x − 1) = 2 and d/dx(3x² − 4x) = 6x − 4.
So:
y' = (3x² − 4x)(2) + (2x − 1)(6x − 4)
For the AP Calculus exam, simplification isn’t always required, so this form is acceptable.
Example 2: Differentiating f(x) = sin(x)(3x² − 2x + 5)
Using the Product Rule:
f'(x) = sin(x) * d/dx(3x² − 2x + 5) + (3x² − 2x + 5) * d/dx(sin(x))
Derivatives: d/dx(3x² − 2x + 5) = 6x − 2 and (d/dx)(sin(x)) = cos(x).
Thus: f'(x) = sin(x)(6x − 2) + (3x² − 2x + 5)cos(x)
Tip: Review trigonometric derivatives, like d/dx(sin(x)) = cos(x), to stay sharp!
Example 3: Differentiating y′ if y = ex sin(x)
Remember that the derivative of ex is still ex! Now we can use the product rule.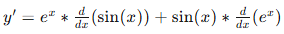
Therefore,
y′ = ex cos(x) + ex sin(x)
Why the Product Rule Matters
The Product Rule is a cornerstone of AP Calculus, frequently appearing in both multiple-choice and free-response questions. Mastering it will prepare you for more complex differentiation techniques, like the Chain Rule, and ensure you can handle a variety of functions on the exam.
Key Terms to Know
- Chain Rule: A method for differentiating composite functions, where the derivative is the outer function’s derivative times the inner function’s derivative.
- Cos x: The cosine function, representing the x-coordinate on the unit circle for a given angle, or the adjacent-to-hypotenuse ratio in a right triangle.
- Ex: The exponential function with base e (≈2.71828), modeling continuous growth or decay.
- G'(x): The derivative of g(x), indicating the rate of change or slope of the tangent line at a point.
- (f(x) * g(x))': The derivative of the product of two functions, found using the Product Rule.
- Ln x: The natural logarithm, the inverse of ex, giving the exponent needed to produce x with base e.
- Ln(x+2): The natural logarithm giving the exponent to which e must be raised to get x+2.
- Product Rule: A formula for differentiating the product of two functions: first times derivative of second, plus second times derivative of first.
- Sin x: The sine function, representing the opposite-to-hypotenuse ratio in a right triangle or the y-coordinate on the unit circle.
- Sin(x²): The sine of x squared, applying the sine function to the square of x.
|
26 videos|75 docs|38 tests
|
Exam
,Previous Year Questions with Solutions
,Free
,shortcuts and tricks
,video lectures
,Semester Notes
,ppt
,The Product Rule Chapter Notes | Calculus AB - Grade 9
,Sample Paper
,Viva Questions
,The Product Rule Chapter Notes | Calculus AB - Grade 9
,mock tests for examination
,MCQs
,The Product Rule Chapter Notes | Calculus AB - Grade 9
,past year papers
,Objective type Questions
,Important questions
,study material
,Summary
,practice quizzes
,Extra Questions
;
Chapter Notes: The Product Rule Free PDF Download
Importance of Chapter Notes: The Product Rule
Chapter Notes: The Product Rule
Chapter Notes: The Product Rule Grade 9 Questions
Study Chapter Notes: The Product Rule on the App
|
© EduRev
|
Education Revolution
|
|
