Three-dimensional Shapes Chapter Notes | Mathematics Class 6 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Components of a 3D Shape |

|
| Polyhedrons |

|
| 3D Shapes with Curved Face |

|
| Nets of 3D Shapes |

|
| Visualizing Solid Objects |

|
Introduction
Imagine the world around you—everything from a tiny thread to a massive wardrobe has a shape! Some objects, like a single strand of hair, only stretch in one direction (length). Others, like a piece of paper, spread out in two directions (length and breadth). But the most fascinating ones, like a box or a ball, take up space in three directions—length, breadth, and height. These are called three-dimensional (3D) shapes, and they’re all around us in our daily lives, from the juice can you drink from to the dice you roll in a game. In this chapter, we’ll dive into the exciting world of 3D shapes, exploring their parts, types, and how they can be unfolded or viewed from different angles. Get ready to see the world in a whole new dimension!
Classification of Objects: 1D, 2D, and 3D
- Objects are classified based on the dimensions they occupy.
- One-dimensional (1D): Objects with only length, like a thread or a hair.
- Two-dimensional (2D): Objects with length and breadth, like a sheet of paper.
- Three-dimensional (3D): Objects with length, breadth, and height, like a wardrobe or a box.
- 3D shapes are the focus of this chapter, as they have volume and take up space in all three directions.
Example: A thread is 1D (only length), a piece of paper is 2D (length and breadth), and an almirah is 3D (length, breadth, and height).
Components of a 3D Shape
- 3D shapes have three main parts: faces, edges, and vertices.
- Face (F): A flat or curved surface of a 3D shape.
- Edge (E): The line where two faces meet.
- Vertex (V): The point where two or more edges intersect, also called a corner.
Example: A cube has 6 faces (all squares), 12 edges (where the squares meet), and 8 vertices (corners where edges intersect).
Polyhedrons
- A polyhedron is a 3D shape made up of flat polygonal faces.
- Polygons are 2D shapes with straight sides, like triangles or squares.
- Polyhedrons have only flat faces, no curved surfaces.
Example: A cuboid is a polyhedron with six rectangular faces.
Cuboid
- A cuboid is a 3D shape with six rectangular faces.
- All faces are rectangles, and opposite faces are equal in size.
- It has 6 faces, 12 edges, and 8 vertices.
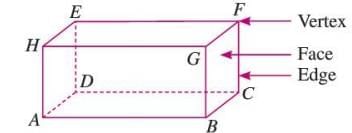
Example: A book is a real-life example of a cuboid, with rectangular faces of equal size on opposite sides.
Cube
- A cube is a special cuboid where all six faces are identical squares.
- It has 6 faces, 12 edges, and 8 vertices.
- All edges are of equal length.
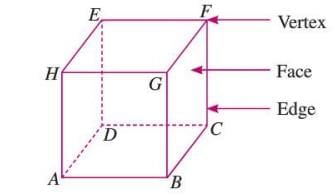
Example: A die used in board games is a cube, with all faces being squares of the same size.
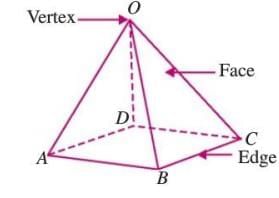
Pyramid
- A pyramid is a polyhedron with a polygonal base and triangular side faces that meet at a common point called the apex.
- The base can be any polygon, like a square or triangle.
- The side faces are always triangles.
Example: A square pyramid has a square base and four triangular side faces meeting at the apex.
Square Pyramid
- A pyramid with a square base is called a square pyramid.
- It has 5 faces (1 square base and 4 triangular side faces), 8 edges, and 5 vertices.
Example: The Great Pyramid of Giza is an example of a square pyramid.
Triangular Pyramid or Tetrahedron
- A pyramid with a triangular base is called a triangular pyramid or tetrahedron.
- It has 4 faces (all triangles), 6 edges, and 4 vertices.
- All faces are triangular and equal in a regular tetrahedron.
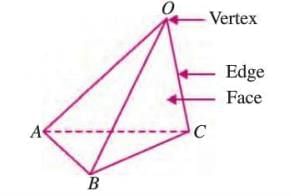
Example: A tetrahedron can be seen in some molecular structures, like methane, where atoms form a triangular pyramid shape.
Prism
- A prism is a polyhedron with two parallel, congruent polygonal bases connected by parallelogram side faces.
- The bases can be any polygon, like triangles or squares.
- The side faces are parallelograms.
Example: A triangular prism has two triangular bases and three parallelogram side faces.
Triangular Prism
- A prism with triangular bases is called a triangular prism.
- It has 5 faces (2 triangular bases and 3 rectangular side faces), 9 edges, and 6 vertices.
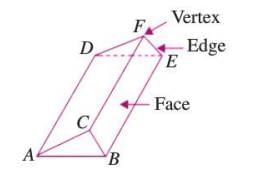
Example: A camping tent often resembles a triangular prism, with two triangular ends and rectangular sides.
3D Shapes with Curved Face
- Some 3D shapes have curved surfaces instead of flat polygonal faces.
- These include spheres, cones, and cylinders.
Example: A sphere, like a tennis ball, has a single curved surface.
Sphere
- A sphere is a 3D shape where every point on the surface is equidistant from its center.
- It has 1 curved face, 0 edges, and 0 vertices.
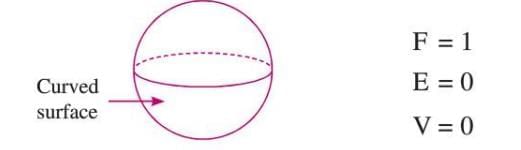
- Formula:
- Surface Area = 4πr2 (where r is the radius).
- Volume = (4/3)πr3.
Example: A tennis ball is a sphere, with all points on its surface equally distant from its center.
Cone
- A cone is a 3D shape with a single circular base that tapers to a point called the apex.
- It has 1 curved face, 1 flat circular base, 1 edge, and 1 vertex.
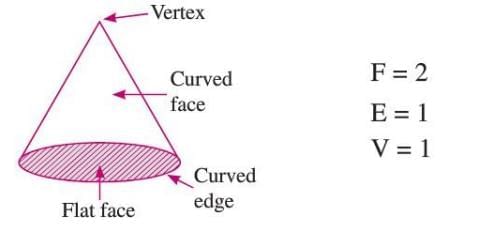
- Formula:
- Curved Surface Area = πrl (where r is the radius of the base, l is the slant height).
- Total Surface Area = πr(r + l).
- Volume = (1/3)πr2h (where h is the height).
Example: An ice cream cone is a real-life example, with a circular base and a single vertex at the top.
Cylinder
- A cylinder is a 3D shape with two parallel circular bases connected by a curved surface.
- It has 1 curved face, 2 flat circular faces, and 2 edges.

- Formula:
- Curved Surface Area = 2πrh (where r is the radius, h is the height).
- Total Surface Area = 2πr(r + h).
- Volume = πr2h.
Example: A can of soda is a cylinder, with two circular bases and a curved surface connecting them.
Nets of 3D Shapes
- A net is a 2D shape that can be folded to form a 3D shape.
- It is like the unfolded "skeleton" of a 3D object.
- Not all 3D shapes have nets (e.g., a sphere does not have a net).
Example: When a cardboard box (cuboid) is cut along its edges and laid flat, it forms a net that can be folded back into the box.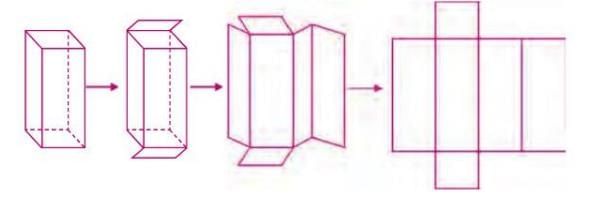
Nets of Various 3D Shapes
Cube
- A cube’s net consists of 6 squares arranged in a specific pattern.
- Common arrangements include a cross pattern or a 2x3 grid of squares.
Example: A net of a cube can be 6 squares arranged in a cross shape, which can be folded to form the cube.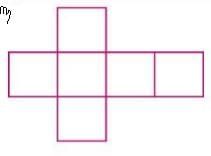
Cuboid
- A cuboid’s net consists of 6 rectangles arranged to form the shape when folded.
- The rectangles are arranged to match the cuboid’s dimensions (length, breadth, height).
Example: A cuboid’s net might have 4 rectangles in a row and 2 additional rectangles attached to the sides, forming a cross.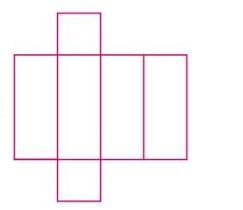
Cylinder
- A cylinder’s net includes 2 circles (for the bases) and a curved rectangle (for the curved surface).
- The rectangle’s length equals the circumference of the base (2πr).
Example: A cylinder’s net has two circles and a rectangle that wraps around to form the curved surface.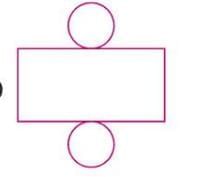
Cone
- A cone’s net consists of 1 circle (for the base) and a sector of a larger circle (for the curved surface).
- The sector’s arc length equals the circumference of the base (2πr).
Example: A cone’s net includes a circle and a sector that, when folded, forms the cone’s curved surface.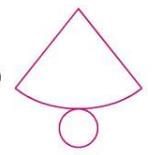
Triangular Pyramid or Tetrahedron
- A tetrahedron’s net consists of 4 triangles arranged so that they fold to form a pyramid with a triangular base.
- The triangles must be arranged to share edges correctly.
Example: A tetrahedron’s net might have 4 triangles arranged in a star pattern, folding to form the shape.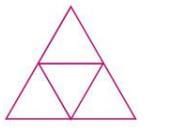
Visualizing Solid Objects
- Visualizing a 3D shape means imagining how it looks from different angles: front, side, or top.
- Not all parts of a 3D shape are visible from one angle, especially in combined shapes where some parts may be hidden.
- Different views (front, side, top) show different aspects of the shape.
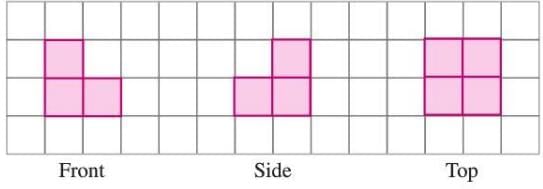
Example: A structure made of 7 cubes, when viewed from the front, side, or top, shows different arrangements of squares on a grid, depending on the perspective.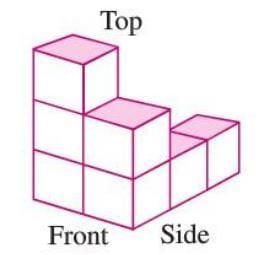
Solved Examples
Example 1: For the solids given below, sketch the front, side, and top views.
(a) A stack of cubes:
- Front view: Shows the height and width of the stack as a grid of squares.
- Side view: Shows the height and depth, with fewer squares visible.
- Top view: Shows the width and depth, forming a square or rectangular grid.
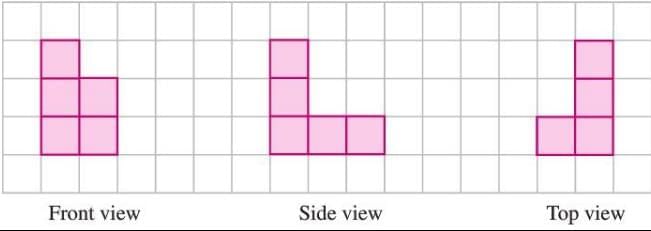
(b) A complex solid (e.g., combined cubes):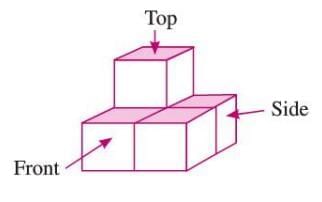
- Front view: Displays the visible faces from the front.
- Side view: Shows the profile from the side, possibly hiding some cubes.
- Top view: Shows the arrangement of cubes from above.
|
44 videos|202 docs|24 tests
|
FAQs on Three-dimensional Shapes Chapter Notes - Mathematics Class 6 ICSE
| 1. What are the main components of a 3D shape? |  |
| 2. What is a polyhedron and can you give some examples? |  |
| 3. How do 3D shapes with curved faces differ from polyhedrons? |  |
| 4. What is a net of a 3D shape, and why is it useful? |  |
| 5. How can one visualize solid objects effectively? |  |




















