Trigonometry Chapter Notes | Mathematics for Grade 10 PDF Download
Introducing the Roof Pitch Situation
The roof pitch situation provides a practical context for understanding trigonometry, focusing on how roof steepness is measured.Roof Pitch
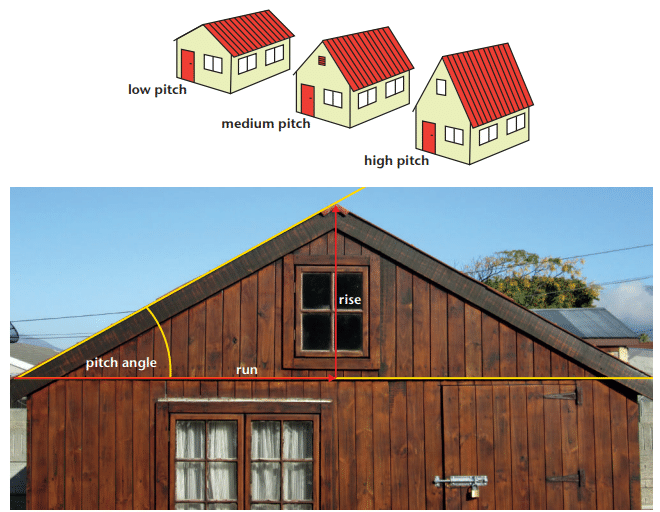
Definition: Roof pitch describes the steepness of a roof, measured as:
- An angle (in degrees or radians).
- A slope (rise:run ratio, dimensionless).
Key Question: How to convert between pitch angle and rise:run ratio? This is addressed throughout the chapter using trigonometric functions.
Example: A roof’s pitch can be expressed as a 30° angle or a rise:run ratio of 0,58 (derived later using tangent).
Revision of Angles, Lengths, Length Ratios, and Similarity
This section revises foundational concepts essential for trigonometry, emphasizing angles, lengths, and ratios in similar figures.Comparing Angles and Lengths
- Angles: Measured in degrees, representing the direction change between two paths.
- Lengths: Distances along paths or between points.
Example: Muvhuso at position O observes friends A, B, C, D moving from point M:
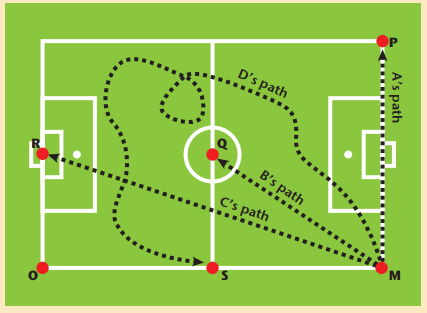
- C is furthest from M.
- B covers the shortest distance.
- A and B move through the same angle.
- C’s direction changes by 90°.
- D’s path is longest, but his angle change is 0°.
Length Ratios
Definition: A ratio compares two measurements, showing how many times one is larger or smaller than the other (dimensionless).
Example: Beams P (8,75 m) and Q (6,25 m):
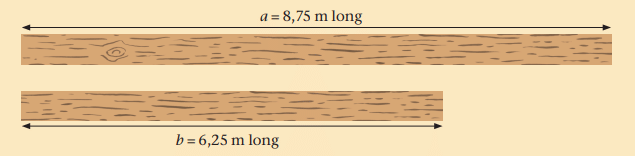
- Ratio P:Q = 8,75:6,25.
- Simplified: Divide by 0,25 → 35:25; divide by 5 → 7:5.
- Rational form: 8,75 ÷ 6,25 = 7/5 = 1,4 (P is 1,4 times longer than Q).
- Reciprocal (Q:P): 6,25 ÷ 8,75 = 5/7 ≈ 0,71.
- Difference: P is 2,50 m longer (not a ratio).
Similarity in Right-Angled Triangles
Concept: Similar triangles have equal angles and proportional corresponding sides.
Roof Pitch Context: Yellow triangles on a gable-end roof are similar, with hypotenuses along the roof slope, horizontal runs, and vertical rises.

- Pitch Angle: Equal across similar triangles.
- Side Lengths: Vary, but ratios (rise:run, rise:rafter, run:rafter) are constant.
Projections: Triangles are projections of each other, maintaining parallel sides and equal angles.
Ratios as Multipliers
- Example: If rise:run = 0,67, a 10 cm run gives a 6,7 cm rise (0,67 × 10). For a 25 cm run, rise = 16,75 cm.
Switching Between Pitch Angles and Roof Length Ratios with Sine, Cosine, and Tangent Functions
Trigonometric functions link pitch angles to side ratios in right-angled triangles, enabling conversions between angles and ratios.Trigonometric Functions
- Sine (sin): sin(pitch angle) = rise length ÷ rafter length.
- Cosine (cos): cos(pitch angle) = run length ÷ rafter length.
- Tangent (tan): tan(pitch angle) = rise length ÷ run length (pitch ratio).
Calculating Values
Given Pitch Angle and One Length:- Use sin or tan to find other lengths.
- Example: If pitch angle = 40°, sin 40° ≈ 0,64, cos 40° ≈ 0,77, tan 40° ≈ 0,84.
Given Lengths:
- Use inverse functions (sin⁻¹, cos⁻¹, tan⁻¹) to find the pitch angle.
- Example: Rise:run = 2:7 = 0,29 → tan⁻¹(0,29) ≈ 16°.
Scale Drawing Example
Problem: Find sin 40°, cos 40°, tan 40° by construction.- Draw a right-angled triangle with a 40° angle.
- Measure sides: rise (MN), run (OM), rafter (ON).
- Ratios: MN:ON = sin 40° ≈ 0,64; OM:ON = cos 40° ≈ 0,77; MN:OM = tan 40° ≈ 0,84.
Inverse Problem: Rise:run = 2:7, find angle.
- Construct triangle with run = 10 cm, rise = 2,9 cm.
- Measure angle ≈ 16°, confirm with tan⁻¹(2/7) ≈ 16°.
Calculator Use
- Ensure calculator is in degree mode (displays ‘D’).
- Use sin, cos, tan buttons for ratios; sin⁻¹, cos⁻¹, tan⁻¹ for angles.
Right-Angled Triangles
This section generalizes trigonometric functions to any right-angled triangle, introducing standard side naming conventions.Side Naming Conventions
- Hypotenuse (hyp): Opposite the right angle, longest side.
- Opposite (opp): Opposite the reference acute angle.
- Adjacent (adj): Next to the reference angle, forming one arm of the angle.
- Example: For angle α, opp is opposite α, adj is next to α, hyp is opposite the right angle.
Why Right-Angled Triangles?
- Simplest for angle-ratio relationships (e.g., Pythagorean Theorem).
- Non-right-angled triangles and polygons can be divided into right-angled triangles.
Example
Triangle ABC with ∠B = 90°, ∠A = 36°, AB = 15 cm:
- Hypotenuse: AC.
- Opposite to ∠A: BC.
- Adjacent to ∠A: AB.
- ∠C = 90° - 36° = 54°.
Defining the Trigonometric Functions
Formal definitions of trigonometric functions and their inverses are provided, along with reciprocal functions.
Basic Trigonometric Functions
- Sine: sin θ = opp ÷ hyp.
- Cosine: cos θ = adj ÷ hyp.
- Tangent: tan θ = opp ÷ adj.
- Mnemonic: SOH CAH TOA (Sine = Opp/Hyp, Cosine = Adj/Hyp, Tangent = Opp/Adj).
Inverse Trigonometric Functions
- Sine Inverse: θ = sin⁻¹(opp ÷ hyp).
- Cosine Inverse: θ = cos⁻¹(adj ÷ hyp).
- Tangent Inverse: θ = tan⁻¹(opp ÷ adj).
- Notation: sin⁻¹, cos⁻¹, tan⁻¹ (equivalent to arcsin, arccos, arctan).
Reciprocal Trigonometric Functions
- Cosecant: csc θ = hyp ÷ opp = 1 ÷ sin θ.
- Secant: sec θ = hyp ÷ adj = 1 ÷ cos θ.
- Cotangent: cot θ = adj ÷ opp = 1 ÷ tan θ.
- Example: csc 23° = 1 ÷ sin 23° ≈ 2,56.
Calculations
Example: For a triangle with opp = 7,23, hyp = p, θ = 35,7°:
- sin 35,7° = 7,23 ÷ p → p = 7,23 ÷ sin 35,7° ≈ 12,39.
- tan 35,7° = 7,23 ÷ adj → adj = 7,23 ÷ tan 35,7° ≈ 10,06.
- Or use Pythagorean Theorem: adj = √(12,39² - 7,23²) ≈ 10,06.
Complex Expressions
Example: Calculate (cos(2 × 30° - 12°)) ÷ (3 tan 21,4° + 0,5):
- Numerator: cos(60° - 12°) = cos 48° ≈ 0,669.
- Denominator: 3 tan 21,4° + 0,5 ≈ 1,176 + 0,5 = 1,676.
- Result: 0,669 ÷ 1,676 ≈ 0,40.
Input Angles of 0° and 90°
Special cases of 0° and 90° are explored, where standard triangle definitions may not apply.Challenges
A right-angled triangle cannot have acute angles of 0° or 90° (sum of acute angles must be 90°).Horizontal Roof (0°):
- Pitch angle = 0°.
- Rise:run = 0 (no rise).
- tan 0° = 0.
Vertical Wall (90°):
- Pitch angle = 90°.
- Rise:run is undefined (run = 0).
- tan 90° is undefined.
Implications: Trigonometric functions need alternative definitions (e.g., Cartesian) to handle 0° and 90°.
The Cartesian Grid: Looking at the Tangent Function in a Different Way
The Cartesian plane extends trigonometric definitions beyond right-angled triangles, using coordinates.Cartesian Representation
- Setup: Place the pitch angle vertex at the origin, runs along the x-axis, rises parallel to the y-axis.
- Coordinates: For a point P(x, y), r = √(x² + y²) is the radial distance from the origin.
- Tangent: tan θ = y ÷ x.
- Example: For points A, B, C, calculate y/x ratios, which match tan θ from triangle definitions.
Special Cases
- θ = 0°: Point on positive x-axis (y = 0), tan 0° = 0 ÷ x = 0.
- θ = 90°: Point on positive y-axis (x = 0), tan 90° = y ÷ 0 (undefined).
Angle Measurement
- Convention: Measure angles anticlockwise from the positive x-axis.
- Example: Positive x-axis (0°), positive y-axis (90°), negative x-axis (180°), negative y-axis (270°).
More Applications of Trigonometric Functions in the Cartesian Plane
Trigonometric functions are redefined using Cartesian coordinates, covering all angles from 0° to 360°.Cartesian Definitions
- Sine: sin θ = y ÷ r.
- Cosine: cos θ = x ÷ r.
- Tangent: tan θ = y ÷ x (undefined when x = 0, i.e., θ = 90°, 270°).
- r: Always positive, r = √(x² + y²).
Properties
Sine:
- Domain: 0° ≤ θ ≤ 360°.
- Range: -1 ≤ sin θ ≤ 1.
- Positive in quadrants 1, 2 (y > 0); negative in 3, 4 (y < 0).
- Zero on x-axis (y = 0); ±1 on y-axis (y = ±r, x = 0).
Cosine:
- Domain: 0° ≤ θ ≤ 360°.
- Range: -1 ≤ cos θ ≤ 1.
- Positive in quadrants 1, 4 (x > 0); negative in 2, 3 (x < 0).
- Zero on y-axis (x = 0); ±1 on x-axis (x = ±r, y = 0).
Tangent:
- Domain: 0° ≤ θ ≤ 360°, except θ = 90°, 270°.
- Range: All real numbers.
- Positive in quadrants 1, 3; negative in 2, 4.
- Zero on x-axis; undefined on y-axis.
Example
- Horizontal Roof: sin 0° = 0 ÷ r = 0, cos 0° = r ÷ r = 1.
- Vertical Wall: sin 90° = r ÷ r = 1, cos 90° = 0 ÷ r = 0.
Solving Trigonometric Equations
Trigonometric equations are solved to find angles within a specified domain.Examples
1. 2 tan x = 7:
- tan x = 7 ÷ 2 = 3,5.
- x = tan⁻¹(3,5) ≈ 74,1°.
2. 3 sin x = 4:
- sin x = 4 ÷ 3 ≈ 1,33 (invalid, as sin x ≤ 1).
- No solution.
Complex Equations
(2 sin(θ - 10°) + 0,2) ÷ 3 = 0,27:
- 2 sin(θ - 10°) + 0,2 = 0,81.
- 2 sin(θ - 10°) = 0,61.
- sin(θ - 10°) = 0,305.
- θ - 10° = sin⁻¹(0,305) ≈ 17,77°.
- θ ≈ 27,77°.
Practical Applications of Trigonometric Functions
Trigonometry is applied to real-world problems, such as measuring heights and distances.Examples
Tower Height: Distance = 100 m, angle of elevation = 35°.
- tan 35° = height ÷ 100.
- Height = 100 × tan 35° ≈ 70,02 m.
Kite Distance: String length = 800 m, angle = 35°.
- cos 35° = distance ÷ 800.
- Distance = 800 × cos 35° ≈ 655,32 m.
Graphs of Trigonometric Functions
Graphing trigonometric functions reveals their behavior and properties.Sine Graph (y = sin θ)

- Shape: Sinusoidal (wave-like).
- Turning Points: (90°, 1), (270°, -1).
- Amplitude: 1.
- Intercepts: (0°, 0), (180°, 0), (360°, 0).
- Behavior: Positive for 0° < θ < 180°, negative for 180° < θ < 360°.
Cosine Graph (y = cos θ)
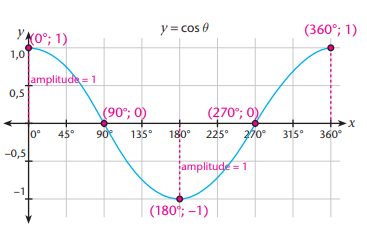
- Shape: Sinusoidal.
- Turning Points: (0°, 1), (180°, -1), (360°, 1).
- Amplitude: 1.
- Intercepts: (90°, 0), (270°, 0).
- Behavior: Positive for 0° < θ < 90°, 270° < θ < 360°; negative for 90° < θ < 270°.
Tangent Graph (y = tan θ)
- Shape: Curved with asymptotes at θ = 90°, 270°.
- Intercepts: (0°, 0), (180°, 0), (360°, 0).
- Behavior: Always increasing, positive in quadrants 1, 3; negative in 2, 4.
- Asymptotes: Vertical lines at θ = 90°, 270° (tan θ undefined).
Transformations
- Dilation/Contraction: y = a sin θ; a > 1 dilates, 0 < a < 1 contracts.
- Reflection: y = -sin θ reflects over θ-axis.
- Translation: y = sin θ + q; q > 0 shifts up, q < 0 shifts down.
- Example: y = 2 sin θ doubles amplitude, y = sin θ + 2 shifts up by 2 units.
Notation
- Function Labels: e.g., h(θ) = 1/4 sin θ.
- Output: h(41°) = 1/4 sin 41° ≈ 0,164.
- Graphing: Plot (θ, h(θ)) pairs.
Points to Remember
- Trigonometric Functions: Relate angles to side ratios in right-angled triangles (sin θ = opp ÷ hyp, cos θ = adj ÷ hyp, tan θ = opp ÷ adj).
- Inverse Functions: Find angles from ratios (e.g., θ = sin⁻¹(opp ÷ hyp)).
- Reciprocal Functions: csc θ = 1 ÷ sin θ, sec θ = 1 ÷ cos θ, cot θ = 1 ÷ tan θ.
- Cartesian Definitions: sin θ = y ÷ r, cos θ = x ÷ r, tan θ = y ÷ x; r = √(x² + y²).
- Domains and Ranges:
Sine/Cosine: Domain 0° ≤ θ ≤ 360°, Range [-1, 1].
Tangent: Domain 0° ≤ θ ≤ 360° (except 90°, 270°), Range all real numbers. - Graph Properties:
Sine/Cosine: Sinusoidal, amplitude 1, specific turning points and intercepts.
Tangent: Asymptotes at 90°, 270°, always increasing. - Transformations: Coefficients affect dilation, contraction, reflection; constants cause vertical shifts.
- Applications: Solve for sides, angles, and ratios in right-angled triangles; apply to practical problems like height measurement.
- Special Angles: tan 0° = 0, tan 90° undefined.
Fascinating Facts:
- Corresponding sides of similar right-angled triangles have constant ratios.
- Trigonometric functions link angles to side ratios in triangles and coordinates in the Cartesian plane.
- Right-angled triangles simplify trigonometric calculations and can represent parts of any polygon.
- Sine and cosine graphs are congruent, shifted along the θ-axis, used in wave modeling (e.g., sound, electricity).
- Tangent’s undefined values at 90°, 270° create asymptotes in its graph.
Difficult Words
- Trigonometry: The study of relationships between angles and side ratios in triangles.
- Pitch: The steepness of a roof, measured as an angle or rise:run ratio.
- Ratio: A comparison of two quantities, dimensionless (e.g., 7:5).
- Hypotenuse: The longest side of a right-angled triangle, opposite the right angle.
- Opposite: The side opposite a specified angle in a triangle.
- Adjacent: The side next to a specified angle, forming one arm of the angle.
- Sine (sin): A function giving the ratio opp ÷ hyp.
- Cosine (cos): A function giving the ratio adj ÷ hyp.
- Tangent (tan): A function giving the ratio opp ÷ adj.
- Inverse Function: A function that reverses the input-output relationship (e.g., sin⁻¹ finds angle from ratio).
- Cosecant (csc): Reciprocal of sine, hyp ÷ opp.
- Secant (sec): Reciprocal of cosine, hyp ÷ adj.
- Cotangent (cot): Reciprocal of tangent, adj ÷ opp.
- Asymptote: A line that a graph approaches but never touches (e.g., θ = 90° for tan θ).
- Dilation: Stretching a graph (e.g., y = 2 sin θ).
- Contraction: Compressing a graph (e.g., y = 1/4 sin θ).
- Reflection: Flipping a graph over an axis (e.g., y = -sin θ).
- Translation: Shifting a graph vertically (e.g., y = sin θ + 2).
- Sinusoidal: A wave-like shape, characteristic of sine and cosine graphs.
Summary
The Trigonometry chapter equips Grade 10 students with tools to analyze angles and side ratios in right-angled triangles and the Cartesian plane, vital for technical applications like engineering and architecture. Students learn to use sine, cosine, and tangent functions to convert between pitch angles and roof length ratios, calculate unknown sides and angles, and solve practical problems like measuring tower heights. The chapter extends definitions to the Cartesian plane, covering angles from 0° to 360°, and explores graphing trigonometric functions, highlighting their sinusoidal shapes, asymptotes, and transformations. Reciprocal and inverse functions enhance problem-solving flexibility, while special cases (0°, 90°) are addressed using Cartesian coordinates. This comprehensive study empowers students to apply trigonometry effectively in real-world technical contexts.|
1 videos|57 docs|4 tests
|
FAQs on Trigonometry Chapter Notes - Mathematics for Grade 10
| 1. What is roof pitch, and how is it measured? |  |
| 2. How do sine, cosine, and tangent functions relate to roof pitch? |  |
| 3. How can I convert a roof pitch ratio into an angle? |  |
| 4. What are practical applications of trigonometric functions in real life? |  |
| 5. How do I solve basic trigonometric equations? |  |
















