Using L'Hopitals Rule for Determining Limits in Indeterminate Forms Chapter Notes | Calculus AB - Grade 9 PDF Download
| Table of contents |

|
| What is L'Hôpital's Rule? |

|
| Applying L'Hôpital's Rule: A Step-by-Step Example |

|
| Practice Problems for L'Hôpital's Rule |

|
| Solutions to Practice Problems |

|
| Conclusion |

|
From earlier studies, you might remember that certain limits of functions result in indeterminate forms like 0/0 or ±∞/∞. These forms are ambiguous and cannot be evaluated directly. Instead of manipulating the expression algebraically to resolve the indeterminacy, we can use a powerful tool called L'Hôpital's Rule, which leverages derivatives to simplify the process.
What is L'Hôpital's Rule?
L'Hôpital's Rule provides a method to evaluate limits of indeterminate forms. Specifically, it applies when:
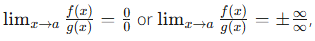
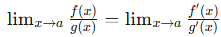
Basically, the rule states that we can evaluate the limits of indeterminate forms using their derivatives!
This means you can find the limit by taking the derivatives of the numerator and denominator separately and then evaluating the new limit. Note that L'Hôpital's Rule is distinct from the quotient rule for derivatives and is only applicable to these specific indeterminate limit cases.
Applying L'Hôpital's Rule: A Step-by-Step Example
Let's evaluate the following limit:
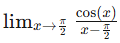
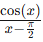
This is an indeterminate form, so L'Hôpital's Rule is appropriate. First, verify the conditions by checking the limits of the numerator and denominator:
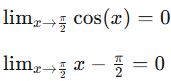
Since 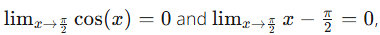 L’Hopital’s Rule can be applied. Be sure to write this statement out before actually applying this rule.
L’Hopital’s Rule can be applied. Be sure to write this statement out before actually applying this rule.
Now, we can take the derivatives and get into L’Hopital’s Rule.
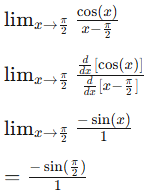
In conclusion, we know that this limit…
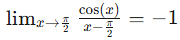
Practice Problems for L'Hôpital's Rule
Test your understanding with these practice problems, treating them as free-response questions where you must verify the conditions for L'Hôpital's Rule.
Question 1
limx→0 tan(x)/(7x + tan(x))
Question 2
limx→∞ (3x² - 8)/(7x² + 21)
Solutions to Practice Problems
Question 1 Solution
Plugging x = 0 into
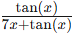 results in the indeterminate form 0/0. Since the expression involves mixed function types, it is not possible to manipulate it algebraically in any way to find the limits. Therefore, we should use L’Hopital’s Rule.
results in the indeterminate form 0/0. Since the expression involves mixed function types, it is not possible to manipulate it algebraically in any way to find the limits. Therefore, we should use L’Hopital’s Rule.But first, show that the limits are separately equal to 0.
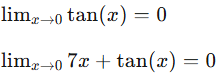
Since
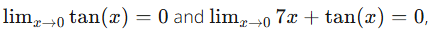 L’Hopital’s Rule can be applied.
L’Hopital’s Rule can be applied.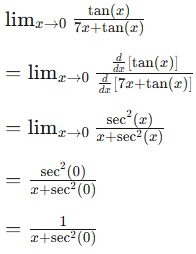
In conclusion…
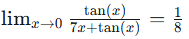
Question 2 Solution
Plugging x = ∞ into 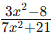 results in the indeterminate form
results in the indeterminate form 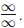 Therefore, we should use L’Hopital’s Rule.
Therefore, we should use L’Hopital’s Rule.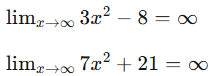
Since 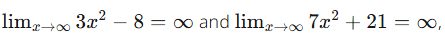 L’Hopital’s Rule can be applied.
L’Hopital’s Rule can be applied.
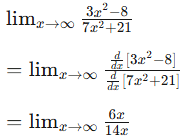
Therefore…
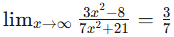
Key Terms to Understand
- Indeterminate Forms: These are expressions that yield ambiguous or undefined values, such as 0/0 or ∞/∞, often encountered when computing limits.
- L'Hôpital's Rule: A technique for resolving indeterminate limits by taking the derivatives of the numerator and denominator, allowing for easier evaluation of the limit.
Conclusion
L'Hôpital's Rule is an efficient method for tackling limits that result in indeterminate forms. By applying derivatives, it simplifies complex problems, making limit evaluation more straightforward. Keep practicing, and happy calculus learning!
|
26 videos|75 docs|38 tests
|
FAQs on Using L'Hopitals Rule for Determining Limits in Indeterminate Forms Chapter Notes - Calculus AB - Grade 9
| 1. What is L'Hôpital's Rule and when can it be applied? |  |
| 2. How do you apply L'Hôpital's Rule step-by-step? |  |
| 3. Can L'Hôpital's Rule be applied more than once? |  |
| 4. What are some common indeterminate forms that L'Hôpital's Rule can be used for? |  |
| 5. Are there any limitations or conditions for using L'Hôpital's Rule? |  |



















