Volume and Capacity Chapter Notes | Mathematics Class 8 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Cuboid (A Rectangular Solid) |

|
| Cube |

|
| Application |

|
| Cylinder |

|
Introduction
This chapter introduces the concepts of volume, capacity, and surface area for three-dimensional shapes like cuboids, cubes, and cylinders. Volume refers to the space occupied by a solid, capacity is the internal volume of a container, and surface area is the total area of all faces of a solid. The following notes provide a clear, step-by-step explanation of each concept, accompanied by examples and practical applications that illustrate the calculations.
Key Points
- Volume is the measure of how much space an object occupies. It is usually measured in cubic units, such as cubic meters (m³), cubic centimeters (cm³), or liters (L). The formula to calculate the volume of a cuboid is:
Volume of a Cuboid = Length × Breadth × Height - Capacity refers to the maximum amount of space that a container can hold. It is often measured in litres or gallons. For example, a water tank with a capacity of 1000 litres can hold 1000 litres of water. The capacity of a cuboid can be calculated using the same formula as volume, since it refers to the space inside the container.
- Surface area is the total area of all the surfaces of a three-dimensional object. It is measured in square units, such as square meters (m²) or square centimetres (cm²). The formula to calculate the surface area of a cuboid is:
Surface Area of a Cuboid = 2 × (Length × Breadth + Length × Height + Breadth × Height)
Units of measurement:
- Length: metre (m), centimetre (cm), millimetre (mm).
- Volume: cubic metre (m³), cubic centimetre (cm³), cubic millimetre (mm³).
- Surface area: square metre (m²), square centimetre (cm²), square millimetre (mm²).
Conversion between units:
- 1 m³ = 1,000,000 cm³ (100 × 100 × 100 cm³).
- 1 cm³ = 1/1,000,000 m³.
- 1 cm³ = 1,000 mm³ (10 × 10 × 10 mm³).
- 1 mm³ = 1/1,000 cm³.
Volume of liquids or gases is measured in litres:
- 1 m³ = 1,000 litres.
- 1 litre = 1,000 cm³ (also called millilitres or c.c.).
Example: Understand that if a container has a capacity of 1 litre, its internal volume is 1,000 cm³.
Cuboid (A Rectangular Solid)
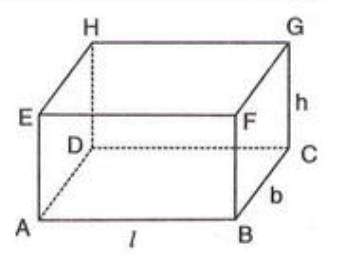
A cuboid is a solid shape with six rectangular faces.
Key measurements
- Volume: The volume of a cuboid is calculated by multiplying its length, breadth, and height. The formula is: Volume = Length × Breadth × Height (l × b × h).
- Total Surface Area: The total surface area of a cuboid is found by using the formula: Total Surface Area = 2(l × b + b × h + h × l).
Area of Faces
- Area of Top and Bottom Faces: The area of the top and bottom faces is calculated as 2(l × b).
- Area of Front and Back Faces: The area of the front and back faces is calculated as 2(b × h).
- Area of Left and Right Faces: The area of the left and right faces is calculated as 2(h × l).
Steps to calculate Volume
- To calculate the volume of a cuboid, measure the length, breadth, and height in the same unit.
- Multiply these three dimensions together: Volume = Length × Breadth × Height.
- Express the result in cubic units, such as cm³ or m³.
Steps to Calculate the Total Surface Area
- Measure the length, breadth, and height of the cuboid in the same unit.
- Calculate the following products: Length × Breadth, Breadth × Height, and Height × Length.
- Add these three products together and multiply the sum by 2.
Total Surface Area = 2 × (Length × Breadth + Breadth × Height + Height × Length). - Express the result in square units, such as cm² or m².
Example: A cuboid has length, breadth, and height in the ratio 6:5:4, with a volume of 15,000 cm³.
Steps to find dimensions:
- Let length = 6x cm, breadth = 5x cm, height = 4x cm.
- Volume = 6x × 5x × 4x = 15,000 cm³.
- Simplify: 120x³ = 15,000 → x³ = 15,000/120 = 125.
- Find x: x = ∛125 = 5.
- Dimensions: length = 6 × 5 = 30 cm, breadth = 5 × 5 = 25 cm, height = 4 × 5 = 20 cm.
Steps to find surface area:
- Use formula: 2(l × b + b × h + h × l).
- Substitute: 2(30 × 25 + 25 × 20 + 20 × 30) = 2(750 + 500 + 600) = 2 × 1850 = 3,700 cm².
Cube
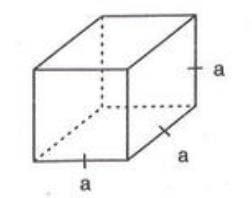
A cube is a special kind of cuboid where all the faces are squares, meaning the length, breadth, and height are all the same. Let's say the edge of the cube is a.
- Volume = a × a × a = a³ ( edge³ ).
- Total surface area = 6 × (edge)² = 6a² (since each face is a square).
Steps to calculate Volume
- Measure the edge length ( a ).
- Calculate the volume by finding a³.
- Express the result in cubic units.
Steps to calculate the Total Surface Area
- Measure the edge length (a).
- Calculate a² for one face.
- Multiply by 6 (since a cube has 6 faces).
- Express the result in square units.
Example:
- A cube has a total surface area of 294 cm². Find its volume.
- Steps:
- Total surface area = 6a² = 294 cm².
- Find a²: a² = 294/6 = 49.
- Find a: a = √49 = 7 cm.
- Volume = a³ = 7³ = 343 cm³.
Application
Application 1: For a Room
- A room has four walls: two along its length and two along its width.
- Area calculations:
- Area of each wall along length = length × height (l × h).
- Area of each wall along width = breadth × height (b × h).
- Total area of four walls = 2(l × h) + 2(b × h) = 2(l + b) × h.
- This includes the area of doors and windows.
- Area of roof = area of floor = length × breadth (l × b).
- Steps to calculate the area to be whitewashed:
- Calculate the area of four walls: 2(l + b) × h.
- Calculate the area of the roof: l × b.
- Subtract the area of doors and windows if they are not to be whitewashed.
- Add the remaining areas to get the total area to be whitewashed.
Example: A room has internal dimensions 6 m (length), 5.2 m (breadth), 4.5 m (height), with two doors (1.2 m × 2 m) and three windows (1 m × 0.8 m). Find the area to be whitewashed and cost at ₹6 per m².
Steps:
- Area of four walls = 2(6 + 5.2) × 4.5 = 2 × 11.2 × 4.5 = 100.8 m².
- Area of roof = 6 × 5.2 = 31.2 m².
- Area of two doors = 2 × (1.2 × 2) = 4.8 m².
- Area of three windows = 3 × (1 × 0.8) = 2.4 m².
- Total area to whitewash = (100.8 + 31.2) - (4.8 + 2.4) = 124.8 m².
- Cost = 124.8 × 6 = ₹748.80.
Application 2: For a Box
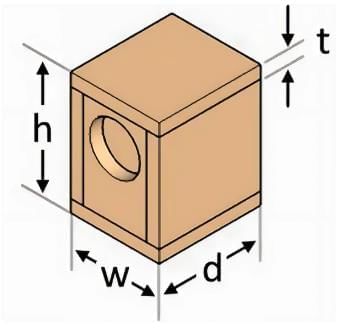
- Space occupied = external volume.
- Capacity = internal volume.
- Volume of material = external volume - internal volume.
- For a closed box with external dimensions l, b, h and wall thickness t:
- Internal length = l - 2t.
- Internal breadth = b - 2t.
- Internal height = h - 2t.
- If internal dimensions are l, b, h, and thickness is t:
- External length = l + 2t.
- External breadth = b + 2t.
- External height = h + 2t.
- Steps to calculate capacity:
- Find internal dimensions by subtracting twice the thickness from external dimensions.
- Calculate the internal volume: length × breadth × height
- Steps to calculate the volume of material:
- Calculate external volume: l × b × h.
- Calculate internal volume: (l - 2t) × (b - 2t) × (h - 2t).
- Subtract internal volume from external volume.
Example: A closed wooden box has external dimensions 30 cm, 18 cm, 20 cm, with walls 1.5 cm thick. Find capacity, volume of wood, and weight if 1 cm³ of wood weighs 0.8 g.
Steps:
- External volume = 30 × 18 × 20 = 10,800 cm³.
- Internal dimensions: length = 30 - 2 × 1.5 = 27 cm, breadth = 18 - 2 × 1.5 = 15 cm, height = 20 - 2 × 1.5 = 17 cm.
- Capacity (internal volume) = 27 × 15 × 17 = 6,885 cm³.
- Volume of wood = 10,800 - 6,885 = 3,915 cm³.
- Weight = 3,915 × 0.8 = 3,132 g = 3.132 kg.
Cylinder
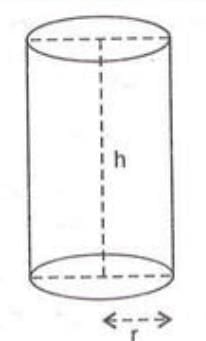
A cylinder is a solid with a uniform circular cross-section. Let the radius of the base = r cm, height = h cm.
Key measurements
- Area of cross-section = πr².
- Perimeter of cross-section = 2πr.
- Curved surface area = perimeter × height = 2πrh.
- Total surface area = curved surface area + 2 × area of cross-section = 2πrh + 2πr² = 2πr(h + r).
- Volume = area of cross-section × height = πr²h.
- Use π = 22/7 unless specified otherwise.
Steps to calculate Curved Surface Area
- Measure radius (r) and height (h).
- Calculate 2πrh.
- Express in square units.
Steps to calculate the Total Surface Area
- Calculate curved surface area: 2πrh.
- Calculate the area of two bases: 2 × πr².
- Add both: 2πr(h + r).
- Express in square units.
Steps to calculate Volume
- Measure radius (r) and height (h).
- Calculate πr²h.
- Express in cubic units.
Example:
- A cylinder has a curved surface area of 17,600 cm² and a base circumference of 220 cm. Find height and volume.
- Steps:
- Curved surface area = 2πrh = 17,600 cm², circumference = 2πr = 220 cm.
- Find height: h = 17,600 / 220 = 80 cm.
- Find radius: 2πr = 220 → 2 × 22/7 × r = 220 → r = (220 × 7) / (2 × 22) = 35 cm.
- Volume = πr²h = 22/7 × 35 × 35 × 80 = 308,000 cm³.
|
23 videos|122 docs|14 tests
|
FAQs on Volume and Capacity Chapter Notes - Mathematics Class 8 ICSE
| 1. What is the difference between a cuboid and a cube? |  |
| 2. How do you calculate the volume of a cuboid? |  |
| 3. What is the volume formula for a cube? |  |
| 4. In what real-life situations do we encounter cylinders, and how do we calculate their volume? |  |
| 5. How can we apply the concepts of volume and capacity in daily life? |  |















