Sometimes, we need to quickly and efficiently find missing numbers in sums or differences. In this section, we’ll learn how to do that with ease.
We the Travellers—II Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download

Introduction
By the end, you’ll see that maths is not just about numbers—it’s about smart shortcuts, exciting patterns, and solving everyday travel problems with ease. So, get ready for an exciting journey with numbers!
Making Sums Equal
Let’s Perform a Fun Exercise!
Two groups of numbers are waiting for you. Each group already has a total (sum).
But here’s the twist — their sums are not equal!
Your mission:
Swap numbers between the two groups.
Make sure both groups end up with the same sum.
Try to do it in the least number of moves (bonus points for just one clever swap).
Hint: Look carefully at the difference between the sums. The right swap will balance them perfectly!
Quick Tip: How to Find the Right Swap?
 View Answer
View Answer 
Step 1 – Find the difference
Subtract the smaller group’s sum from the larger group’s sum.
Step 2 – Look for a pair
Find one number from each group where their difference equals half of the total difference.
Step 3 – Swap them
Exchange these numbers and check the new sums.
They will now be equal!
Let's solve!
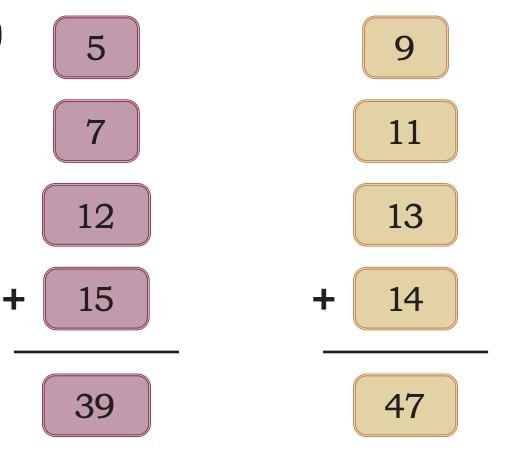
Group 1: 5, 7, 12, 15
→ Sum = 39Group 2: 9, 11, 13, 14
→ Sum = 47
Swap: 5 (Group 1) ↔ 9 (Group 2)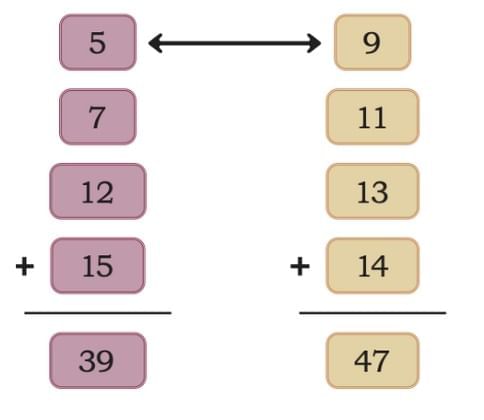
New Group 1: 9, 7, 12, 15 → Sum = 43
New Group 2: 5, 11, 13, 14 → Sum = 43
Fuel Arithmetic
Have you ever wondered how cars, bikes, and buses run? They need fuel! Just like we need food to get energy, vehicles need fuel to move. Different vehicles need different amounts of fuel.
- Motorbikes: Usually need a small amount, like 5 to 15 litres.
- Cars: Need a bit more, around 15 to 50 litres.
- Lorries and Trucks: These are big vehicles, so they need a lot more fuel, from 150 to 500 litres
- Trains:Imagine how big a train is! They need a huge amount, like 5,000 litre

Let's solve some problems related to fuel: Addition
A lorry has 28 litres of fuel in its tank. An additional 75 litres is filled. What is the total quantity of fuel in the lorry?
Solution:
To find the total quantity, we need to add the fuel already in the tank and the additional fuel filled.
Total quantity of fuel = 28 litres + 75 litres
Let's do it step-by-step:
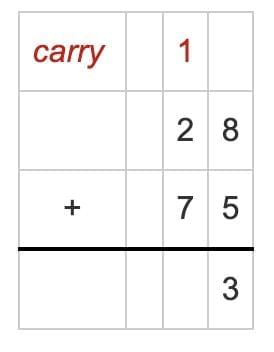
Step 1: Add the Ones place
8 (ones) + 5 (ones) = 13 ones.
13 ones = 1 ten and 3 ones.
Write 3 in the Ones place.
Carry over 1 ten to the Tens column.
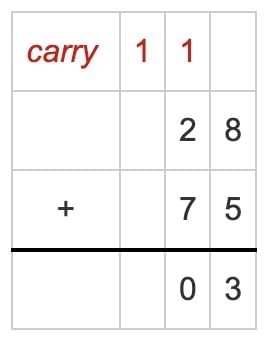
Step 2: Add the Tens place
Carried over 1 ten + 2 tens + 7 tens = 10 tens.
10 tens = 1 hundred and 0 tens.
Write 0 in the Tens place.
Carry over 1 hundred to the Hundreds column.
Step 3: Add the Hundreds place
Carried over 1 hundred + 0 = 1 hundred.
Write 1 in the Hundreds place.
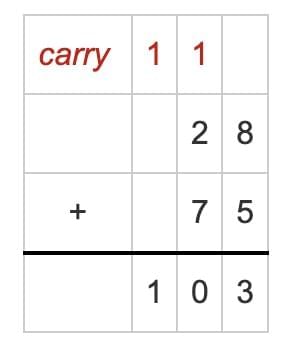
Final Answer = 103 litres
Relationship Between Addition and Subtraction
Addition and subtraction are linked.
Addition joins numbers to make a total.
Subtraction splits the total to find the missing part.
The same three numbers can make both addition and subtraction sentences
It’s as if one operation cancels out the other.
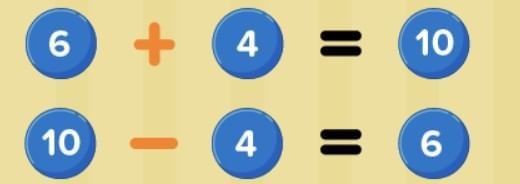
Let's understand this with the help of an example:
46 + 21 = 67
Here, 46 and 21 are parts, and 67 is the total.
Subtraction fact 1: 67 – 21 = 46
Start with the total (67).
Take away one part (21).
You are left with the other part (46).
Subtraction fact 2: 67 – 46 = 21
Again, start with the total (67).
This time, take away the other part (46).
You are left with the first part (21).
So, we understand that –
- Addition joins parts to make the total.
- Subtraction takes the total and finds the missing part.
That’s why one addition fact gives you two subtraction facts.
More Fuel Arithmetic
Let's go back to our fuel problems, but this time, we will use subtraction!
A minibus has 18 litres of fuel left. After refuelling, the fuel meter indicates 65 litres. How much fuel has been filled in the fuel tank of the minibus?
Solution:
To find out how much fuel was filled, we need to subtract the fuel that was already there from the total fuel after refuelling.
Quantity of fuel filled = 65 litres – 18 litres
Let's do it step-by-step:
Step 1: Subtract the Ones place
We need to do 5 – 8, but 5 is smaller than 8.
So, we borrow 1 Ten from the Tens place.
6 Tens become 5 Tens, and the 5 Ones become 15 Ones.
Now, 15 – 8 = 7.
Write 7 in the Ones place.
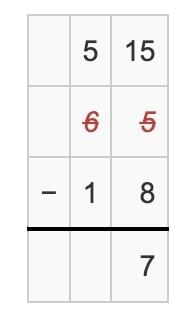
Step 2: Subtract the Tens place
Now we have 5 Tens – 1 Ten = 4 Tens.
Write 4 in the Tens place.
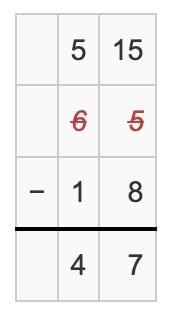
Final Answer = 47
Sums of Consecutive Numbers
What are consecutive numbers?
They are numbers that follow each other in order, one after another, without skipping any number. It's like counting!
For example:

Now, let's look at adding these consecutive numbers and see what interesting patterns we find!
1. Sum of 2 consecutive numbers
 These sums are always odd.
These sums are always odd.
(Reason: One number is even and the other is odd. Even + Odd = Odd)
2. Sum of 3 consecutive numbers
 These sums keep changing between even and odd.
These sums keep changing between even and odd.
(Reason: Adding three numbers mixes even and odd in different ways.)
3. Sum of 4 consecutive numbers

These sums are always even.
(Reason: When you add an even count of consecutive numbers, the total is always even.)
Let's Explore!
Solution:
2 consecutive → Always odd
3 consecutive → Sometimes even, sometimes odd
4 consecutive → Always even
Solution:
For 2 consecutive numbers: Difference is always 2
For 3 consecutive numbers: Difference is always 3
For 4 consecutive numbers: Difference is always 4
Quick Tip:
For an odd number of consecutive numbers, the sum is the middle number multiplied by the count of numbers. For an even number of consecutive numbers, the sum is the (first number + last number) multiplied by (count of numbers / 2).
The Longest Land Route — Adding Large Numbers
Imagine travelling really, really far! The longest road trip you can take on Earth is between a place called Talon in Russia and Sagres in Portugal. This road is super long, about 15,150 kilometres!
In India, the North–South Corridor (2019) was the longest land route.
It started from Srinagar (Jammu & Kashmir) in the north.
It ended at Kanniyakumari (Tamil Nadu) in the south.
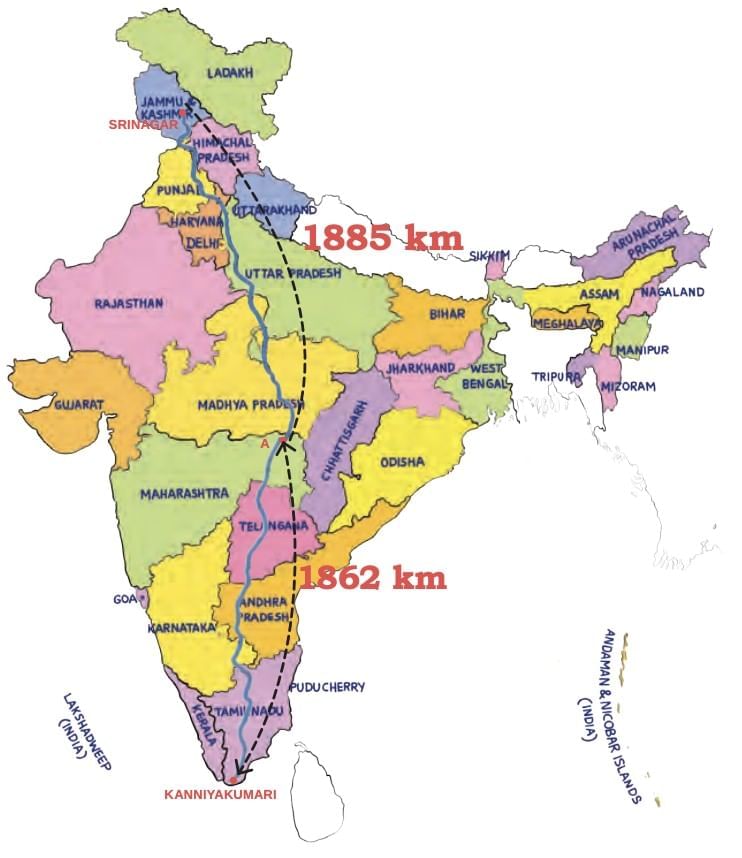
Now, let's talk about India. In 2019, we had a very long road called the North–South Corridor.
It started from Srinagar in Jammu and Kashmir and went all the way down to Kanniyakumari in Tamil Nadu. How long was it?
This corridor that was 1,855 km from Srinagar and 1,862 km from Kanniyakumari.
Let’s Find Out
The North–South Corridor connects Srinagar and Kanniyakumari. If one place is 1,855 km from Srinagar and another is 1,862 km from Kanniyakumari, what will be the total length of the corridor in 2019?
Solution:
To find the total length, we need to add the two given lengths.
Total = 1,855 km + 1,862 km

It's just like adding smaller numbers, but with more digits! We use place values like Thousands, Hundreds, Tens, and Ones.
Write the numbers in column form and start adding.
Step 1: Add the Ones place
- 5 + 2 = 7
- Put the 7 in Ones place
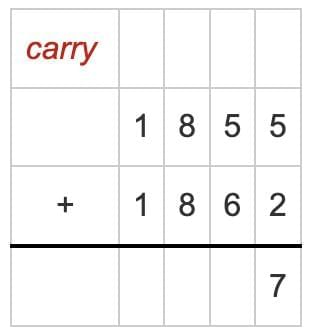
Step 3: Add the Tens place
- 5 + 6 = 11
- Put the 1 in Tens place
- Carry the 1 to Hundreds place
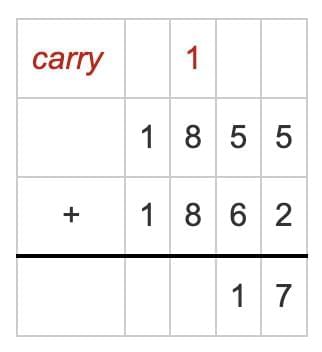
Step 4: Add the Hundreds place (with carry)
- 1 + 8 + 8 = 17
- Put the 7 in Hundreds place
- Carry the 1 to Thousands place
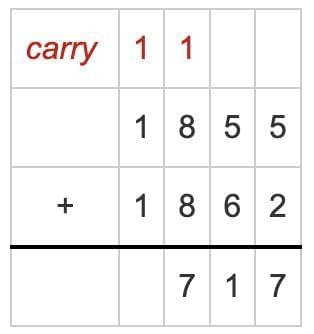
Step 5: Add the Thousands place (with carry)
- 1 + 1 + 1 = 3
- Put the 3 in Thousands place
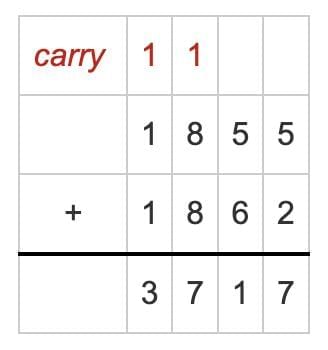
Now, let’s practise adding numbers with five digits.
Mahesh and his family decide to drive from Srinagar to Kanniyakumari. He spends ₹21,880 on fuel and toll tax, and ₹38,900 on other expenses during this journey. How much did he spend in total?
Solution:
Fuel & toll tax = ₹21,880
Other expenses = ₹38,900
Total Expenses = ₹21,880 + ₹38,900
Mahesh spent a total of ₹60,780 on his journey.
Subtracting Large Numbers
Just as we can add large numbers, we can also subtract them! Subtraction helps us in real life when we want to know how much is left, how far one value is from another, or the difference between two big numbers.
Important Places for Travel
- A bus stand or bus station is where passengers get on a bus.
- A railway station is where people get on trains.
- A port is where people get on ships.
- Your textbook talks about the ports of Mumbai and Chennai, which are very important in India. Ships travelling from Mumbai to Chennai pass by another important port called Cochin Port. You can spot these places on the map of India!
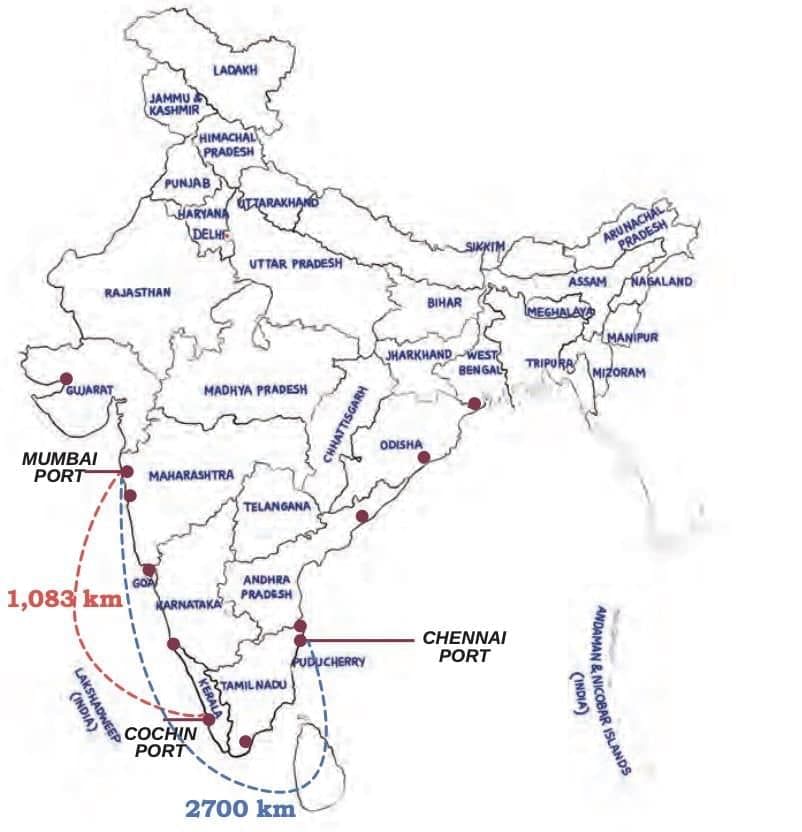
Let’s understand subtraction through a trip — it shows the distance left to cover.
The total distance of the sea route from Mumbai to Chennai is 2,700 km. A ship starting from Mumbai first reaches the Cochin port, travelling 1,083 km by sea. How much more distance does it have to travel to reach the Chennai port?
Solution:
To find the remaining distance, we need to subtract the distance already travelled from the total distance:
Remaining distance = 2,700 km – 1,083 km
Let's do it step-by-step:
Arrange all the numbers in columns based on their place value, and work through each column starting from the right.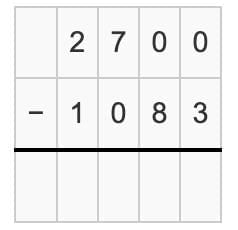
Step 1: Ones place
- 0 - 3
- Since 0 is smaller than 3, we borrow 1 from the Tens place.
- Now, 10 - 3 = 7.
- Write 7 in the Ones place.
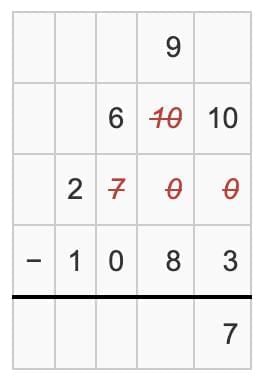
Step 2: Tens place
- 0 (after borrowing) - 8
- Since 0 is smaller than 9, we borrow 1 from the Hundreds place.
- Now, 10 - 9 = 1.
- Write 1 in the Tens place.
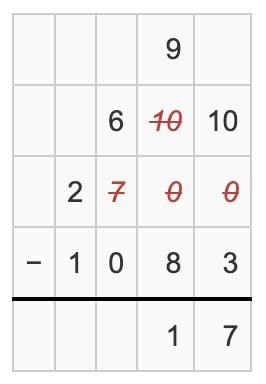
Step 3: Hundred's place
- 6 (after borrowing) - 0 = 6.
- Write 6 in the Hundreds place.
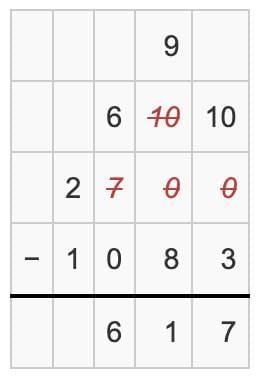
Step 3: Thousand's place
- 2 - 1 = 1.
- Write 1 in the Thousands place.
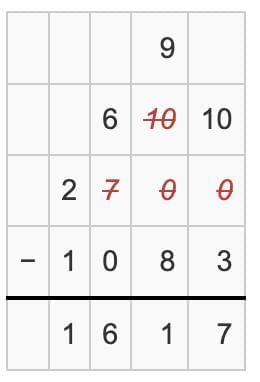
Final Answer: Remaining distance = 1617 km . The ship has to travel 1,617 km more to reach Chennai.
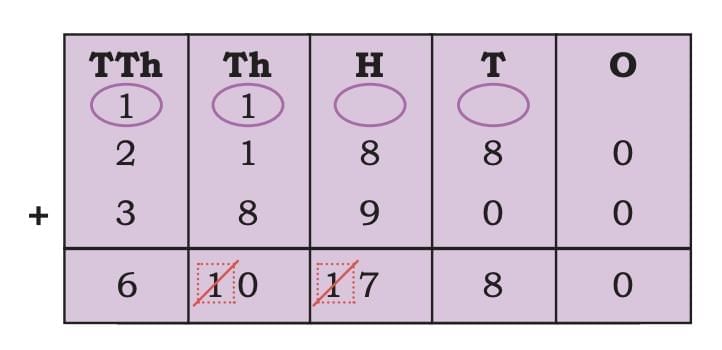
Now, let’s practise subtracting numbers with five digits.
The longest land route stretches 15,150 km from Talon (Russia) to Sagres (Portugal). In Africa, the longest highway is 10,228 km, linking Cairo (Egypt) to Cape Town (South Africa). How much longer is the land route from Talon to Sagres compared to the highway between Cairo and Cape Town?
Solution:
To find out how much longer one route is than the other, we need to find the difference between their lengths. This means we subtract the smaller length from the larger length.
Difference = 15,150 km – 10,228 km
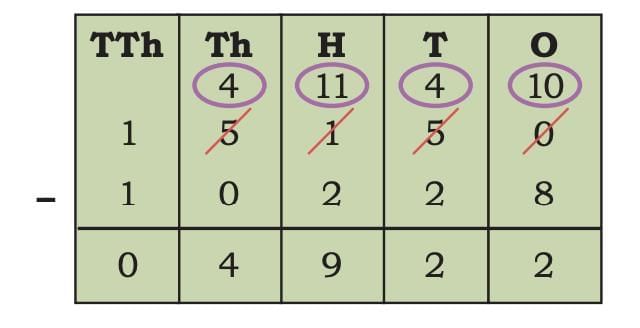
The land route connecting Talon and Sagres is 4,922 km or longer than the road connecting Cairo and Cape Town.
Mental Subtraction
Like addition, here too we can try not to write the positions of the digits and align the numbers appropriately. You can mentally keep track of the position of the digits.
For example:

Here, you mentally subtract 4 from 3 (regroup), then 5 from 0 (regroup), then 1 from 5.
Quick Sums and Differences
Let’s explore some interesting methods to solve this!
Sukanta’s friend Piku shows him an interesting way to solve the problems.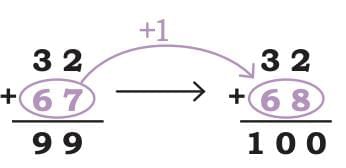
Let's help him fill in the blanks!
32 _______ = 100
Sukanta likes the numbers 10, 100, 1,000, and 10,000. He wants to figure out what number he should add to a given number such that the sum is 100 or 1,000.
- To find the missing number, you can think: "How much more do I need to add to 32 to reach 100?" This is a subtraction problem: 100 - 32 = 68.
- Piku's Method
Sukanta’s friend Piku shows him an interesting way to solve these problems:
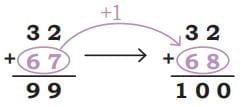
Then, add 1 to the sum:
This method is a bit tricky. Let's understand it better. Piku is trying to make the number easier to work with by getting it close to 100. If you add 67 to 32, you get 99. Then, adding 1 more makes it 100. So the missing number = 68.
Trying Piku's Method
Do you think this method will always work? Let's try this method for the number 59:
- 59 _______ = 100
- Using Piku's method:
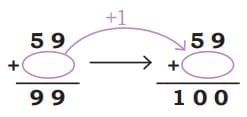
Then, add 1 to the sum:
So, the missing number is = 100
Piku's Method Explained
This method works by finding the difference to the next multiple of 10, then to 100. For example, for 32 to reach 100: 32 + 8 = 40, then 40 + 60 = 100. So 8 +60 = 68.
Piku's method is a variation of this, where you try to reach 99 first, and then add 1.
Units Digit is 0
Will this method work if the units digit is 0? What do you think?
Let's try with numbers ending in 0:
- (a) 180 ________ = 1,000 If we use Piku's method, we would try to reach 999. But 180 already ends in 0. It's easier to just subtract: 1,000 - 180 = 820. So, 180 + 820 = 1,000.
- (b) 760 ________ = 1,0001,000 - 760 = 240. So, 760 + 240 = 1,000.
- (c) 400 ________ = 1,0001,000 - 400 = 600. So, 400 + 600 = 1,000.
Other Methods to Find Missing Numbers
- The simplest method is always to subtract the given number from the target sum. For example, to find the missing number in A ? = B, you just calculate B - A = ?.
Namita's Challenge
Namita likes the number 9. She wants to subtract 9 or 99 from any number. Let's find a way to quickly subtract 9 or 99 from any number.
Quick Tricks
- To subtract 9: Subtract 10, then add 1. Example: 67 - 9 Think: 67 - 10 = 57. Then, 57 + 1 = 58.
- To subtract 99: Subtract 100, then add 1. Example: 187 - 99 Think: 187 - 100 = 87. Then, 87 + 1 = 88.
- Let's try the examples
- (a) 67 – 9 = ________ 67 - 10 = 57. 57 + 1 = 58.
- (b) 83 – 9 = ________ 83 - 10 = 73. 73 + 1 = 74.
- (c) 144 – 9 = ________ 144 - 10 = 134. 134 + 1 = 135.
- (d) 187 – 99 = ________ 187 - 100 = 87. 87 + 1 = 88.
- (e) 247 – 99 = ________ 247 - 100 = 147. 147 + 1 = 148.
- (f) 763 – 99 = ________ 763 - 100 = 663. 663 + 1 = 664.
- Now, use the above solutions to find answers to the following problems. Do not calculate again.
- Namita wonders if she can get 9 or 99 as the answer to any subtraction problem. Find a way to get the desired answer.
- (a) 32 – ________ = 9 We know that 32 - 23 = 9. So the missing number is 23. (Think: 32 - 9 = 23)
- (b) 56 – ________ = 9 We know that 56 - 47 = 9. So the missing number is 47. (Think: 56 - 9 = 47)
- (c) 877 – ________ = 99 We know that 877 - 778 = 99. So the missing number is 778. (Think: 877 - 99 = 778)
- (d) 666 – ________ = 99 We know that 666 - 567 = 99. So the missing number is 567. (Think: 666 - 99 = 567)
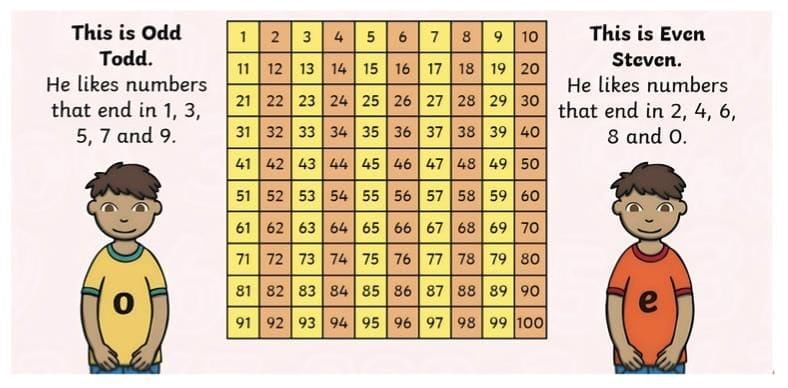
Even and Odd Numbers
Even Numbers:
- These are numbers that can be divided into two equal groups without anything left over.
- They always end in 0, 2, 4, 6, or 8.
- Examples: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
Odd Numbers:
- These are numbers that cannot be divided into two equal groups. When you try to divide them by 2, there's always 1 left over.
- They always end in 1, 3, 5, 7, or 9.
- Examples: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19...
Arrangements of Odd and Even in Pairs.
A useful way to understand even and odd numbers is through paired arrangements. This will help us visualise whether a number is even or odd.
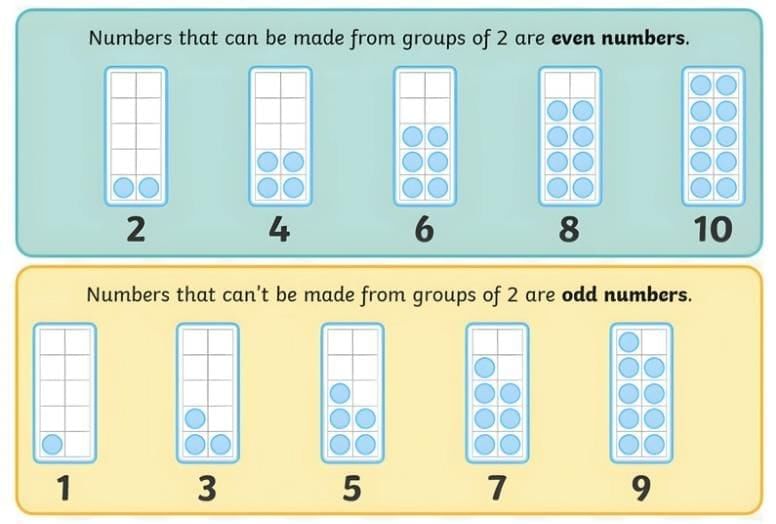 Let's examine this through the following paired arrangements.
Let's examine this through the following paired arrangements.
- Paired arrangement for 18: If you arrange 18 items in pairs, you will have 9 pairs, and nothing will be left over.
This shows 18 is an even number. - Paired arrangement for 23: If you arrange 23 items in pairs, you will have 11 pairs, and 1 item will be left over.
This shows 23 is an odd number.
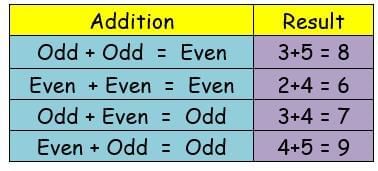
Understanding Sums of Even and Odd Numbers
Now that we’ve seen how to pair numbers, let’s examine what happens when we add even and odd numbers. This section will help you understand the sum of even and odd numbers and recognise patterns in their behaviour. Do the sums behave the same for all pairs?
Let’s explore this!
If you add 2 to 18, you get 20. When you arrange 20 items in pairs, you will still have no items left over. So, adding 2 to an even number keeps it an even number. The arrangement will still be perfectly paired.
If you add 2 to 23, you get 25. When you arrange 25 items in pairs, you will still have 1 item left over. So, adding 2 to an odd number keeps it an odd number. The arrangement will still have one item left over.
Based on this, it is clear that
Even + Even = Even
Odd + Odd = Even
Even + Odd = Odd
|
35 videos|318 docs|7 tests
|
FAQs on We the Travellers—II Chapter Notes - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What is the main relationship between addition and subtraction? |  |
| 2. How can we quickly add large numbers? |  |
| 3. What are the characteristics of even and odd numbers? |  |
| 4. How do you find the sum of consecutive numbers? |  |
| 5. What strategies can be used for quick subtraction of large numbers? |  |


















