We the Travellers — 1 Chapter Notes | Mathematics for Class 5 PDF Download
Introduction
People have always travelled — first on foot and animals, later using boats, carts, and trains, and today with cars, planes, and even spacecraft. With so many vehicles and such long distances, we often use large numbers. 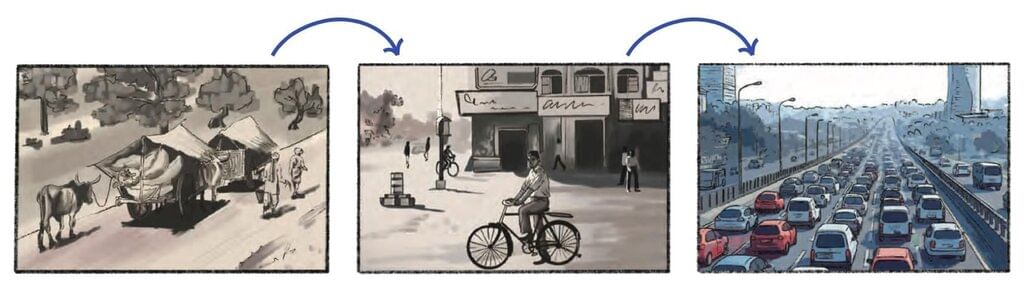 Transition of means of transportation over the years
Transition of means of transportation over the years
For example, when we say there are more than 50,000 cars in a city or a train travels 1,200 km in a day, we are using large numbers. In this chapter, we will learn to read, write, and understand such large numbers using place value.
Reading and Writing Large Numbers
Let us start with 1,000.
What numbers do we get when we keep adding a thousand?
 If we keep adding 1,000, we get these numbers
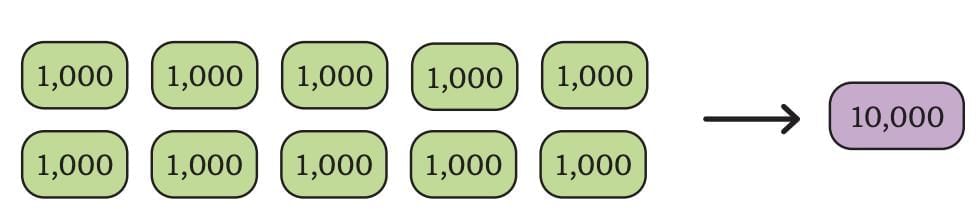
If we keep adding 1,000, we get these numbers What happens when we add 1,000 to 9,000?
What happens when we add 1,000 to 9,000? We get Ten Thousand, which is written as 10,000. To understand big numbers, we use something called a Place Value Chart.
What is a Place Value Chart?
- A Place Value Chart is a table that helps us know the value of each digit in a number by showing its place.
- The value of a digit depends on whether it is in the Ones place, Tens place, Hundreds place, Thousands place, or beyond.
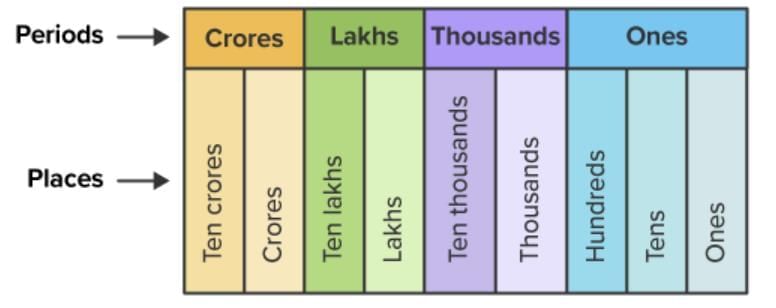
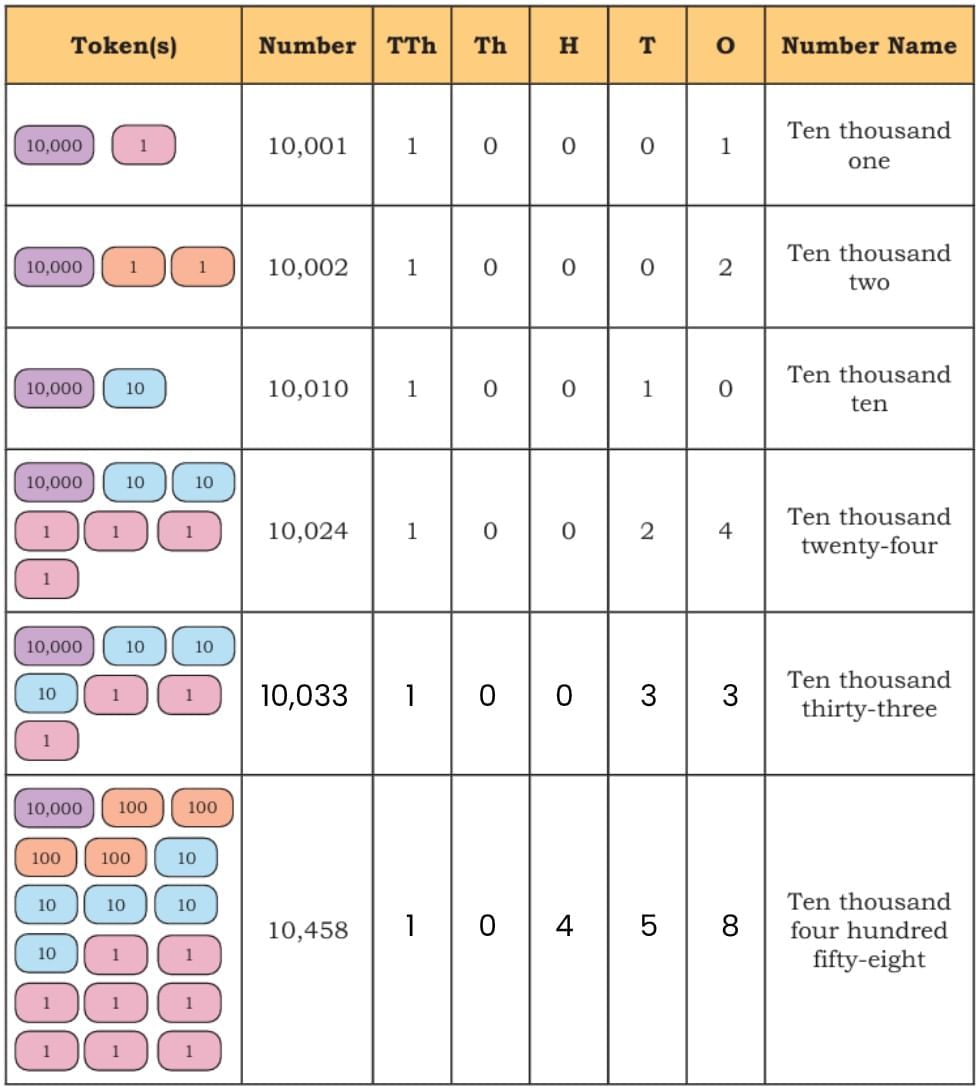
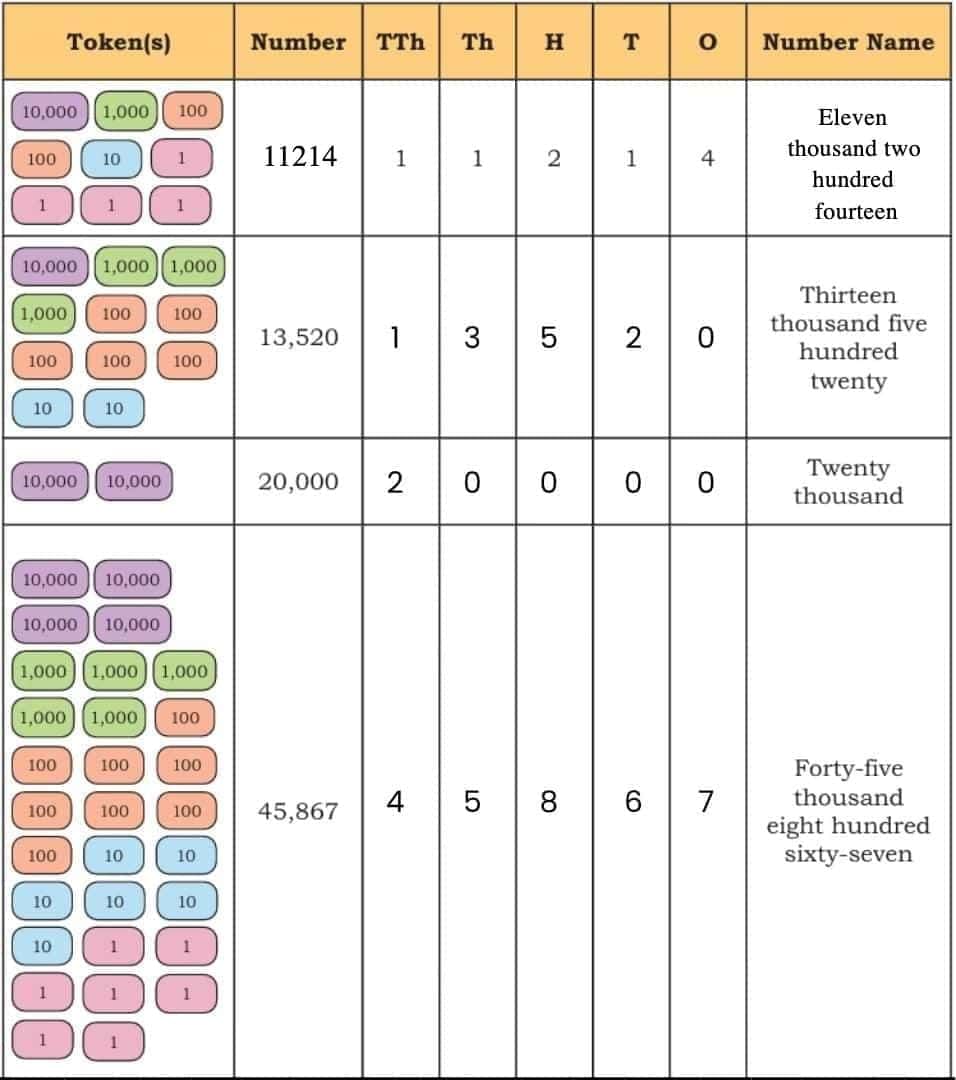
Look at the table below and notice the pattern of writing numbers: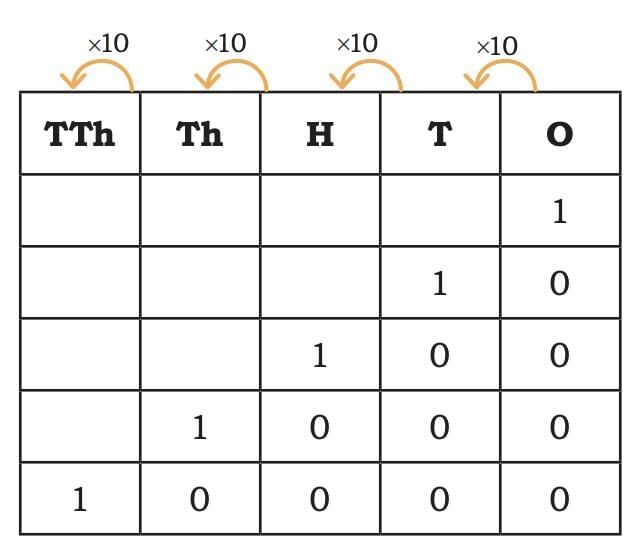 Here, notice the first column - TTh, which stands for Ten Thousand.
Here, notice the first column - TTh, which stands for Ten Thousand.
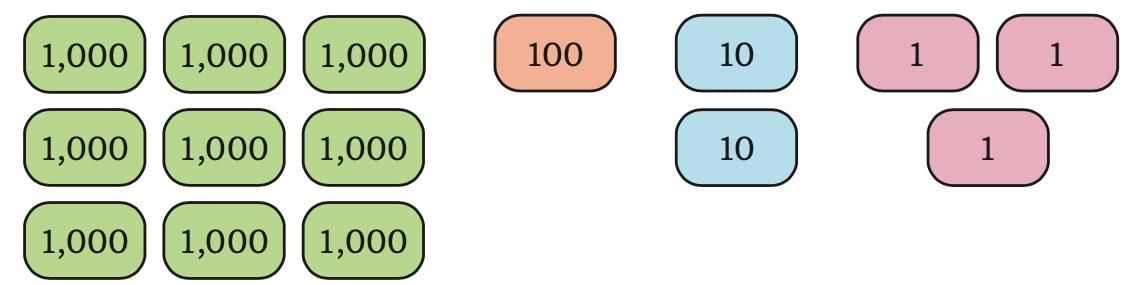
 • 10 Ones make 1 Ten (10)
• 10 Ones make 1 Ten (10) 

 Now that we know the place value system (Ones, Tens, Hundreds, Thousands, Ten Thousands), we can see that numbers become longer and harder to read. To make large numbers easier to read and write, we use commas to separate them according to their place values.
Now that we know the place value system (Ones, Tens, Hundreds, Thousands, Ten Thousands), we can see that numbers become longer and harder to read. To make large numbers easier to read and write, we use commas to separate them according to their place values.
Commas in Large Numbers
Commas help us read large numbers easily.
In the Indian system:
- Starting from the right side, put the first comma after 3 digits (Ones).
- Then put commas after every 2 digits.
For example:
- 1. Start with the number: 8045
- Without commas, it looks like just four digits in a row.
- 2. Place commas from the right side:
- First comma comes after 3 digits → 8,045
- 3. Now read using place values:
- 8 = Thousands
- 0 = Hundreds
- 4 = Tens
- 5 = Ones
So, 8,045 = Eight thousand forty-five
Now that we can read numbers using commas, let’s also break them into parts to see the value of each digit. This is called the expanded form.
Expanded Form of Large Numbers
The expanded form of a number shows the value of each digit according to its place value.
It “expands” the number into a sum of its digits multiplied by their place values.
For example,
- 1,380 = 1 Thousand + 3 Hundreds + 8 Tens + 0 Ones.
 1380 will be read as One Thousand Three Hundred Eighty
1380 will be read as One Thousand Three Hundred Eighty - 9,123 = 9 Thousands + 1 Hundred + 2 Tens + 3 Ones.
 9123 will be read as Nine Thousand One Hundred Twenty Three
9123 will be read as Nine Thousand One Hundred Twenty Three
Let us see how we write numbers beyond 10,000 and how we name them. We write them in the same way as numbers below 9,999.
Numbers are not only written in expanded form, but they can also follow certain rules. We kept adding 1,000 and saw the numbers 10,000, 11,000, 12,000 … Did you notice something? The numbers are following a rule. Such rules are called patterns. Let’s explore more number patterns.
Patterns in Numbers
A number pattern is a sequence of numbers that follow a certain rule. The rule may be adding, subtracting, multiplying, or dividing by the same number again and again. Patterns help us find the next number without counting each time.
Let us understand by looking at the following example:

Look at the numbers: 456 → 567 → 678
What is happening?
- 456 + 111 = 567
- 567 + 111 = 678
So, we keep adding 111 each time.
Continue the Pattern:
- 678 + 111 = 789
- 789 + 111 = 900
- 900 + 111 = 1,011
- 1011 + 111 = 1122
Final Pattern:
Ascending and Descending Order
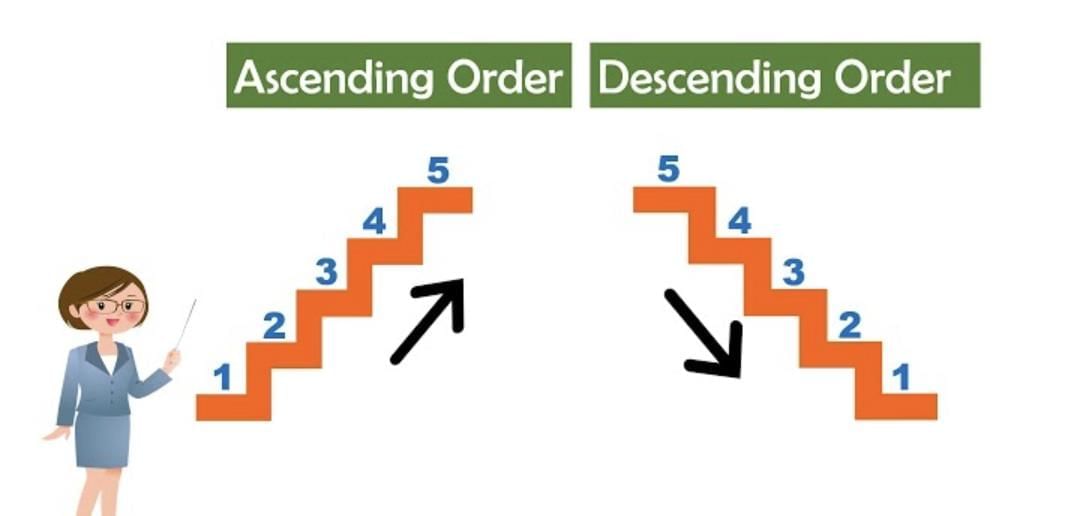
1. What is Ascending Order?
Ascending order means arranging numbers from the smallest to the largest.
Start with the smallest number
End with the largest number
Example 1: Arrange 45, 12, 78, 33 in ascending order.
Step 1: Identify the smallest number → 12
Step 2: Next smallest → 33
Step 3: Next → 45
Step 4: Largest → 78
Answer (Ascending Order): 12, 33, 45, 78
2. What is Descending Order?
Descending order means arranging numbers from the largest to the smallest.
Start with the largest number
End with the smallest number
Example 2: Arrange 45, 12, 78, 33 in descending order.
Step 1: Identify the largest number → 78
Step 2: Next largest → 45
Step 3: Next → 33
Step 4: Smallest → 12
Answer (Descending Order): 78, 45, 33, 12
Quick Tip:
Ascending = “Add up” → Small to Large
Descending = “Drop down” → Large to Small
Always check the highest place value first.
Nearest Tens (10s), Hundreds (100s), and Thousands (1,000s)
Patterns show us how numbers grow. But numbers can also take shortcuts by rounding off to the nearest 10, 100, or 1000. Let’s follow our rabbit friend to see how.Part 1: Nearest Tens of 2,346
Situation:
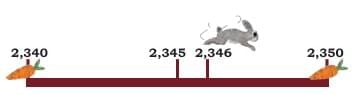
- The rabbit is standing at 2,346.
- The food is kept at the neighbouring tens — these are the numbers that are 10 apart from 2,346.
- The two closest tens are:
- 2,340 (just before 2,346)
- 2,350 (just after 2,346)
What to do: We check which one is closer to 2,346.
- From 2,346 to 2,340: 6 jumps back
- From 2,346 to 2,350: 4 jumps forward
Answer:
- 2,350 is the nearest ten to 2,346
- It will need 4 jumps to reach 2,350
Part 2: Nearest Hundreds of 2,346
Situation:
- The rabbit is still at 2,346
- The food is now kept at neighbouring hundreds
- The two closest hundreds are:
- 2,300
- 2,400
What to do: We check which one is closer to 2,346.
- From 2,346 to 2,300: 46 jumps back
- From 2,346 to 2,400: 54 jumps forward
Answer:
- 2,300 is the nearest hundred to 2,346
- It will need 46 jumps to reach 2,300
Part 3: Nearest Thousands of 2,346
Situation:
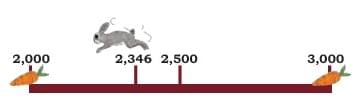
- The rabbit is still at 2,346
- The food is now kept at neighbouring thousands
- The two closest thousands are:
- 2,000
- 3,000
What to do: We check which one is closer to 2,346.
- From 2,346 to 2,000: 346 jumps back
- From 2,346 to 3,000: 654 jumps forward
Answer:
- 2,000 is the nearest thousand to 2,346
- It will need 346 jumps to reach 2,000
Travelling, Now and Then
 Means of Transport
Means of Transport- We learnt that people in the past travelled on foot, on animals, and used boats and sailing ships.
- The animals that have been used for travelling include bullocks, horses, donkeys, mules, and elephants.
- In hilly and snow-covered regions, yaks, dogs, and reindeers have been used, while camels have been used in deserts.
- Now, people use bicycles, motorbikes, cars, buses, trains, ships, and aeroplanes to travel from one place to another.
- Submarines are used to go deep under water.
- Humans are also using spacecraft to travel to outer space.
In an hour a person can generally travel:
- On foot: 3 – 5 km
- On horseback: 10 – 15 km
- By cycle: 12 – 20 km
- By motorbike: 40 – 60 km
- By train: 40 – 160 km
- By ship: 25 – 45 km
- By aircraft: 750 – 920 km
- By spacecraft: minimum 28,000 km
Finding Large Numbers Around Us
We have seen that the distance covered by different means of transport in one hour can range from a 1-digit number to a 5-digit number.
But numbers of this size are not found only in distances. Can we find other examples of such large numbers in our everyday life? Let’s look at one.
Consider a book that has around 200 pages, and each page has about 50 words.
The total number of words in the book will be approximately:
200 × 50 = 10,000 words
This shows how large numbers appear even in things we use every day.
We usually measure long distances on sea and in the air using nautical miles, but for now, we can use the simple conversion 1 km = 1,000 m. By now, you are familiar with different units of length. We will study the kilometre and its uses in detail in a later chapter.
Pastime Mathematics
Sanju and Mira are traveling on a train. To pass time, they challenge each other with games and puzzles.

The River Crossing Puzzle
A boatman wants to cross a river in a boat. He has to take a lion, a sheep, and a bundle of grass with him. He can take one of them at a time. If the sheep and grass are left on the shore, the sheep will eat the grass. And, if the sheep and lion are left on the shore, the lion will eat the sheep. How can the boatman take the lion, sheep, and grass across the river? Help him so that he can ferry the lion, sheep, and grass across the river safely, and in the minimum number of trips.
A boatman wants to cross a river with:
A lion
A sheep
A bundle of grass
Rules
The boat is very small and can carry only one item at a time with the boatman.
If left alone, the sheep will eat the grass.
If left alone, the lion will eat the sheep.
Goal: Help the boatman take all three to the other side safely in the least number of trips.

Solution
First Trip: Take the sheep across.
Other side: Sheep
Starting side: Lion, Grass
Second Trip: Return alone, take the lion across, and bring the sheep back.
Other side: Lion
Starting side: Grass
Boat: Sheep
Third Trip: Take the grass across.
Other side: Lion, Grass
Starting side: Sheep
Final Result:
All three — lion, sheep, and grass — reach safely.
Total Trips: 7 (4 trips with passengers + 3 trips back alone or with the sheep)
Pile of Pebbles Game
Sanju introduces a game called pile ofpebbles to Mira. There are two piles of pebbles. Each pile contains 7 pebbles. Each player can pick as many pebbles as they want from either of the piles. The player who picks the last pebble wins. Try this game with your friends. Now, how do you play so that you win? To find a winning strategy, try playing with 1 pebble in each pile, two in each, three in each, and so on.

How to Play the Game
There are two piles of pebbles.
Each pile has 7 pebbles at the beginning.
Rules of the Game:
Two players take turns.
On your turn, you can pick any number of pebbles (1 or more) but only from one pile.
You cannot pick pebbles from both piles in the same turn.
The player who picks the last pebble — that is, there are no pebbles left in both piles after their move — wins the game.
What’s the Challenge?
Mira asks: "How can I make sure I win this game?"
Sanju tells her: "Try playing the game with smaller numbers of pebbles, like 1 in each pile, then 2 in each pile, and so on. Look for a pattern to find a winning strategy."
Let’s Try Small Examples First
Example 1: 1 pebble in each pile (1, 1)
Player 1 takes all the pebbles from one pile.
Player 2 takes the last pebble from the other pile — and wins.
So, if it starts at (1, 1), the second player wins.
Example 2: 2 pebbles in each pile (2, 2)
Player 1 takes 2 from one pile → (0, 2)
Player 2 takes 2 from the other pile → (0, 0) → Player 2 wins again
Again, (2, 2) is a losing position for the first player.
Example 3: 3 in each pile (3, 3)
Same pattern continues. If both piles are equal, the second player can always copy what the first player does, and win.
What Pattern Do We See?
If the two piles have the same number of pebbles, then the second player can always win by copying the first player's moves.
But if the two piles have different numbers, then the first player can win if they know what to do.
Winning Strategy
To win the game:
Try to leave the piles in a position where both piles have the same number of pebbles for your opponent.
Then, whatever number they take from one pile, you take the same number from the other pile.
Keep copying their move until you get the last pebble.
In Our Case (7, 7)
The game starts with 7 pebbles in each pile.
If you go second, you can win by copying your opponent’s moves.
If you go first, you should try to make the piles equal after your move, so the second player cannot copy you and win.
The Number Puzzle
Now it’s Mira’s turn to give a puzzle to Sanju.
She gives him a fun number puzzle that looks simple at first, but has an amazing surprise in the end.
How to Play the Puzzle
Let’s understand the steps clearly:
Step 1:
Pick any two different digits.
For example: 3 and 7
Step 2:
Make two 2-digit numbers using those digits.
You can make:
37 (3 first, 7 second)
73 (7 first, 3 second)
Step 3:
Subtract the smaller number from the bigger number.
Here:
73 – 37 = 36
Step 4:
Now use the two digits of the result (which is 3 and 6)
and repeat Steps 2 and 3.
Let’s do it:
36 and 63
63 – 36 = 27
Use 2 and 7 now:
27 and 72
72 – 27 = 45
Use 4 and 5:
45 and 54
54 – 45 = 9
Now we got a single-digit number — 9.
Mira's Surprise
Mira says:
"No matter which two digits you start with, you will always end up with 9."
The whole process will look as shown below.

This makes the puzzle magical and fun. But how did she know that?
Let’s Explore the Pattern
Let’s take a closer look at the examples:
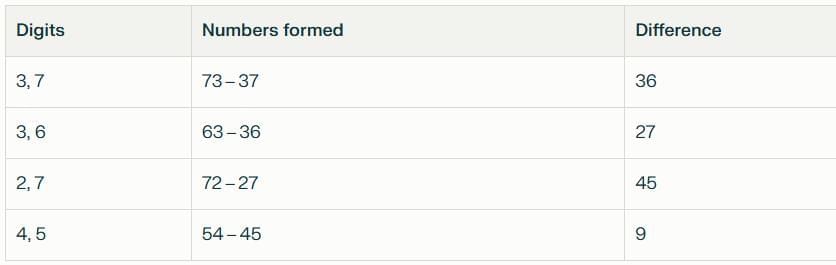
Look at the differences:
36 → 27 → 45 → 9
Each time, we use the digits from the result and continue.
Eventually, we reach 9, a single-digit number.
Try with Other Digits
Let’s try starting with 1 and 9:
91 – 19 = 72
Use 7 and 2 → 72 – 27 = 45
Use 5 and 4 → 54 – 45 = 9
Again, we get 9.
What’s the Trick or Pattern?
Look at this:
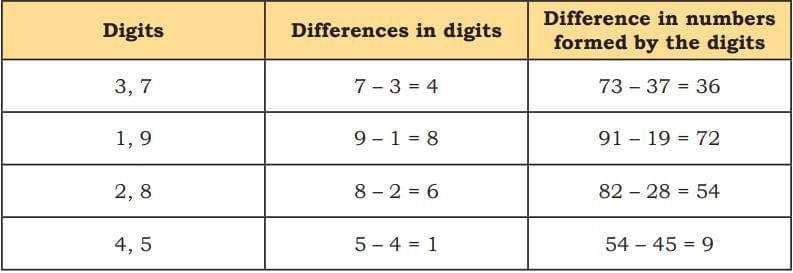
Now look at the relationship:
36 ÷ 4 = 9
72 ÷ 8 = 9
54 ÷ 6 = 9
9 ÷ 1 = 9
So, the difference between the two numbers is always a multiple of 9.
That’s how Mira knew that the process will always end at 9.
Try This Yourself
Try different starting digits and make your own table:
Choose digits so that the difference between the numbers is 2, 3, 5, or 7.
See what pairs of digits give you 9 in just one or two steps.
See which pairs take the longest time (most steps) to reach 9.
King's Horses
There was once a king who loved horses a lot. He had 20 beautiful horses. The king kept his horses in a big building called a stable. There, a man called a caretaker took care of the horses for the king.
One day, a thief sneaked in at night and stole one horse! Now there were only 19 horses left. The caretaker was scared that the king would be angry if he found out a horse was missing.
So, the clever caretaker tried to trick the king! He arranged the horses in a way so that when the king looked, he saw 5 horses on each side of the stables, and there are 4 sides. The king counted: 5 on this side, 5 on that side, 5 on another, and 5 on the last, which makes 20 horses. The king thought all the horses were there and went away happy.
But there really weren’t 20 horses left!
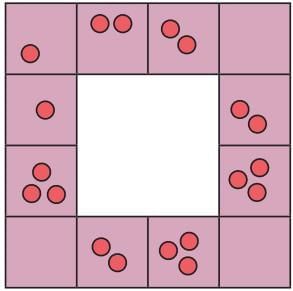
If you count the horses one by one, you’ll see there are only 19 horses. So, what was the caretaker’s trick?
Here’s the trick:
The caretaker put some horses at the corners of the square. These corner horses are counted on both sides — for both sides they are on! For example, if there’s a horse in the left corner, you might count it for the left and the top sides.
So, the king was counting the same horse twice for two sides!
The next night, the thief came again and took one more horse. Now only 18 horses were left. The caretaker moved the horses again, so the king saw 5 horses on each side the next day.
|
95 videos|462 docs|47 tests
|
FAQs on We the Travellers — 1 Chapter Notes - Mathematics for Class 5
| 1. What are nearest tens, hundreds, and thousands, and how can we find them? |  |
| 2. How can we apply the concept of large numbers in our daily lives? |  |
| 3. What is the importance of learning mathematics in the context of traveling? |  |
| 4. Can you give an example of how to find large numbers around us? |  |
| 5. What are some fun activities to practice mathematics related to travel? |  |






















