Class 8 Exam > Class 8 Notes > Mathematics Class 8 ICSE > Chapter notes: Area of a Trapezium and a Polygon
Chapter notes: Area of a Trapezium and a Polygon | Mathematics Class 8 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| REVIEW |

|
| PERIMETER AND AREA OF TRIANGLES |

|
| PERIMETER AND AREA OF RECTANGLES |

|
| PERIMETER AND AREA OF SQUARES |

|
| TRAPEZIUM |

|
| PARALLELOGRAM |

|
| RHOMBUS |

|
| CIRCLE |

|
Introduction
The chapter "Area of Trapezium and a Polygon" introduces students to the concepts of measuring the perimeter and area of various shapes like triangles, rectangles, squares, trapeziums, parallelograms, rhombuses, and circles. It explains how to calculate the boundary length (perimeter) and the surface area enclosed by these shapes using specific formulas. The chapter also covers unit conversions for length and area measurements and provides methods to find dimensions or areas of shapes based on given conditions. Through step-by-step explanations, students learn to apply these formulas to solve real-world problems involving geometric figures.
REVIEW
- Perimeter: The total length of the boundary of a shape.
- Area: The amount of surface enclosed within the boundary of a shape.
- Units for Perimeter: Measured in meters (m), centimetres (cm), decimeters (dm), millimetres (mm), etc.
- Unit Conversions for Length:
- 1 m = 100 cm, 1 cm = 0.01 m
- 1 m = 10 dm, 1 dm = 0.1 m
- 1 dm = 10 cm, 1 cm = 0.1 dm
- 1 m = 1000 mm, 1 mm = 0.001 m
- Units for Area: Measured in square meters (m²), square centimetres (cm²), square millimetres (mm²), etc.
- Unit Conversions for Area:
- 1 m² = 10,000 cm², 1 cm² = 0.0001 m²
- 1 m² = 100 dm², 1 dm² = 0.01 m²
- 1 dm² = 100 cm², 1 cm² = 0.01 dm²
Example: If a shape has a boundary length of 500 cm, convert this perimeter to meters.
Solution:
Solution:
- Since 1 m = 100 cm, divide the perimeter by 100.
- Perimeter = 500 cm ÷ 100 = 5 m.
PERIMETER AND AREA OF TRIANGLES
- Perimeter: Sum of all three sides of a triangle (a + b + c).
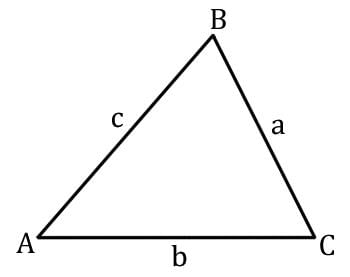
- Area Using Sides (Heron’s Formula):
- Step 1: Calculate semi-perimeter, s = (a + b + c) / 2.
- Step 2: Area = √[s(s - a)(s - b)(s - c)].
- Area Using Base and Height:
- Area = (1/2) × base × height.
Example : The base of an isosceles triangle is 12 cm, and its perimeter is 32 cm. Find its area.
Solution:
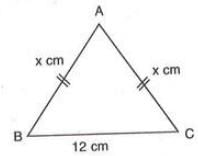
Solution:

- Let each equal side be x cm. Perimeter = x + x + 12 = 32 → 2x = 20 → x = 10 cm.
- Sides are 10 cm, 10 cm, 12 cm. Semi-perimeter, s = (10 + 10 + 12) / 2 = 16 cm.
- Area = √[16(16 - 10)(16 - 10)(16 - 12)] = √[16 × 6 × 6 × 4] = √2304 = 48 cm².
Alternative Method: Draw perpendicular AD from vertex A to base BC, bisecting BC.
- BD = CD = 12 / 2 = 6 cm. In right triangle ABD, AD² = AB² - BD² = 10² - 6² = 64 → AD = 8 cm.
- Area = (1/2) × base × height = (1/2) × 12 × 8 = 48 cm².
PERIMETER AND AREA OF RECTANGLES
- Perimeter: 2 × (length + breadth) = 2(l + b).
- Area: length × breadth = l × b.
- Diagonal: √(length² + breadth²) = √(l² + b²) [Using Pythagoras' Theorem].
Example : The perimeter of a rectangle is 28 cm, and its length is 8 cm. Find its breadth, area, and diagonal.
Solution:
Solution:
- Perimeter = 2(l + b) → 28 = 2(8 + b) → 8 + b = 14 → b = 6 cm.
- Area = l × b = 8 × 6 = 48 cm².
- Diagonal = √(l² + b²) = √(8² + 6²) = √(64 + 36) = √100 = 10 cm.
PERIMETER AND AREA OF SQUARES
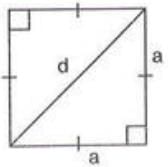
- Perimeter: 4 × side = 4a.
- Area: side × side = a².
- Diagonal: √(side² + side²) = √(2a²) = a√2.
Example: Find the perimeter and area of a square with side 5 cm.
Solution:
Solution:
- Perimeter = 4 × side = 4 × 5 = 20 cm.
- Area = side² = 5² = 25 cm².
TRAPEZIUM
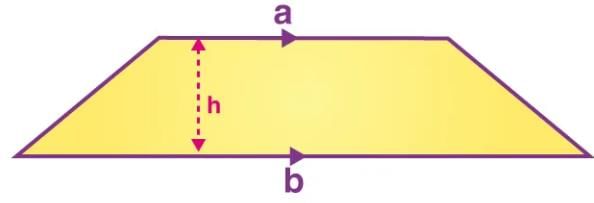
- Area: (1/2) × (sum of parallel sides) × height = (1/2) × (a + b) × h.
- Height: The perpendicular distance between the parallel sides.
Example : The parallel sides of a trapezium are in the ratio 3:5, the distance between them is 10 cm, and the area is 120 cm². Find the lengths of the parallel sides.
Solution:
Solution:
- Let parallel sides be 3x cm and 5x cm.
- Area = (1/2) × (3x + 5x) × 10 = 120 → 8x × 5 = 120 → 8x = 24 → x = 3.
- Parallel sides = 3 × 3 = 9 cm and 5 × 3 = 15 cm.
PARALLELOGRAM
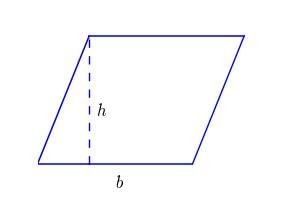
- Area: Base × corresponding height.
- Diagonals: Each diagonal divides the parallelogram into two equal triangles.
Example : A parallelogram has sides 12 cm and 8 cm. The distance between the 12 cm sides is 5 cm. Find the distance between the 8 cm sides.
Solution:
Solution:
- Area with base 12 cm = 12 × 5 = 60 cm².
- With base 8 cm, area = 8 × h = 60 → h = 60 / 8 = 7.5 cm.
RHOMBUS
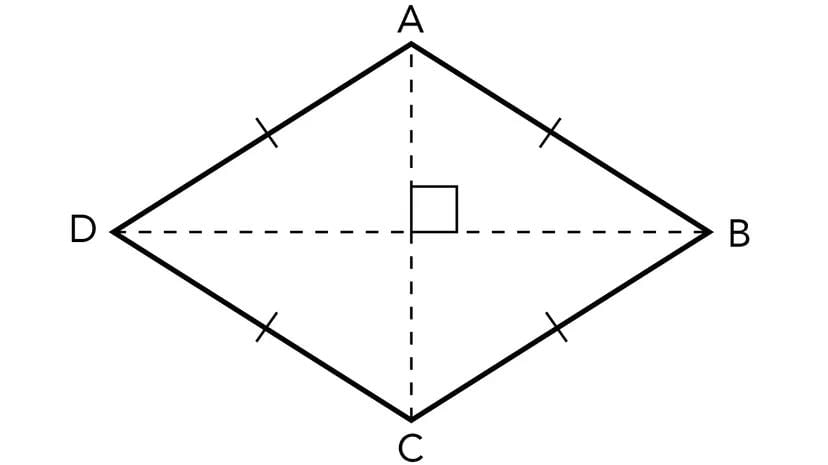
- Definition: A parallelogram with all sides equal.
- Perimeter: 4 × side = 4a.
- Area: (1/2) × product of diagonals = (1/2) × d1 × d2.
- Diagonals: Bisect each other at 90° and divide the rhombus into four equal triangles.
- Area Using Base and Height: Base × height (as it is a parallelogram).
Example : The diagonals of a rhombus are 16 cm and 12 cm. Find its area, side length, and perimeter.
Solution:
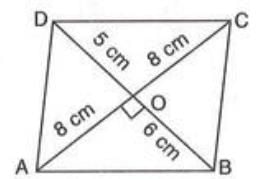
Solution:

- Area = (1/2) × 16 × 12 = 96 cm².
- Half diagonals: OA = 16 / 2 = 8 cm, OB = 12 / 2 = 6 cm.
- Side AB = √(OA² + OB²) = √(8² + 6²) = √(64 + 36) = 10 cm.
- Perimeter = 4 × 10 = 40 cm.
CIRCLE
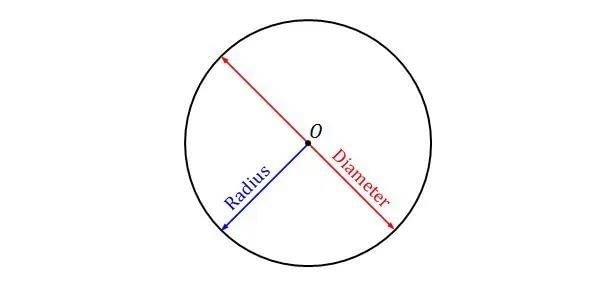
- Definition: A closed curve where all points are equidistant from a fixed center point.
- Radius: Distance from the center to any point on the circumference.
- Diameter: A line through the center joining two points on the circumference, d = 2r.
- Circumference: The perimeter of the circle = 2πr, where π = 22/7.
- Area: πr².
Example : Find the radius and area of a circle with a circumference of 132 cm.
Solution:
Solution:
- Circumference = 2πr = 132 → 2 × (22/7) × r = 132 → r = (132 × 7) / (2 × 22) = 21 cm.
- Area = πr² = (22/7) × 21² = 1386 cm².
The document Chapter notes: Area of a Trapezium and a Polygon | Mathematics Class 8 ICSE is a part of the Class 8 Course Mathematics Class 8 ICSE.
All you need of Class 8 at this link: Class 8
|
23 videos|98 docs|14 tests
|
FAQs on Chapter notes: Area of a Trapezium and a Polygon - Mathematics Class 8 ICSE
| 1. What is the formula to calculate the perimeter of a triangle? |  |
Ans. The perimeter of a triangle is calculated by adding the lengths of all three sides. The formula is P = a + b + c, where P is the perimeter and a, b, and c are the lengths of the sides.
| 2. How do you calculate the area of a rectangle? |  |
Ans. The area of a rectangle is calculated using the formula A = length × width. Here, A represents the area, while the length and width are the dimensions of the rectangle.
| 3. What is the difference between the perimeter and area of a square? |  |
Ans. The perimeter of a square is the total length around the square, calculated using the formula P = 4 × side length. The area, on the other hand, measures the space inside the square and is calculated as A = side length × side length or A = side length².
| 4. How do you find the area of a trapezium? |  |
Ans. The area of a trapezium (or trapezoid) can be calculated using the formula A = 1/2 × (base1 + base2) × height, where base1 and base2 are the lengths of the two parallel sides and height is the perpendicular distance between them.
| 5. What is the formula for the area of a circle? |  |
Ans. The area of a circle is calculated using the formula A = π × radius², where A is the area and the radius is the distance from the center of the circle to any point on its circumference.
Related Searches















