Class 8 Exam > Class 8 Notes > Mathematics Class 8 ICSE > Chapter notes: Exponents (Powers)
Chapter notes: Exponents (Powers) | Mathematics Class 8 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Exponent |

|
| Laws of Exponents (For Integral Powers) |

|
| Negative Integral Exponent |

|
| More about exponents |

|
Introduction
Exponents, also known as powers, are a way to express repeated multiplication of a number by itself. This chapter introduces the concept of exponents, their rules, and how to handle them with integers and rational numbers, including negative and zero exponents. It covers the laws of exponents and their applications in simplifying expressions, along with the behaviour of negative bases raised to even or odd powers.
Exponent
- An exponent represents how many times a number, called the base, is multiplied by itself.
- For a real number x and an integer n, xn means x multiplied by itself n times.
- xn is called an exponential expression, where x is the base and n is the exponent (or index or power).
- It is read as "x raised to the power n."
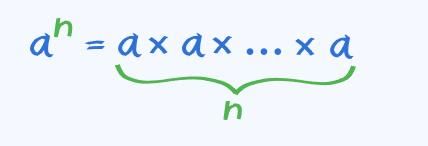
Laws of Exponents (For Integral Powers)
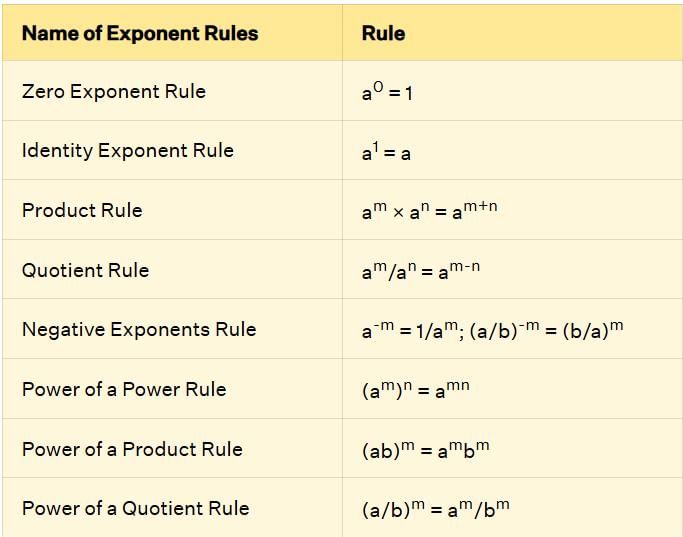
- The following rules help simplify expressions with exponents when the bases are the same.
1. Product Law
- When multiplying two powers with the same base, add the exponents: am × an = am+n.
- Steps:
- Identify the common base.
- Add the exponents of the terms.
- Write the result with the same base and the sum of exponents.
- Example: 33 × 35 = 33+5 = 38.
2. Quotient Law
- When dividing two powers with the same base, subtract the exponents.
- If m > n, then am ÷ an = am-n.
- If n > m, then am ÷ an = 1 ÷ an-m.
- Steps:
- Identify the common base.
- Subtract the exponent of the denominator from the numerator.
- If the result is positive, write it as am-n.
- If the result is negative, express it as 1 ÷ an-m.
- Example: 212 ÷ 27 = 212-7 = 25, and 26 ÷ 213 = 1 ÷ 213-6 = 1 ÷ 27.
3. Power Law
- When raising a power to another power, multiply the exponents: (am)n = am×n.
- Steps:
- Identify the base and the two exponents.
- Multiply the inner exponent by the outer exponent.
- Write the result with the same base and the product of exponents.
- Example: (35)2 = 35×2 = 310.
Behaviour of Negative Bases
- For a negative base -a:
- If the exponent n is even, (-a)n = an (positive).
- If the exponent n is odd, (-a)n = -an (negative).
- Steps:
- Determine if the exponent is even or odd.
- If even, the result is positive and equals an.
- If odd, the result is negative and equals -an.
- Example: (-2)4 = 16 (even exponent), (-2)5 = -32 (odd exponent).
Negative Integral Exponent
- For any non-zero rational number a, a negative exponent means the reciprocal: a-n = 1 ÷ an and an = 1 ÷ a-n.
- a-n and an are reciprocals of each other.
- Steps:
- If the exponent is negative, rewrite the expression as a fraction with a positive exponent in the denominator.
- If the expression is a fraction with a negative exponent, invert the fraction and make the exponent positive.
- Simplify the resulting expression.
- Example: 5-3 = 1 ÷ 53 = 1 ÷ 125, and (2/3)-5 = (3/2)5.
- For negative bases with negative exponents:
- Rewrite as 1 ÷ (-a)n.
- Evaluate (-a)n based on whether n is even or odd.
- Simplify the fraction.
- Example: (-2)-5 = 1 ÷ (-2)5 = 1 ÷ (-32) = -1/32.
More about exponents
1. (a × b)n = an × bn.
- Steps:
- Identify the product of bases inside the parentheses.
- Apply the exponent to each base separately.
- Write the result as the product of the bases raised to the exponent.
- Example: (a5 × b-3)4 = (a5)4 × (b-3)4 = a20 × b-12, and (34 × 5-3)-2 = 3-8 × 56.
2. (a ÷ b)n = an ÷ bn.
- Steps:
- Identify the fraction inside the parentheses.
- Apply the exponent to the numerator and denominator separately.
- Write the result as a fraction with the numerator and denominator raised to the exponent.
- Example: (a-3 ÷ b4)6 = (a-3)6 ÷ (b4)6 = a-18 ÷ b24, and (57 ÷ 3-4)-3 = 5-21 ÷ 312.
3. a0 = 1 for any non-zero a.
- Steps:
- Any non-zero number raised to the power zero is 1.
- Verify that the base is not zero.
- Example: 50 = 1, (-8)0 = 1.
4. a-m = 1 ÷ am and 1 ÷ a-m = am for non-zero a.
- Steps:
- Rewrite negative exponents as reciprocals with positive exponents.
- Simplify the expression.
- Example: 2-3 = 1 ÷ 23 = 1 ÷ 8, 1 ÷ 5-7 = 57.
5. Root notation: √[n]{a} = a1/n and √[n]{am} = am/n.
- Steps:
- Express the root as a fractional exponent.
- Simplify the exponent if possible.
- Example: √5 = 51/2, √[6]{57} = 57/6.
- For negative bases:
- If m is even, (-a)m = am.
- If m is odd, (-a)m = -am.
- Example: (-5)4 = 54 = 625, (-5)3 = -53 = -125.
The document Chapter notes: Exponents (Powers) | Mathematics Class 8 ICSE is a part of the Class 8 Course Mathematics Class 8 ICSE.
All you need of Class 8 at this link: Class 8
|
23 videos|98 docs|14 tests
|
FAQs on Chapter notes: Exponents (Powers) - Mathematics Class 8 ICSE
| 1. What are exponents and how are they used in mathematics? |  |
Ans. Exponents, or powers, are a way to express repeated multiplication of a number by itself. For example, 2^3 (read as "two to the power of three") means 2 × 2 × 2, which equals 8. They are used to simplify expressions and make calculations easier, particularly when dealing with large numbers.
| 2. What are the laws of exponents? |  |
Ans. The laws of exponents are rules that simplify calculations involving powers. Some key laws include:
1) a^m × a^n = a^(m+n) (Multiplication of same bases),
2) a^m ÷ a^n = a^(m-n) (Division of same bases),
3) (a^m)^n = a^(m*n) (Power of a power), and
4) a^0 = 1 (Any non-zero number raised to the power of zero is one).
| 3. What does a negative integral exponent mean? |  |
Ans. A negative integral exponent indicates that the base should be taken as the reciprocal. For example, a^-n equals 1/(a^n). This means that if you have a number with a negative exponent, you can convert it to a positive exponent by taking the reciprocal of the base raised to the corresponding positive exponent.
| 4. How can I simplify expressions involving exponents? |  |
Ans. To simplify expressions with exponents, apply the laws of exponents systematically. Combine like terms by using multiplication and division rules, convert negative exponents to positive by taking reciprocals, and simplify any powers of powers. For example, 2^3 × 2^2 can be simplified to 2^(3+2) = 2^5 = 32.
| 5. Why is it important to understand exponents in mathematics? |  |
Ans. Understanding exponents is crucial as they are a foundational concept in mathematics, used in various fields such as algebra, science, and engineering. They allow for efficient representation of large numbers, simplification of calculations, and are essential in understanding concepts like scientific notation, polynomials, and functions.
Related Searches















