Class 8 Exam > Class 8 Notes > Mathematics Class 8 ICSE > Chapter notes: Special Types of Quadrilaterals
Chapter notes: Special Types of Quadrilaterals | Mathematics Class 8 ICSE PDF Download
| Table of contents |

|
| Introduction |

|
| Trapezium |

|
| Parallelogram |

|
| Rectangle |

|
| Rhombus |

|
| Square |

|
Introduction
Quadrilaterals are four-sided polygons with unique properties that make them interesting to study. This chapter explores special types of quadrilaterals, including trapeziums, parallelograms, rectangles, rhombuses, and squares. Each type has distinct features, such as parallel sides, equal sides, or right angles, which define their shapes and properties. By understanding these quadrilaterals, their theorems, and their characteristics, we can solve geometric problems and prove relationships between their sides, angles, and diagonals. The chapter provides clear definitions, theorems, and conditions to identify and prove these shapes, making geometry both logical and engaging.
Trapezium
- A quadrilateral with one pair of opposite sides parallel is called a trapezium.
- The parallel sides are called bases, and the non-parallel sides are called legs.
- An isosceles trapezium is a special type where the non-parallel sides (legs) are equal in length.
- In an isosceles trapezium:
- Opposite angles next to the bases are equal (e.g., ∠A = ∠B and ∠C = ∠D).
- The diagonals are equal in length (e.g., AC = BD).
- Example: In an isosceles trapezium ABCD, side AB is parallel to side DC, and non-parallel sides AD and BC are equal. This means ∠A = ∠B, ∠C = ∠D, and diagonal AC equals diagonal BD.

Parallelogram
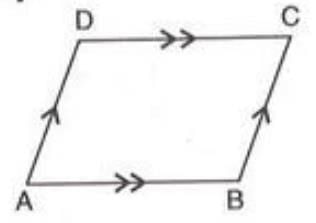
- A quadrilateral with both pairs of opposite sides parallel is called a parallelogram.
- Key properties of a parallelogram:
- Opposite sides are equal in length (e.g., AB = DC and AD = BC).
- Opposite angles are equal (e.g., ∠A = ∠C and ∠B = ∠D).
- Each diagonal divides the parallelogram into two congruent triangles.
- Theorem 2: Properties of a Parallelogram
- Statement:In a parallelogram ABCD:
- Opposite sides are equal (AB = DC and AD = BC).
- Opposite angles are equal (∠A = ∠C and ∠B = ∠D).
- Each diagonal bisects the parallelogram (triangles ABC and ADC are congruent, and triangles ABD and BCD are congruent).
- Construction: Draw diagonal AC.
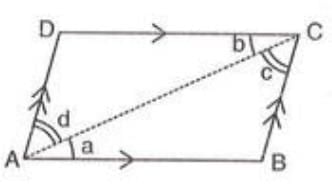
- Proof Steps:
- In triangles ABC and ADC:
- ∠a = ∠b (alternate angles, as AC cuts parallel sides AB and DC).
- ∠c = ∠d (alternate angles, as AC cuts parallel sides AD and BC).
- AC = AC (common side).
- Therefore, triangle ABC is congruent to triangle ADC by ASA (Angle-Side-Angle).
- Thus, AB = DC, AD = BC (corresponding sides of congruent triangles).
- ∠A = ∠C, ∠B = ∠D (corresponding angles of congruent triangles).
- Triangles ABC and ADC are equal, so diagonal AC bisects the parallelogram.
- Similarly, by drawing diagonal BD, triangles ABD and BCD are congruent, proving BD bisects the parallelogram.
- Statement:In a parallelogram ABCD:
- Example: In parallelogram ABCD, prove that consecutive angles are supplementary.
- Since AB is parallel to DC and AD is parallel to BC, opposite angles are equal (∠A = ∠C, ∠B = ∠D). The sum of all angles in a quadrilateral is 360°. Thus, ∠A + ∠B + ∠C + ∠D = 360°. Substituting ∠A = ∠C and ∠B = ∠D, we get 2(∠A + ∠B) = 360°, so ∠A + ∠B = 180°. Hence, consecutive angles are supplementary.
- Theorem 3: Diagonals Bisect Each Other
- Statement: In a parallelogram ABCD, the diagonals intersect at point O, and OA = OC, OB = OD.
- Proof Steps:
- In triangles AOB and COD:
- ∠a = ∠b (alternate angles).
- ∠c = ∠d (alternate angles).
- AB = DC (opposite sides of a parallelogram).
- Therefore, triangle AOB is congruent to triangle COD by ASA.
- Thus, OA = OC and OB = OD (corresponding parts of congruent triangles).
- Example: In parallelogram ABCD, the diagonals intersect at O. If OB = 6 cm and AC is 6 cm more than BD, find OC.
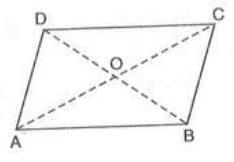
- Since diagonals bisect each other, OB = 6 cm implies BD = 12 cm. Given AC = BD + 6 = 18 cm, OC = 1/2 × AC = 9 cm.
- Theorem 4: Opposite Sides Equal and Parallel
- Statement: If a quadrilateral ABCD has AB = DC and AB parallel to DC, it is a parallelogram.
- Construction: Join points B and D.
- Proof Steps:
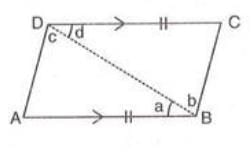
- In triangles ABD and CDB:
- AB = DC (given).
- BD = BD (common).
- ∠a = ∠d (alternate angles, as BD cuts parallel sides AB and DC).
- Therefore, triangle ABD is congruent to triangle CDB by SAS (Side-Angle-Side).
- Thus, ∠C = ∠b (corresponding angles).
- Since ∠C and ∠b are alternate angles, AD is parallel to BC.
- Since both pairs of opposite sides (AB, DC and AD, BC) are parallel, ABCD is a parallelogram.
- Example: In parallelogram ABCD, X and Y are points on diagonal BD such that DX = BY. Prove that AXCY is a parallelogram.
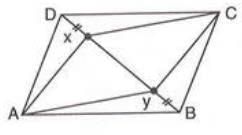
- In triangles ADX and CBY, AD = BC (opposite sides), DX = BY (given), and ∠ADX = ∠CBY (alternate angles). Thus, triangles ADX and CBY are congruent by SAS, so AX = CY. Similarly, triangles CDX and ABY are congruent, so CX = AY. Since AX = CY and CX = AY, AXCY is a parallelogram (opposite sides equal).
- Conditions to Prove a Quadrilateral is a Parallelogram:
- Opposite sides are parallel.
- Opposite sides are equal.
- Opposite angles are equal.
- Diagonals bisect each other.
- One pair of opposite sides is equal and parallel.
Rectangle
- A quadrilateral with opposite sides equal, parallel, and all angles equal to 90° is called a rectangle.
- Key properties:
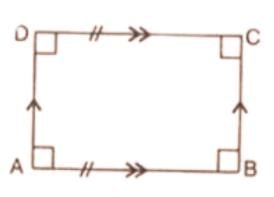
- Opposite sides are equal (AB = DC, AD = BC).
- Opposite sides are parallel (AB || DC, AD || BC).
- Each angle is 90° (∠A = ∠B = ∠C = ∠D = 90°).
- Ways to Prove a Quadrilateral is a Rectangle:
- Show each angle is 90°.
- Show it is a parallelogram with one angle equal to 90°.
- Show it is a parallelogram with equal diagonals.
- Example: In rectangle ABCD, diagonals AC and BD intersect at O. If OA = 2x + 6 and OD = 3x + 3, find x.
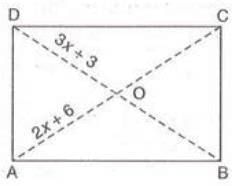
- Since diagonals of a rectangle are equal and bisect each other, OA = OD. Thus, 2x + 6 = 3x + 3, solving gives x = 3.
Rhombus
- A quadrilateral with all sides equal is called a rhombus.
- Key properties:
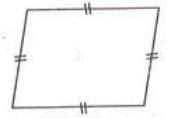
- All sides are equal (AB = BC = CD = DA).
- Opposite sides are parallel (like a parallelogram).
- Ways to Prove a Quadrilateral is a Rhombus:
- Show all sides are equal.
- Show diagonals bisect each other at 90°.
- Ways to Prove a Parallelogram is a Rhombus:
- Show diagonals intersect at 90°.
- Show any pair of adjacent sides is equal.
- Example: In rhombus ABCD, one diagonal BD equals its sides. Find the angles.
- Since AB = BC = CD = DA = BD, triangles ABD and BCD are equilateral. Thus, ∠A = ∠C = 60°. Since consecutive angles are supplementary, ∠B + 60° = 180°, so ∠B = ∠D = 120°. Hence, angles are 60°, 120°, 60°, 120°.
Square
- A quadrilateral with all sides equal and all angles 90° is called a square.
- Key properties:
- All sides are equal (AB = BC = CD = DA).
- Each angle is 90° (∠A = ∠B = ∠C = ∠D = 90°).
- Diagonals bisect each other at 90°.
- Diagonals are equal.
- Ways to Prove a Quadrilateral is a Square:
- Show all sides are equal and each angle is 90°.
- Show diagonals bisect each other at 90° and are equal.
- Ways to Prove a Parallelogram is a Square:
- Show all sides are equal.
- Show each angle is 90°.
- Show diagonals are equal.
- Show diagonals intersect at 90°.
- Ways to Prove a Rectangle is a Square:
- Show adjacent sides are equal.
- Show diagonals intersect at 90°.
- Ways to Prove a Rhombus is a Square:
- Show each angle is 90°.
- Show diagonals are equal.
- Properties: A square has all properties of a quadrilateral, trapezium, parallelogram, rectangle, and rhombus.
- Example: In parallelogram ABCD, the bisectors of angles A and D intersect at P. Prove ∠APD = 90°.
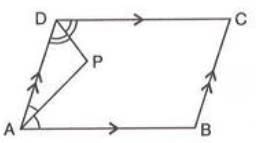
- Since AB || DC and AD is a transversal, ∠BAD + ∠ADC = 180°. AP bisects ∠BAD, so ∠PAD = 1/2 ∠BAD. DP bisects ∠ADC, so ∠PDA = 1/2 ∠ADC. Thus, ∠PAD + ∠PDA = 1/2 (∠BAD + ∠ADC) = 90°. In triangle APD, ∠PAD + ∠PDA + ∠APD = 180°, so ∠APD = 180° - 90° = 90°.
The document Chapter notes: Special Types of Quadrilaterals | Mathematics Class 8 ICSE is a part of the Class 8 Course Mathematics Class 8 ICSE.
All you need of Class 8 at this link: Class 8
|
23 videos|98 docs|14 tests
|
FAQs on Chapter notes: Special Types of Quadrilaterals - Mathematics Class 8 ICSE
| 1. What is a trapezium and how is it different from other quadrilaterals? |  |
Ans. A trapezium, also known as a trapezoid in some regions, is a four-sided figure (quadrilateral) with at least one pair of parallel sides. The main difference between a trapezium and other quadrilaterals like parallelograms, rectangles, rhombuses, and squares is that those shapes have more rigid properties, such as having two pairs of parallel sides or equal side lengths.
| 2. What are the properties of a parallelogram? |  |
Ans. A parallelogram is a type of quadrilateral where opposite sides are parallel and equal in length. The opposite angles are also equal, and the diagonals bisect each other. This means that if you draw the diagonals, they will cut each other in half.
| 3. How do you identify a rectangle among quadrilaterals? |  |
Ans. A rectangle can be identified by its properties: it has four right angles (90 degrees), and opposite sides are equal in length. Additionally, the diagonals of a rectangle are equal in length and bisect each other.
| 4. What is a rhombus and how does it differ from a square? |  |
Ans. A rhombus is a quadrilateral with all four sides of equal length, but it does not necessarily have right angles. In contrast, a square is a special type of rhombus that has both equal sides and four right angles. Therefore, while all squares are rhombuses, not all rhombuses are squares.
| 5. Can you explain the characteristics of a square? |  |
Ans. A square is a special type of quadrilateral that has all sides equal in length and all angles equal to 90 degrees. Additionally, the diagonals of a square are equal in length, bisect each other at right angles, and are also equal. A square is both a rectangle and a rhombus due to its properties.
Related Searches















