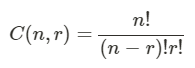Theory
Suppose if Ajay and Vijay from the earlier example did not get along and could not picked together. In this case, we can consider three cases - one when Ajay is picked, one when Vijay is picked and one when neither is picked. The sum of these three cases is equal to the number of cases without condition - cases where they are picked together. Number of ways they can be picked together is 715 ways as seen earlier. Hence, number of ways in which at max only one of them is picked = 1365 - 715= 650 ways.

Formula
Selection without arrangement:
Choosing r out of n options can be represented as
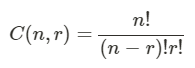
Tips
If the arrangement should always begin or end with a particular item, its order is fixed. Hence the remaining n-1 items can be arranged in (n-1)! ways.
Solved Example
Question for Cheatsheet: Permutation Combination Probability
Try yourself: How many 3 digit number can be formed with the digits 5, 6, 2, 3, 7 and 9 which are divisible by 5 and none of its digit is repeated?
Explanation
Answer – c) 20 Explanation : _ _ 5
first two places can be filled in 5 and 4 ways respectively so, total number of 3 digit number = 5*4*1 = 20
Report a problem
Question for Cheatsheet: Permutation Combination Probability
Try yourself: In how many different ways can the letter of the word ELEPHANT be arranged so that vowels always occur together?
Explanation
Answer – b) 2160 Explanation : Vowels = E, E and A. They can be arranged in 3!/2! Ways so total ways = 6!*(3!/2!) = 2160
Report a problem
Question for Cheatsheet: Permutation Combination Probability
Try yourself:A fruit basket contains 4 oranges, 5 apples and 6 mangoes. The number of ways a person make selection of fruits from among the fruits in the basket is?
Explanation
Whenever it is not explicity mentioned that fruit and distint, We take them as identical. 0 or more orange can be selected from 4 identical oranges in (4+1)=5 ways. 0 or more apples can be selected from 5 identical apples in (5+1)=6 ways.
0 or more mangoes can be selected from 6 identical mangoes in 7 ways.
∴ Total no. of ways in which all of three types of fruits can be selected (the no. of any type of fruits may also be 0),
5×6×7=210,
But in these 20 selection, there is one selection where all fruits are 0, hence we reduce 1 selection.
∴ the required no. =210−1=209
Report a problem
Question for Cheatsheet: Permutation Combination Probability
Try yourself:There are 15 points in a plane out of which 6 are collinear. Find the number of lines that can be formed from 15 points.
Explanation
Answer – c) 91 Explanation : From 15 points number of lines formed = 15c2 6 points are collinear, number of lines formed by these = 6c2 So total lines = 15c2 – 6c2 + 1 = 91
Report a problem
Question for Cheatsheet: Permutation Combination Probability
Try yourself:In how many ways 4 Indians, 5 Africans and 7 Japanese be seated in a row so that all person of same nationality sits together
Explanation
Answer – a) 4! 5! 7! 3!
Explanation : 4 Indians can be seated together in 4! Ways, similarly for Africans and Japanese in 5! and 7! respectively. So total ways = 4! 5! 7! 3!
Report a problem