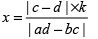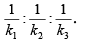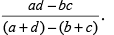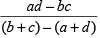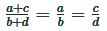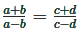Theory
Properties of Ratios
- A ratio need not be positive.
- However, if we are dealing with quantities of items, their ratios will be positive
- A ratio remains the same if both numerator and denominator are multiplied or divided by the same non-zero number, i.e.,
(i) a/b = pa/pb = qa/qb , where p, q ≠ 0
(ii) a/b = (a/p)/(b/p) , where p,q ≠ 0

Formula
(i) Two numbers are in the ratio of a : b. If both are increased/decreased by k then the ratio of the two numbers becomes c : d then the value x (H.C.F) is given by 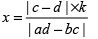
The two numbers will be ax and bx.
(ii) If the ratio of two numbers A and B is N1 : D1 and that of B and C is N2 : D2 then the ratio of three numbers i.e. A : B : C = ( N1 × N2) : (D1 × N2) : (D1 × D2).
(iii) Three numbers are such that k1 times the first number, k2 times the second number and k3 times the third number are all equal. then the three numbers are in the ratio of 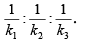
(iv) If two ratios a : b and c : d have equal values then a, b, c and d are said to be in proportion i.e. a : b = c : d. Here a and d are called the ends and b and c are called means of the proportion. In a proportion the product of extremes is equal to the product of the means.
⇒ a × d = b × c
(v) The number to be subtracted from each of a, b, c and d so that they become proportional is 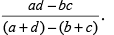
Similarly the least number to be added to each of a, b, c and d so that they became proportional is 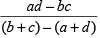
Tips
If a, b, c, d and x are positive integers such that a/b = c/d
Solved Example
Question for Cheatsheet: Ratio & Proportion
Try yourself:An amount of money is to be divided between P, Q and R in the ratio of 3:7:12.If the difference between the shares of P and Q is Rs.X, and the difference between Q and R’s share is Rs.3000. Find the total amount of money?
Explanation
To find the total amount of money divided between P, Q, and R in the ratio of 3:7:12:
Given:
- Let k be the common multiplier.
- P's share = 3k
- Q's share = 7k
- R's share = 12k
Equations:
- Difference between Q and P:
7k - 3k = 4k = X
- Difference between Q and R:
12k - 7k = 5k = 3000
Solve for k:
k = 3000 / 5 = 600
Calculate Shares:
- P's share = 3k = 1800
- Q's share = 7k = 4200
- R's share = 12k = 7200
Total Amount:
Total = 1800 + 4200 + 7200 = 13200
Report a problem
Question for Cheatsheet: Ratio & Proportion
Try yourself:If a certain amount X is divided among A, B, C in such a way that A gets 2/3 of what B gets and B gets 1/3 of what C gets, which of the following is true
Explanation
- A= (2/3) x B; B= (1/3) x C;
- Therefore , A/B = 2/3 and B/C = 1/3
- A:B = 2:3 ; B:C = 1:3;
- A:B:C = 2:3:9
- C = 9/14 x 1638 = 1053
Report a problem
Question for Cheatsheet: Ratio & Proportion
Try yourself:Seats for Mathematics, Science and arts in a school are in the ratio 5:7:8. There is a proposal to increase these seats by X%, Y% and Z% respectively. And the ratio of increased seats is 2:3:4, which of the following is true?
Explanation
- Ans– C
- For solving this question we need to use a hit and trial method
- As we approached option c, X = 40; Z = 75
- Number of increased seats are (140% of 5x), (150% of 7x) and (175% of 8x)
- i.e., (140/100 * 5x), (150/100 * 7x) and (175/100 * 8x)
- i.e., 7x, 21x/2 and 14x
- Required ratio = 7x : 21x/2 : 14x
- = 14x : 21x : 28x
- = 2 : 3 : 4
Report a problem
Question for Cheatsheet: Ratio & Proportion
Try yourself:A company manufactures three products: A, B, and C. The production ratio of A, B, and C is 3:5:7. The total production of these three products together in a month is 30,000 units. How many units of each product were produced?
Explanation
The given ratio is:
A : B : C = 3 : 5 : 7
Let the common factor be x. Thus, the production units will be:
A = 3x
B = 5x
C = 7x
We are also given that the total production is 30,000 units. So:
3x + 5x + 7x = 30,000
15x = 30,000
x = 2,000
Now, substitute x = 2,000 into the expressions for each product:
A's production = 3 × 2,000 = 6,000 units
B's production = 5 × 2,000 = 10,000 units
C's production = 7 × 2,000 = 14,000 units
So, the production for A, B, and C is:
A = 6,000 units
B = 10,000 units
C = 14,000 units
Final Answer:
Initial production:
A = 6,000 units, B = 10,000 units, C = 14,000 units
Report a problem
Question for Cheatsheet: Ratio & Proportion
Try yourself:Two candles of the same height are lighted at the same time. The first is consumed in 4 hours and the second in 3 hours. Assuming that each candle burns at a constant rate, in how many hours after being lighted was the first candle twice the height of the second?
Explanation
Report a problem