Circles Class 9 Notes Maths Chapter 10
What is a Circle?
- Any closed shape with all points connected at equidistance from centre forms a Circle.
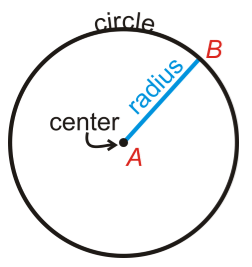
- Any point which is at equidistance from anywhere from its boundary is known as the Centre of the Circle.
- Radius is a Latin word which means ‘ray' but in the circle it is the line segment from the centre of the Circle to its edge. So any line starting or ending at the centre of the circle and joining anywhere on the border on the circle is known as the Radius of Circle.
Interior and Exterior of a Circle
In a flat surface, the interior of a circle is the line whose distance from the centre is less than the radius. The exterior of a circle is the line in the plane whose distance from the centre is larger than the radius.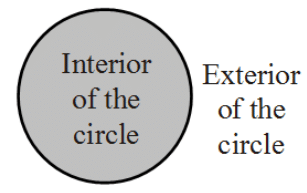
Terms Related to Circle
- Chord: Any straight line segment that’s both endpoints falls on the boundary of the circle is known as Chord. In Latin, it means ‘bowstring’.
- Diameter: Any straight line segment or Chord which passes through the centre of the Circle and its endpoints connects on the boundary of the Circle is known as the Diameter of Circle. So in a circle Diameter is the longest chord possible in a circle.
- Arc: Any smooth curve joining two points is known as Arc. So in Circle, we can have two possible Arcs, the bigger one is known as Major Arc and the smaller one is known as Minor Arc.
- Circumference: It is the length of the circle if we open and straightened out to make a line segment.
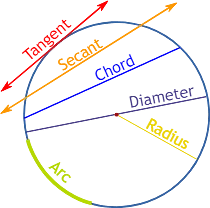
Segment and Sector of the Circle
- A segment of the circle is the region between either of its arcs and a chord. It could be a major or minor segment.
- Sector of the circle is the area covered by an arc and two radii joining the centre of the circle. It could be the major or minor sector.

Angle Subtended by a Chord at a Point
If in a circle AB is the chord and is making ∠ACB at any point of the circle then this is the angle subtended by the chord AB at a point C.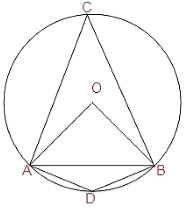
Likewise, ∠AOB is the angle subtended by chord AB at point O i.e. at the centre and ∠ADB is also the angle subtended by AB at point D on the circle.
Theorem 1: Any two equal chords of a circle subtend equal angles at the centre.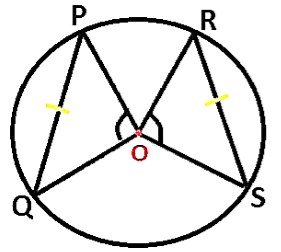
Here in the circle, the two chords are given and PQ = RS with centre O.
So OP = OS = OQ = OR (all are radii of the circle)
∆POQ ≅ ∆SOR
∠POQ = ∠SOR
This shows that the angles subtended by equal chords to the centre are also equal.
Theorem 2: If the angles made by the chords of a circle at the centre are equal, then the chords must be equal.
Theorem 2 is the reverse of the Theorem 1.
Perpendicular from the Centre to a Chord
Theorem 3: If we draw a perpendicular from the centre of a circle to any chord then it bisects the chord.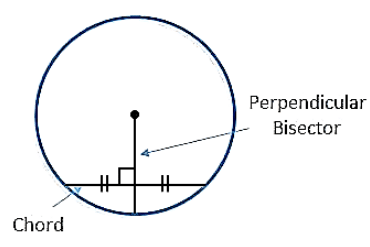
If we draw a perpendicular from the centre to the chord of the circle then it will bisect the chord. And the bisector will make 90° angle to the chord.
Theorem 4: The line which is drawn from the centre of a circle to bisect a chord must be perpendicular to the chord.
If we draw a line OB from the centre of the circle O to the midpoint of the chord AC i.e. B, then OB is the perpendicular to the chord AB.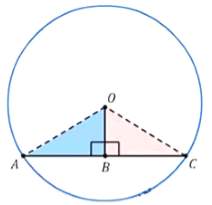
If we join OA and OC, then
In ∆OBA and ∆OBC,
AB = BC (B is the midpoint of AC)
OA = OC (Both are the radii of the same circle)
OB = OB (same side)
Hence, ΔOBA ≅ ΔOBC (both are congruent by SSS congruence rule)
⇒ ∠OBA = ∠OBC (respective angles of congruent triangles)
∠OBA + ∠OBC = ∠ABC = 180° [Linear pair]
∠OBC + ∠OBC = 180° [Since ∠OBA = ∠OBC]
2 x ∠OBC = 180°
∠OBC = 90o
∠OBC = ∠OBA = 90°
∴ OB ⊥ AC
Circle through Three Points
Theorem 5: There is one and only one circle passing through three given non-collinear points.
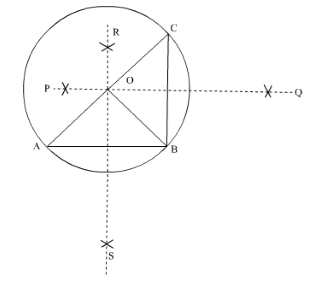
In this figure, we have three non-collinear points A, B and C. Let us join AB and BC and then make the perpendicular bisector of both so that RS and PQ the perpendicular bisector of AB and BC respectively meet each other at Point O.
Now take the O as centre and OA as the radius draw the circle which passes through the three points A, B and C.
This circle is known as Circumcircle. Its centre and radius are known as the Circumcenter and Circumradius.
Equal Chords and Their Distances from the Centre
Theorem 6: Two equal chords of a circle are at equal distance from the centre.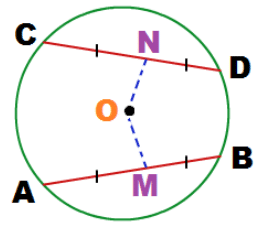
AB and CD are the two equal chords in the circle. If we draw the perpendicular bisector of these chords then the line segment from the centre to the chord is the distance of the chord from the centre.
If the chords are of equal size then their distance from the centre will also be equal.
Theorem 7: Chords at equal distance from the centre of a circle are also equal in length. This is the reverse of the above theorem which says that if the distance between the centre and the chords are equal then they must be of equal length.
Angle Subtended by an Arc of a Circle
The angle made by two different equal arcs to the centre of the circle will also be equal.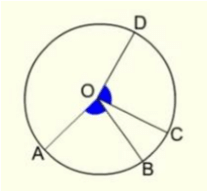
There are two arcs in the circle AB and CD which are equal in length.
So ∠AOB = ∠COD.
Theorem 8: The angle subtended by an arc at the centre is twice the angle subtended by the same arc at some other point on the remaining part of the circle.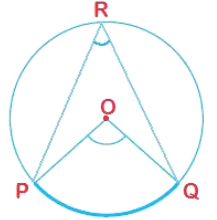
In the above figure ∠POQ = 2∠PRQ.
Theorem 9: Angles from a common chord which are on the same segment of a circle are always equal.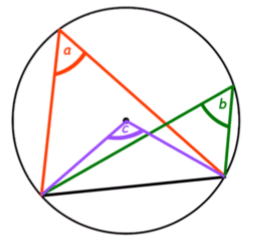
If there are two angles subtended from a chord to any point on the circle which are on the same segment of the circle then they will be equal.
∠a = (1/2) ∠c (By theorem 8)
∠b = (1/2) ∠c
∠a = ∠b
Cyclic Quadrilaterals
If all the vertex of the quadrilateral comes on a circle then it is said to be a cyclic quadrilateral.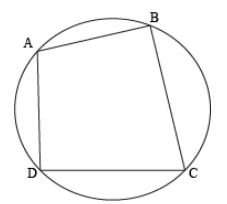
Theorem 10: Any pair of opposite angles of a cyclic quadrilateral has the sum of 180º.
∠A + ∠B + ∠C + ∠D = 360º (angle sum property of a quadrilateral)
∠A + ∠C = 180°
∠B + ∠D = 180º
Theorem 11: If the pair of opposite angles of a quadrilateral has sum of 180º, then the quadrilateral will be cyclic.
Theorem 11 is the reverse of the theorem 10.
|
40 videos|471 docs|57 tests
|
















