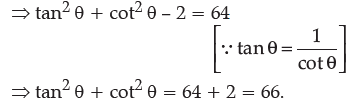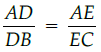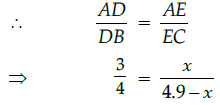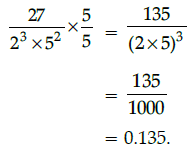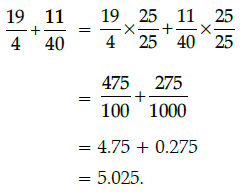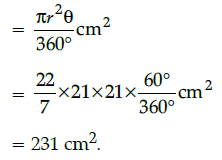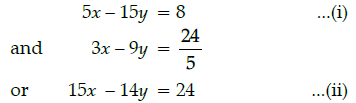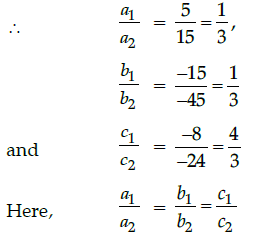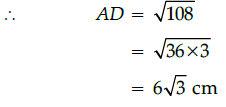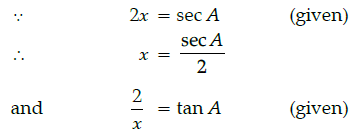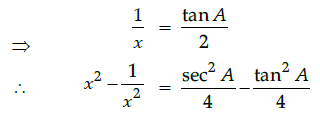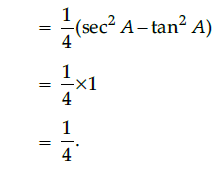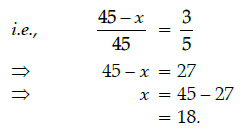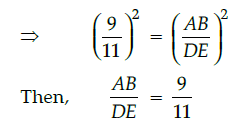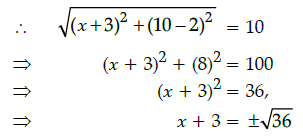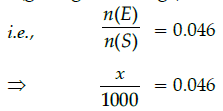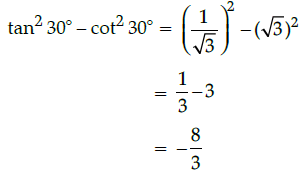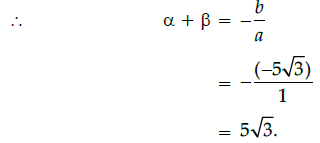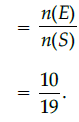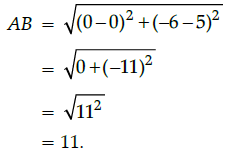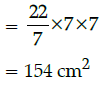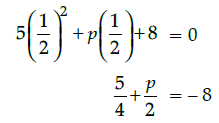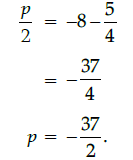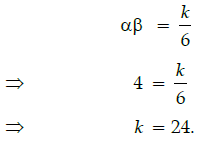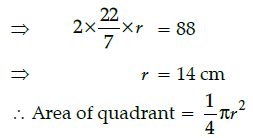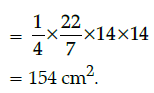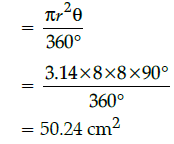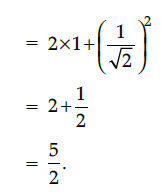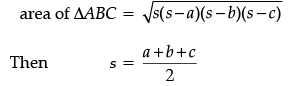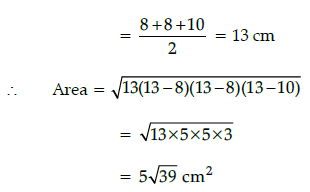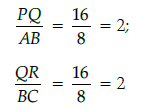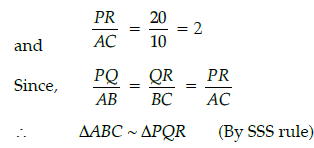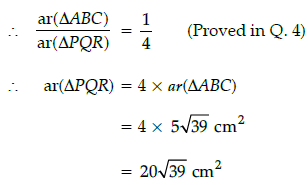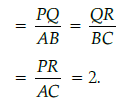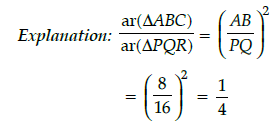Class 10 Mathematics: CBSE Sample Question Paper- Term I (2021-22) - 3 | Mathematics (Maths) Class 10 PDF Download
Class-X
Time: 90 Minutes
M.M: 40
General Instructions:
- The question paper contains three parts A, B and C.
- Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Q.1: The smallest number which when divided by 28 and 42 leaves remainders 8 and 22 respectively is:
(a) 104
(b) 84
(c) 64
(d) 74
Correct Answer is Option (c)
∵ 28 – 8 = 20 and 42 – 22 = 20
Now, 28 = 22 × 7
and 42 = 2 × 3 × 7
∴ LCM (28, 42) = 22 × 3 × 7
= 84
Required number = LCM (28, 42) – 20
= 84 – 20
= 64.
Q.2: If tan θ – cot θ = 8, then the value of tan2θ + cot2θ is:
(a) 68
(b) 69
(c) 66
(d) 70
Correct Answer is Option (c)
Given,
tan θ – cot θ = 8
Taking square on both sides, we get
tan2 θ + cot2 θ – 2 tan q . cot θ = 64
Q.3: In the given figure, 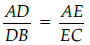 and ∠AED = ∠ABC, then :
and ∠AED = ∠ABC, then :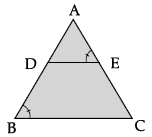
(a) ∠B = ∠C
(b) ∠A = ∠D
(c) ∠A = ∠E
(d) ∠A = ∠B
Correct Answer is Option (a)
Here,
So, DE || BC [By the converse of Thales theorem]
∴ ∠AED = ∠ACB
(corresponding angles)
But ∠AED = ∠ABC (given)
∴ ∠ABC = ∠ACB.
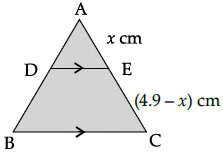
Q.4: In a given DABC, DE || BC and AB/DB = 3/4. If AC = 4.9 cm, then AE is :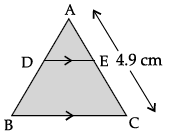
(a) 2.5 cm
(b) 2.8 cm
(c) 2.1 cm
(d) 2.6 cm
Correct Answer is Option (c)
Let AE = x cm,
then EC = (4.9 – x) cm
and DE || BC (given)
⇒ 3(4.9 – x) = 4x
⇒ 14.7 – 3x = 4x
⇒ 7x = 14.7
⇒ x = 2.1
Q.5: If p(– 3) = 0, then one factor of the polynomial p(x) is:
(a) x – 3
(b) x + 3
(c) 3x
(d) x/3
Correct Answer is Option (b)
∵ p(– 3) = 0
∴p(x) = x + 3.
Q.6: The decimal expansion of the rational number 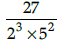 will terminate after:
will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Correct Answer is Option (c)
Q.7: If the short and long hands of a clock are 5 cm and 6 cm long respectively, then the distance travelled by long hand in 60 hours is:
(a) 32π cm
(b) 28π cm
(c) 60π cm
(d) 96π cm
Correct Answer is Option (c)
∵ Long hand makes 5 rounds in 60 hours and radius of the circle formed by long hand = 6 cm
∴ Distance travelled by long hand in 5 rounds
= 5 × circumference of the circle
= 5 × 2πr
= 5 × 2π × 6
= 60π cm.
Q.8: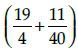 as a decimal fraction is:
as a decimal fraction is:
(a) 5.025
(b) 4.485
(c) 4.575
(d) 4.285
Correct Answer is Option (a)
Q.9: There is a circular playground having radius 21cm to be constructed. Then the engineers decided to construct a minor sector for open gym which as shown in the below figure, which is OACBO. Then find the area of sector OACBO.
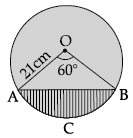
(a) 221 cm2
(b) 231 cm2
(c) 866 cm2
(d) 235 cm2
Correct Answer is Option ()
Here, r = 21 cm, θ = 60°
∴ Area of the sector OACBO
Q.10: The graphs of the equations 5x – 15y = 8 and 3x – 9y = 24/5 are two lines which are:
(a) coincident
(b) parallel
(c) perpendicular to each other
(d) intersecting exactly at one point
Correct Answer is Option (a)
Hence, both lines are coincident.
Q.11: From a pack of 52 cards, Jacks, queens, kings and aces of black colour are removed. From the remaining, a card is drawn at random, then the probability that the card drawn is a ten; is:
(a) 1/22
(b) 3/22
(c) 1/11
(d) 10/11
Correct Answer is Option (c)
No. of removed cards = 2 + 2 + 2 + 2
∴ Remaining cords = 52 – 8 = 44
i.e., n(S) = 44
and no. of tens cards = 4
i.e., favourable outcomesn(E) = 4
Q.12: If x = (22 × 32 × 73) and y = (23 × 33 × 72), then HCF (x, y) =
(a) 1760
(b) 1752
(c) 1754
(d) 1764
Correct Answer is Option (d)
HCF (x, y) = Product of common terms
with lowest power
= 22 × 32 × 72
= 1764
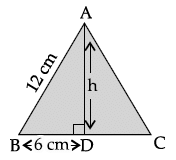
Q.13: If in an equilateral triangle of side 12 cm, then the length of the altitude is:
(a) 4√3 cm
(b) 6√3 cm
(c) 5√3 cm
(d) 7√3 cm
Correct Answer is Option (b)
Here, ABC is an equilateral triangle of side 12 cm.
Let the length of the altitude be h cm and BD is 6 cm.
In right angled DADB,
(AD)2 = (AB)2 – (BD)2
(By using Pythagoras theorem)
= (12)2 – (6)2
= 144 – 36
= 108
Q.14: If 2x = sec A and 2/x = tan A, then the value of x2 - 1/x2 is:
(a) 1/2
(b) 1/4
(c) 1/3
(d) 1
Correct Answer is Option (b)
Q.15: A jar contains 45 marbles. Some of these are white and others are yellow. If a marble is drawn at random from the jar, the probability that it is white is 3/5, then the number of yellow marbles in the jar is:
(a) 18
(b) 27
(c) 25
(d) 20
Correct Answer is Option (a)
Total outcomes,
n(S) = 45
Let the number of yellow marbles be x,
then the no. of white marbles = 45 – x.
Given, P(getting a white marble) = 3/5
Q.16: DABC ~ DDEF such that ar(DABC) = 81 cm2 and ar(DDEF) = 121 cm2, then the ratio of their corresponding sides is:
(a) 3 : √11
(b) 9 : 11
(c) 11 : 9
(d) √9 : √11
Correct Answer is Option (b)
Since DABC ~ DDEF, we have
Hence, the ratio of the corresponding sides is 9 : 11.
Q.17: The sum of the ages of a father and the son is 45 years. If father's age is four times that of his son, then son's age is:
(a) 7 years
(b) 8 years
(c) 9 years
(d) none of these
Correct Answer is Option (c)
Let age of father and son be x and y respectively, then
x + y = 45 ...(i)and x = 4y ...(ii)
Substituting x = 4y in eq. (i), we get
4y + y = 45
⇒ 5y = 45
⇒ y = 9
Q.18: If the distance between the points A(– 3, 2) and B(x, 10) is 10, then the possible values of x is:
(a) 3 and 9
(b) - 3 and 9
(c) 3 and - 9
(d) - 3 and -9
Correct Answer is Option (c)
Taking positive sign, x = 6 – 3 = 3
Taking negative sign, x = – 6 – 3 = – 9.
Q.19: The probability of getting a bad orange in a lot of 1000 is 0.046. The number of bad oranges in the lot is:
(a) 46
(b) 48
(c) 41
(d) 50
Correct Answer is Option (a)
Total oranges,
n(S) = 1000
Let the no. of bad oranges be x, then
n(E) = x
P(getting bad orange) = 0.046
⇒ x = 1000 × 0.046⇒ x = 46.
Q.20: The value of tan2 30° – cot2 30° is:
(a) - 1
(b) - 2
(c) -8/3
(d) -1/3
Correct Answer is Option (c)
Section - B
Q.21: If two positive integers p and q are written as p = a2b3 and q = a3b3, where a and b are prime numbers, then LCM (p, q) × HCF (p, q) is :
(a) a2b4
(b) a4b5
(c) a3b4
(d) a5b6
Correct Answer is Option (d)
In case of assertion:
p = a2 b3
and q = a3 b3
Then LCM (p, q) = a3 b3
and HCF (p, q) = a2 b3
∴LCM (p, q) × HCF (p, q)
= a3 b3 × a2 b3
= a5 b6.
Q.22: If α and β are the zeroes of a polynomial x2 – 5√3x + 6, then α + β:
(a) 4√3
(b) 5√3
(c) 2√3
(d) 3√3
Correct Answer is Option (b)
Let x2 – 5√3x + 6= 0
Q.23: If cosec θ . cos θ = 1, then the value of q is:
(a) 30°
(b) 60°
(c) 90°
(d) 45°
Correct Answer is Option (d)
cosec θ . cos θ = 1
⇒ cot θ = 1
= cot 45°
⇒ θ = 45°
Q.24: 19 cards numbered 1, 2, 3, ....., 19 are put in a box and mixed thoroughly. A man draws a card from the box, then the probability (getting the no. on the card is odd) is:
(a) 9/19
(b) 8/19
(c) 7/19
(d) 10/19
Correct Answer is Option (d)
Total outcomes n(S) = 19
odd numbered cards = 1, 3, 5, 7, 9, 11, 13,
15, 17, 19
i.e., favourable outcomes
n(E) = 10
∴ P(getting a card is odd)
Q.25: One zero of the polynomial 2x3 - x2 - 13x - 6 is:
(a) -8
(b) 3
(c) -3
(d) 1
Correct Answer is Option (b)
Let p(x) = 2x3 – x2 – 13x – 6, then 3 is a
zero of p(x).
∴ p(x) = 0
i.e., p(3) = 2(3)3 – (3)2 – 13(3) – 6
= 2 × 27 – 9 – 39 – 6
= 54 – 9 – 45 = 0
Q.26: Reema wanted to go her school after covid-19, before go to her school, She wanted to calculate the total distance between her house and school from the adjacent diagram.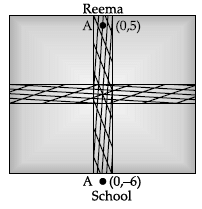
(a) 61
(b) 61
(c) √62
(d) √62
Correct Answer is Option (c)
Here, x1 = 0, y1 = 5 and x2 = 0, y2 = - 6
So, distance between A(0, 5) and B(0, -6):
Q.27: The distance of the point (7, 5) from x-axis is:
(a) 7
(b) - 7
(c) - 5
(d) 5
Correct Answer is Option (d)
Since y-coordinate of a given point is the distance of point from x-axis, then the distance of the point (7, 5) from x-axis is 5.
Q.28: If the circumference of a circle is 14π, then the area of the circle is:
(a) 160 cm2
(b) 154 cm2
(c) 170 cm2
(d) 180 cm2
Correct Answer is Option (d)
Circumference = 14π
⇒ 2pr = 14π
⇒ r = 7 cm
Then area of the circle = πr2
Q.29: Mr. Shayam has recently shifted in his new house. When he entered in master bed room and observed its dimensions 8m × 6m × 4m. He decided to put one longest rod into it. The length of the longest rod will be.
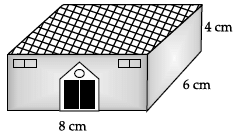
(a) 4 m
(b) 6 m
(c) 2 m
(d) 12 m
Correct Answer is Option (c)
Length = 8 m, breadth = 6 m and height = 4 m
Since, the length of the longest rod is equal to HCF (8, 6 and 4), i.e.,
8 = 23,
6 = 2 × 3
and 4 = 22
Then, HCF (8, 6 and 4) = 2
Thus, the longest rod that can measure
the dimensions of the room exactly = 2m.
Q.30: The value of 10 sec2 A – 10 tan2 A is:
(a) 9
(b) 10
(c) 11
(d) 12
Correct Answer is Option (b)
10 sec2 A – 10 tan2 A = 10 (sec2 A – tan2 A)
= 10 × 1
[∵ sec2 q – tan2 q =1]
= 10.
Q.31: The value of the quadratic polynomial f(x) = 2x2 - 3x - 2 at x = 1 is:
(a) - 2
(b) - 1
(c) - 4
(d) - 3
Correct Answer is Option (d)
Given,
f(x) = 2x2 - 3x - 2
Then, f(1) = 2(1)2 - 3(1) -– 2
= 2 - 3 - 2
= -3.
Q.32: In a lottery, there are 8 prizes and 16 blanks. The probability of getting a prize is:
(a) 1/2
(b) 2/3
(c) 1/3
(d) 5/3
Correct Answer is Option (c)
In case of assertion,
Total no. of lottery tickets
= 8 + 16 = 24
∴ P(getting a prize) = 8/24 = 1/3
Q.33: If one zero of the quadratic polynomial 5x2 + p(x) + 8 = 0 is 1/2, then the value of p is:
(a) 33/2
(b) 35/2
(c) - 37/2
(d) 41/2
Correct Answer is Option (c)
5x2 + p(x) + 8 = 0
∵ 1/2 is a zero, so it must satisfy the given equation,
Q.34: If the product of the zeros of the quadratic polynomial 6x2 – 5x + k is 4, then the value of k is:
(a) 24
(b) 20
(c) 22
(d) 26
Correct Answer is Option (a)
Let the zeroes of the given quadratic polynomial be α and β, so we have
Q.35: If cosec θ . cos θ = 1, then the value of q is:
(a) 30°
(b) 60°
(c) 90°
(d) 45°
Correct Answer is Option (d)
cosec θ . cos θ = 1
⇒ cot θ = 1
= cot 45°
⇒ θ = 45°
Q.36: If the circumference of a circle is 88 cm, then the area of a quadrant of a circle is:
(a) 77 cm2
(b) 77/8 cm2
(c) 154 cm2
(d) 308 cm2
Correct Answer is Option (c)
Circumference,
2πr = 88 cm
Q.37: If one zero of the quadratic polynomial x2 – 3x – k is – 1, then the value of k is:
(a) 2
(b) 3
(c) 4
(d) 6
Correct Answer is Option (c)
Let p(x) = x2 – 3x – k
∵ -1 is a zero of p(x), then
p(–1) = 0
∴ (-1)2 - 3(-1) - k = 0
⇒ 1 + 3 - k = 0
⇒ k = 4.
Q.38: If a chord of the circle of radius 8 cm subtends a right angle at the centre, then the area of sector OACBO is: (Use, p = 3.14)
(a) 50.24 cm2
(b) 45.24 cm2
(c) 48.25 cm2
(d) 50.28 cm2
Correct Answer is Option (a)
Here, r = 8 cm and θ = 90°
Then, area of sector OACBO
Q.39: If x + 5 is a factor of p(x) = 2x3 – 4x2 + ax + 5, then the value of a is:
(a) - 4
(b) - 3
(c) 4
(d) 3
Correct Answer is Option (a)
x + 5 = 0
⇒ x = – 5
∴ 2(- 5)3 - 4(- 5)2 + a(- 5) + 5 = 0
⇒ 2 x (-125) - 100 - 5a + 5 = 0
⇒ - 350 + 5 = 5a
⇒ 5a = - 345
⇒ a = - 69
Q.40: If tan θ = cot θ, then the value of 2 tan θ + cos2 θ is:
(a) 1
(b) 2
(c) 3
(d) 5/2
Correct Answer is Option (d)
∵ tan θ = cot θ
Here tan 45° = cot 45°
= 1.
∴ θ = 45°
Now 2 tan θ + cos2 θ = 2 tan 45° + (cos45°)2
 |
Download the notes
Class 10 Mathematics: CBSE Sample Question Paper- Term I (2021-22) - 3
|
Download as PDF |
Section - C
Direction: Q. 41-Q.45 are based on case study-1
Case Study - 1
A Mathematics Exhibition is being conducted in your School and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.
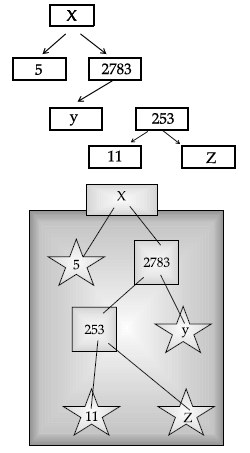
Q.41: What will be the value of z?
(a) 22
(b) 23
(c) 17
(d) 19
Correct Answer is Option (d)
From question (1),
Putting x = 33 is eq. (i), we get
33 + y = 83
⇒ y = 83 – 33 = 50.
Q.42: What will be the value of x?
(a) 15005
(b) 13915
(c) 56920
(d) 17429
Correct Answer is Option (c)
As we know,
∠A + ∠C = 180°
⇒ 2x – 1 + 2y + 15 = 180°
⇒ x + y = 83 ...(i)
∠B + ∠D = 180°
y + 5 + 4x – 7 = 180°
4x + y = 182 ...(ii)
Subtracting eq. (i) from (ii), we get
3x = 99
⇒ x = 33.
Q.43: The prime factorisation of 13915 is
(a) 5x 113 x 132
(b) 5x 113 x 232
(c) 5x 112 x 23
(d) 5x 112 x 232
Correct Answer is Option (a)
∠B + ∠C = (y + 5)° + (2y + 15)°
= (3y + 20)°
= (3 × 50° + 20°)
= 170°.
Q.44: What will be the value of y?
(a) 23
(b) 22
(c) 11
(d) 19
Correct Answer is Option (b)
∠A + ∠D = (2x – 1)° + (4x – 7)°
= (6x – 8)°
= (6 × 33 – 8)°
[From question (i), x = 33]
Q.45: According to Fundamental Theorem of Arithmetic 13915 is a
(a) Composite number
(b) Prime number
(c) Neither prime nor composite
(d) Even number
Correct Answer is Option (c)
∠D = (4x – 7)°
= (4 × 33 – 7)°
= 125°.
Direction: Q. 46-Q.50 are based on case study-2
Case Study - 2
Due to heavy storm, many electric wire got bend and many broke. Mr. Prabhakar observed the shape of a bent wire in front of his house. He then draws its shape in a graph as shown below:
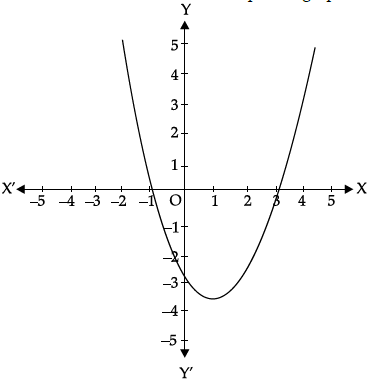
Q.46: The zeroes of the polynomial are:
(a) - 1, 5
(b) - 1, 3
(c) 3, 5
(d) - 4, 2
Correct Answer is Option (b)
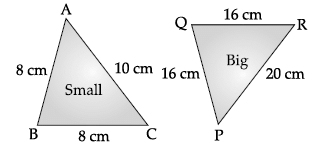
By using Heron's formula,
∴ Total area of small pizza
= 4 × Area of one slice
= 4 × 5√39
= 20√39 cm2
Q.47: The shape in which wire is bent, is:
(a) spiral
(b) ellipse
(c) linear
(d) parabola.
Correct Answer is Option (c)
Let ABC and PQR represent the slice of smaller and bigger pizza, then in DABC and DPQR,
Q.48: What is the value of polynomial, if x = 2 ?
(a) 3
(b) 0
(c) - 6
(d) - 3
Correct Answer is Option (b)
Now, total area of bigger pizza= 3 × area of one slice
= 3 × 20√39 cm2
= 60√39 cm2
Q.49: How many zeroes are there for the polynomial, shape of the wire ?
(a) 2
(b) 3
(c) 1
(d) 0
Correct Answer is Option ()
When two triangles are similar the reduced ratio of any two corresponding sides is called the scale factor, so scale factor
Q.50: What will be the expression of the polynomial ?
(a) x2 + 2x + 3
(b) x2 – 2x + 3
(c) x2 – 2x – 3
(d) x2 + 2x – 3
Correct Answer is Option (a)
|
127 videos|551 docs|75 tests
|