Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry

Q1: If cotθ = 7/8 then what is the value of 
Sol: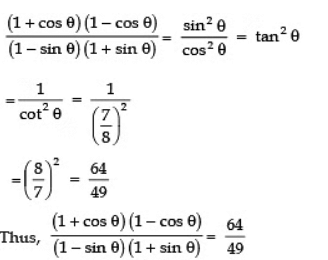  

Q2: If tan A   then find sin A.
Sol: In a right Δ ABC (∠B = 90°), Hypotenuse = AC, Base = AB, and Perpendicular = BC.
Since,

Using Pythagoras theorem, we have:

Q3: Evaluate cos 60°· sin 30° + sin 60°· cos 30°.
Sol: We have:

cos 60°· sin 30° + sin 60°· cos 30°

Q4: In the given figure, AC is the length of a ladder. Find it.

Sol: Let AC =x = [Length of ladder]
∴ In right Δ ABC,

Thus, the length of the ladder is 2√3 m.

Q5: If sin θ = 12/13 , find the value of:  .
Sol: 

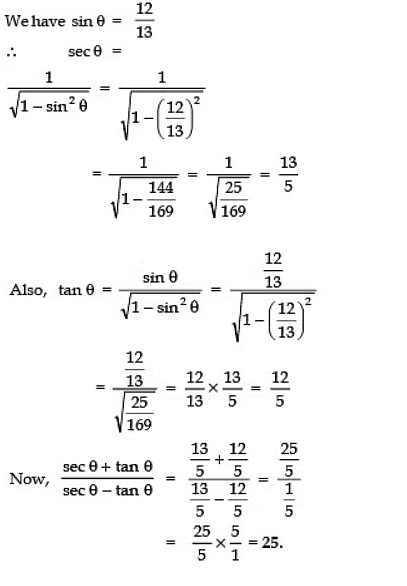Q6: In the given figure, find BC.

Sol: In Δ ABC,

Q7: In Δ ABC, if AD ⊥ BC and BD = 10 cm; ∠ B = 60° and ∠C = 30°, then find CD.
Sol: In right Δ ABD, we have

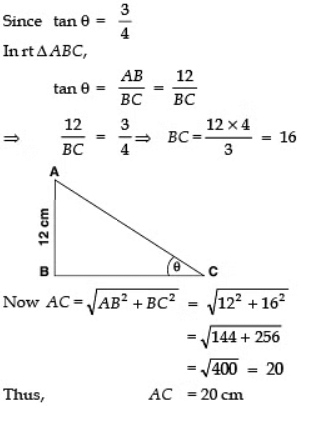
Q8: In the given figure,   find AC, if AB = 12 cm.
Sol: 

Q9: In the given figure, Δ ABC is a right triangle. Find the value of 2 sinθ − cosθ.
 Sol: We have the right Δ ABC,

Q10: In the figure, find sinA.
Sol: In right Δ ABC,

Q11: Find the value of:

Sol: We have:

Q12: Write the value of:  
Sol: 

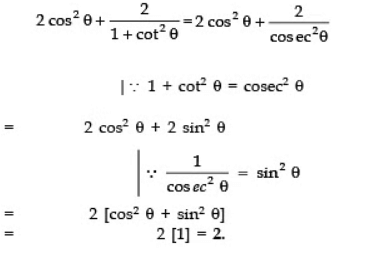
Q13: Write the value of:  
Ans:

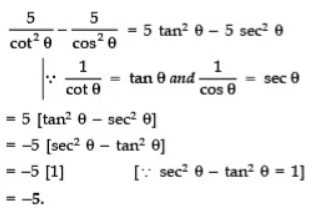
Q14: If sec² θ (1 + sin θ) (1 − sinθ) = k, find the value of k.
Sol:

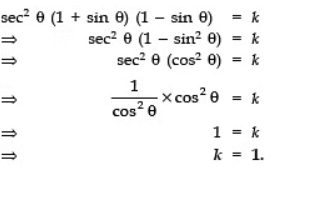
Q15: If sin   then find the value of (2 cot² θ + 2).
Sol: 2 cot² θ + 2 = 2 (cot² θ + 1) = 2 (cosec² θ)

Q16: If cos A = 3/5, find 9 cot² A − 1.

Q17: If tan θ = cot (30° + θ ), find the value of θ.
Sol: We have:
tan θ = cot (30° + θ)
= tan [90° − (30° + θ)]
= tan [90° − 30° − θ]
= tan (60° − θ)
⇒ θ = 60° − θ
⇒ θ + θ = 60°

Q18: If sinθ = cosθ, find the value of θ.

Sol: We have:
sinθ = cosθ
Dividing both sides by cosθ, we get

⇒ tan θ = 1 ...(1)
From, the table, we have:
tan 45° = 1 ...(2)
From (1) and (2), we have:
θ = 45°.

Q19: If tan A = cot B, prove that A + B = 90°.
Sol: Since tan A = cot B
   ∴ tan A = tan (90°-B)
⇒ A = 90°-B
⇒ A + B = 90°. [Hence proved] 

Q20: If sin 3θ = cos (θ – 6)° and 30 and (θ – 6)° are acute angles, find the value of θ.
Sol: We have:
sin 30 = cos (θ – 6)°
= sin [90°- (θ – 6)°]
[∵ sin (90° – θ) = cos θ]
⇒ 3θ = 90° – (θ – 6)°
⇒ 3θ = 90 – θ + 6
⇒ 3θ + θ = 96
⇒ 4θ = 96
⇒ θ = = 24
Thus θ = 24°.