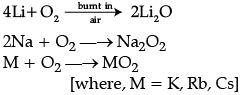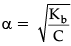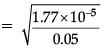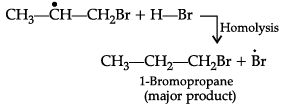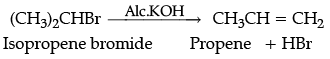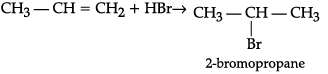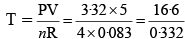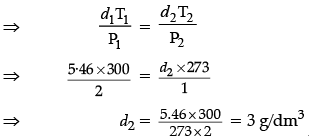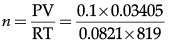Class 11 Chemistry: CBSE Sample Question Papers- Term II (2021-22)- 2 | Sample Papers for Class 11 Medical and Non-Medical - JEE PDF Download
| Table of contents |

|
| Class Xl |

|
| Time: 120 Minutes |

|
| Max. Marks: 35 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class Xl
Time: 120 Minutes
Max. Marks: 35
General Instructions:
- There are 12 questions in this question paper with internal choice.
- Section A: Q. No. 1 to 3 are very short answer questions carrying 2 marks each.
- Section B: Q. No. 4 to 11 are short answer questions carrying 3 marks each.
- Section C: Q. No. 12 is case based question carrying 5 marks.
- All questions are compulsory.
- Use of log tables and calculators is not allowed.
Section - A
Q.1. Attempt any two:
(i) Define physical equilibrium. Give an example also.
(ii) Define chemical equilibrium. Give an example.
(iii) Why is chemical equilibrium called dynamic equilibrium?
(i) A physical equilibrium is a system whose physical state does not change when dynamic equilibrium is reached.
e.g., Solid ↔ Liquid.
(ii) A chemical equilibrium is a system whose chemical composition of the system does not change when dynamic equilibrium is reached.
e.g., N2(g) + 3H2(g) ↔ 2NH3(g)
(iii) Chemical equilibrium is achieved when the rate of forward and backward reaction becomes equal. Although overall it is in equilibrium but inside the forward reaction and backward reaction both occur and so there is motion in the atomic and molecular level. Dynamic refers to anything having motion. Since, the equilibrium is not static so, the chemical equilibrium is called dynamic equilibrium.
Q.2. Out of the two pairs of compounds given below, identify the compound in each of the pairs which has Group 13 element in more stable oxidation state. Mention the nature of bonding too.
(i) TlCl3, TlCl
(ii) AlCl3, AlCl
(i) TlCl has more stable oxidation state than TlCl3 because on moving down the group due to inert pair effect, lower oxidation state is more stable. TlCl is ionic in nature.
(ii) AlCl3 has more stable oxidation state than AlCl because it does not display inert pair effect. Anhydrous state of AlCl3 is covalent while its aqueous state is ionic in nature.
Q.3. Give reasons to support your answer:
(i) Alkali metals should be stored in kerosene oil.
(ii) Lithium is kept wrapped in paraffin wax and not stored in kerosene.
(i) The alkali metals tarnish in air due to the formation of oxide at their surface and hence they are stored in kerosene oil.
(ii) Lithium cannot be stored in kerosene as it floats on the surface of kerosene because of its low density. Therefore, lithium is generally kept wrapped in the paraffin wax.
Section - B
Q.4. Account for the following:
(i) The hydroxides and carbonates of sodium and potassium are easily soluble in water while the corresponding salts of magnesium and calcium are sparingly soluble in water.
(ii) Potassium and caesium rather than lithium are used in photoelectric cells.
(iii) Lithium is a strong reducing agent in aqueous solution.
(i) The solubility of a salt in water depends upon their lattice energy and hydration energy.
In the case of hydroxide and carbonates of sodium and potassium, their hydration energy is more than their lattice energy. Therefore, they dissolve in water. In the case of hydroxides and carbonates of magnesium and calcium, their hydration energy is less than their lattice energy. Therefore, they are sparingly soluble.
(ii) Due to low ionisation enthalpy, potassium and caesium eject electrons when exposed to light while lithium has the highest ionisation enthalpy due to which it cannot be used in photoelectric cells.
(iii) The ionic size of lithium is small so it has highest hydration enthalpy. Ionisation energy of Li is highest among alkali metals but hydration enthalpy predominates over ionisation enthalpy, Thus, lithium has strong reducing power in aqueous solution.
OR
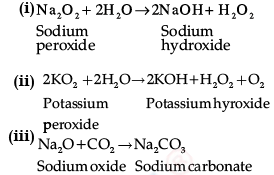
Write balanced equations for chemical reactions between the following:
(i) Na2O2 and water
(ii) KO2 and water
(iii) Na2O and CO2
Q.5. Answer the following questions:
(i) Under what conditions is the heat absorbed by a system is equal to the work done by the system?
(ii) Under what conditions the following reaction will be spontaneous:
(a) Reaction with both ΔH and ΔS positive.
(b) Reaction with both ΔH and ΔS negative.
By First law of thermodynamics ,
ΔU = q + w(i) For an ideal gas, undergoing an isothermal change, ∆U = 0. Hence, q = – W
i.e., the heat absorbed by the system is equal to work done by the system.
(ii)
(a) If ΔG = ΔH – TΔS <0, then reaction is spontaneous.
Then, the reaction will be spontaneous, if TΔS > ΔH.
Therefore, the reaction with both ΔH and ΔS positive will be spontaneous at sufficiently high temperature.
(b) If both ΔH and ΔS are negative, that means – TΔS will become positive and the reaction will be spontaneous at low temperature, where, ΔG will be negative.
ΔG = – ΔH + TΔS <0
OR
(i) What is enthalpy change at constant volume? Explain.
(ii) Calculate the enthalpy of transition for carbon from the following data given:
Cdiamond + O2 → CO2(g); ΔH = – 94·3 kcal
Camorphous + O2 → CO2(g); ΔH = – 97·6 kcal
Also calculate the heat required to change 1 g of Cdiamond to Camorphous.
(i) When reaction is carried out in a closed vessel so that volume remains constant, i.e., ΔV = 0, then qv = ΔU or ΔH = ΔU. This is known as enthalpy change at constant volume.
(ii) Heat of transition of Cdiamond to Camorphous Cdiamond + O2 → CO2(g)
ΔH = – 94·3 kcal ...(1)
Camorphous + O2 → CO2(g)
ΔH = – 97·6 kcal ...(2)
Subtract equation (2) from (1), we get
Cdiamond – Camorphous = – 94·3 – (– 97·6) = 3·3 kcal
This heat represents the transformation of 1 mole Cdiamond to Camorphous.Therefore, heat of transformation for 1 g of Cdiamond to 1 g Camorphous = 3·3 k cal/12 = 0·275 kcal
Q.6. Account for the following:
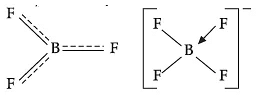
(i) BCl3 is more stable as compared to TlCl3.
(ii) Boron trifluoride behaves as a Lewis acid.
(iii)The B–F bond lengths in BF3 (130 pm) and BF4– (143 pm) differ.
(i) Thallium and boron belong to group 13 of the periodic table and +1 oxidation state becomes more stable as we move down the group. Boron is more stable than thallium because +3 state of thallium is highly oxidising and it reverts back to more stable +1 state.
(ii) The electronic configuration of boron is ns2 np1. It contains three electrons in its valence shell. Thus, it can form only three covalent bonds which means there are only six electrons around boron and its octet remains incomplete. When a boron atom combines with three fluorine atoms, its octet remains incomplete. Therefore, boron trifluoride remains electron-deficient and acts as lewis acid.
(iii) The B–F bond length in BF3 is shorter than the B–F bond length in BF4−. BF3 is an electron-deficient species. With a vacant p-orbital on boron, the fluorine and boron atoms undergo pπ–pπ back-bonding to remove this deficiency. This imparts a double bond character to the B–F bond. This double-bond character causes the bond length to shorten in BF3 (130 pm). However, when BF3 coordinates with the fluoride ion, a change in hybridisation from sp2 (in BF3) to sp3 (in BF4−) occurs. Boron now forms 4σ bonds and the double-bond character is lost. This accounts for a B–F bond length of 143 pm in BF4− ion.
Q.7. Determine the degree of ionisation and pH of a 0.05 M of ammonia solution. The ionisation constant of ammonia is 1.77 × 10–5. Also calculate the ionisation constant of conjugate acid of ammonia.
Given, Kb = 1.77 × 10–5
C = 0.05 MThe ionisation of NH3 in water is represented by the equation:
where, α = Degree of ionisation
C = concentration of solution Ionisation constant of ammonia,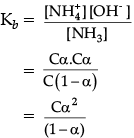
The value of α is small, so, the equation can be simplified by neglecting α in comparison to 1 in the denominator on right hand side of the equation.
∴ Kb = Cα2
or
= 0.018
[OH–] = Cα
= 0.05 × 0.018
= 9.4 × 10–4 M
∴ Ionisation product of water, [H+] [OH–] = Kwor
= 1.06 × 10–11M
Now pH = – log10 [H+]
= – log (1.06 × 10–11)
= – log 1.06 + 11 log 10
= – 0.0253 + 11= 10.9747
Now, using the relation for conjugate acid-base pair,Ka × Kb = Kw
Q.8. Observe the figure given below and answer the questions that follow:
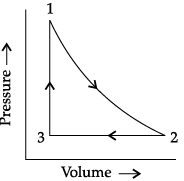 Pressure vs volume graph for a monoatomic ideal gas taken through a cycle of expansion and compression is shown in the figure.
Pressure vs volume graph for a monoatomic ideal gas taken through a cycle of expansion and compression is shown in the figure.
(i) What will be the value of ΔH for the cycle as a whole?
(ii) Define standard enthalpy of formation.
(iii) Define state function with examples.
(i) The value of ΔH for the cycle as a whole will be zero because it is a state function.
(ii) Standard enthalpy of formation (ΔfH°) is defined as the standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states of aggregation.
(iii) A state function is a property whose value does not depend on the path taken to reach that specific value. For example: Pressure volume, enthalpy change and internal energy.
Q.9. What happens when the following chemical reactions occur:
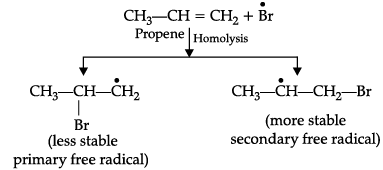
(i) HBr is added to propene in the presence of benzoyl peroxide.
(ii) Isopropyl bromide is treated with alc. KOH.
(i) Addition of HBr to unsymmetrical alkenes like propene in the presence of light or peroxide takes place following the Markovnikov's rule. This happens only with HBr but not with HCl and HI. Addition of HBr to propene in the presence of benzoyl peroxide follows anti-Markovnikov's rule or peroxide effect or Kharash effect.
Secondary free radicals are more stable than primary radicals. Thus, 1-bromopropane is obtained as the major product.
(ii) Dehydrohalogenation takes place.
OR
(i) Write IUPAC names of the following structural formula:
(a)
(b)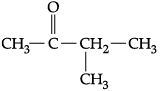
(ii) Complete the following chemical reactions:
(a) CH3—CH = CH2 + HBr→
(b) 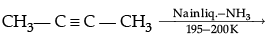
(i) (a) 2-methyl 1-butene
(b) 3-methyl- butan-2-one 1
(ii) (a) Electrophilic addition reaction is followed. By the Markonikov's rule, 2-bromopropane is formed as major product.
(b)
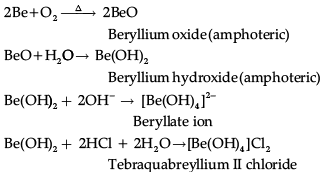
Q.10. An element of Group 2 in the Modern Periodic Table forms covalent oxide which is amphoteric in nature and dissolves in water to give an amphoteric hydroxide. Identify the element and write chemical reactions of the hydroxide of the element with an alkali and an acid.
Since the oxide formed from elements of Group 2 is amphoteric in nature so, the element is beryllium (Be).
Q.11. (i) Calculate the temperature of 4.0 moles of a gas occupying volume of 5 dm3 at pressure of 3.32 bar. [R = 0.083 bar dm3 K– 1 mol– 1]
(ii) Calculate the total number of electrons present in 1.4 g of dinitrogen gas.
(iii) Write the conditions in terms of temperature and pressure, under which all gases obey Charle’s law.
(i) Given,
P = 3.32 bar, V = 5 dm3
R = 0.083 bar dm3 K–1 mol–1
n = 4 molesBy Ideal gas equation,
PV = nRT
T = 50 K
(ii) No. of moles in 1.4 g of N2 gas = Given mass/Molar mass
= 1.4/28 = 1/20 = 0.05 mol
Total number of electrons present in 0.05 moles of N2,= 0.05 × 6.02 × 1023 × 14
= 4.214 × 1023 electrons 1
(iii) All gases obey Charle’s law at very low pressure and high temperature.
OR
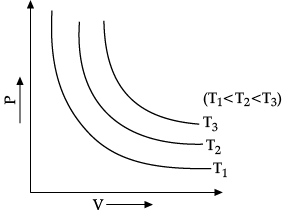
On the basis of the figure given below, answer the following questions: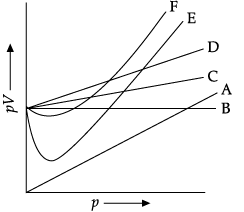 (i) Which curve in figure represents the curve of ideal gas?
(i) Which curve in figure represents the curve of ideal gas?
(ii) State the law followed by the curve B.
(iii) What are the conditions on the application of which a gas deviates from ideal behaviour?
(i) Curve B represents for ideal gas.
For ideal gas, pV = constant is represented by straight line. Therefore, only B represents the curve of ideal gas.
(ii) The ideal gas follows Boyle’s law.
For ideal gas, PV = constant represented by straight line. Therefore, Boyle’s law states that the pressure (p) of a given quantity of gas varies inversely with its volume (V) at constant temperature i.e., in mathematical expression, pV = k, a constant.
(iii) Gases deviate from ideal behaviour under high pressure and low temperatures because the intermolecular forces come into play as gas particles come close to each other by action of high pressure and low temperature.
Section - C
Q.12. Read the passage given below and answer the questions that follow:
Boyle’s law can be used to describe the effects of altitude on gases in closed cavities within the body, and to calculate the total intra-thoracic gas volume by body plethysmography. As altitude increases, ambient pressure decreases, and therefore, by Boyle’s law, volume expansion occurs in enclosed spaces. This effect can be demonstrated by observing the expansion of a sealed bag of potato chips on an ascending commercial flight. In one artificial pneumothorax model, a 40 mL pneumothorax increased in volume by up to 16% at 1.5 km (approx. 5000 feet) from sea level, an effect which may prompt thoracostomy before helicopter transfer to prevent transition to a tension pneumothorax. It is estimated that an expansion of up to 30% for a closed volume of gas in the human body, e.g., a bulla, can be expected after ascending from sea level to an altitude of 2.5 km (approx. 8200 feet).
Boyle's law also explains the use of saline in the cuff of an endotracheal tube during hyperbaric therapy; to prevent an air leak due to the reduction of volume as pressure increases. When ascending from depth, if a diver holds their breath, the gases in their lungs will expand and can cause barotrauma, arterial gas embolism, mediastinal emphysema, or even pneumothorax.
(i) How will you explain the expansion of a sealed packet of chips on a flight which is taking off?
(ii) When the graph of pressure is plotted against volume at different temperatures, a curve is obtained. Identify the curve that corresponds to the constant temperature.
(iii) What does the higher curves in the above mentioned graph correspond to? Explain with graphical representation?
(iv) Density of a gas is found to be 5.46 g/dm3 at 27°C, 2 bar pressure. What will be its density at STP condition?
(i) According to Boyle’s Law, PV= constant
As the flight takes off, altitude increases and the ambient pressure decreases resulting in expansion of volume in enclosed space of the chips packet.
(ii) P – V graph at different values of constant temperature are hyperbolic curve. The curves which correspond to constant temperature are called isotherms.
(iii) According to Boyle’s law
PV = k1
Graphically,Higher curves correspond to higher temperature. According to P – V diagram, for each curve value of k1 for each curve is different that vary with temperature only.
(iv) Given,
d1 = 5.46 g/dm3
d2 = ?T1 = (27 + 273)K = 300 K
At STP T2 = (0 + 273)K = 273 K
P1 = 2 barAt STP P2 = 1 bar
From Ideal gas equation,
d = PM/RTHence, density at STP condition is 3 g/dm3.
OR
34.05 mL of phosphorus vapours weigh 0.0625 g at 546°C and 0.1 bar pressure. What is the molar mass of phosphorus?
Given,
P = 0.1 barV = 34.05 ml=0.03405 L
R = 0.0821 Latm K-1 mol-1
T = 546 + 273 = 819 K
From ideal gas,
PV = nRT
=0.00005 mol = 5 × 10-5 mol
∴ Molar mass of phosphorus = Given mass/No. of moles
= 0.0625/0.00005
= 1250 g/mol
FAQs on Class 11 Chemistry: CBSE Sample Question Papers- Term II (2021-22)- 2 - Sample Papers for Class 11 Medical and Non-Medical - JEE
| 1. What is the duration of the Class Xl Chemistry exam? |  |
| 2. How many maximum marks can be obtained in the Class Xl Chemistry exam? |  |
| 3. How many sections are there in the Class Xl Chemistry exam? |  |
| 4. What is the purpose of Section A in the Class Xl Chemistry exam? |  |
| 5. What is the purpose of Section B in the Class Xl Chemistry exam? |  |