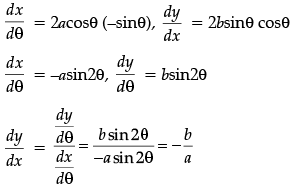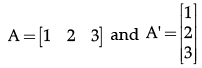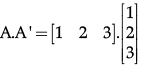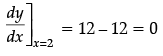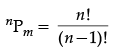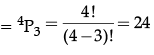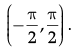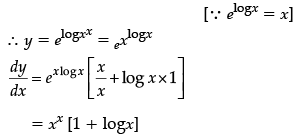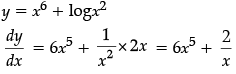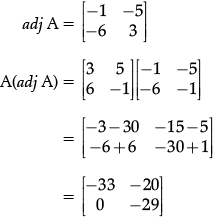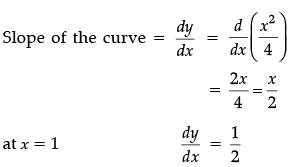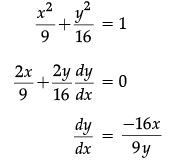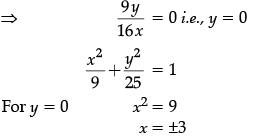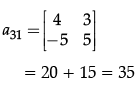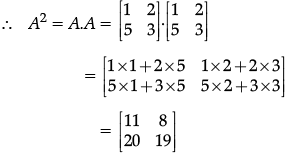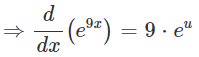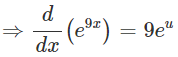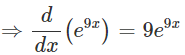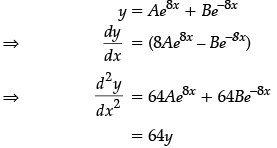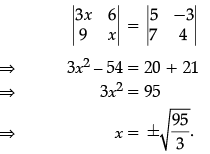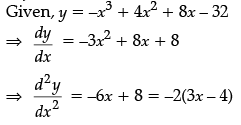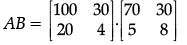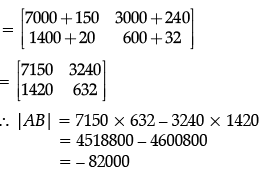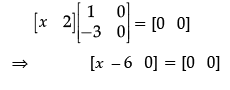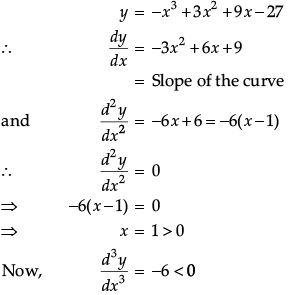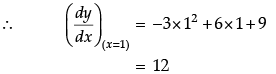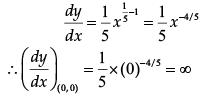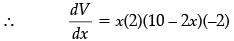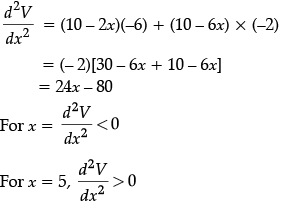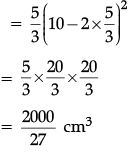Class 12 Mathematics: CBSE Sample Question Paper- Term I (2021-22)- 3 | Mathematics (Maths) Class 12 - JEE PDF Download
Class-XII
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three sections – A, B and C. Each part is compulsory.
- Section - A has 20 MCQs, attempt any 16 out of 20.
- Section - B has 20 MCQs, attempt any 16 out of 20.
- Section - C has 10 MCQs, attempt any 8 out of 10.
- There is no negative marking.
- All questions carry equal marks
Section - A
Q.1: What is the domain of the cos–1 x?
(a) [–∞, ∞]
(b) (–∞, ∞)
(c) (–1, 1)
(d) [–1, 1]
Correct Answer is Option (d)
The cosine function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. Now for the inverse of a function the domain becomes range and the range becomes domain. Thus the range of cosine function, that is, [-1,1] becomes the domain of inverse function.
Q.2: Find dy/dx where x = a cos2 θ and y = b sin2 θ.
(a) - b/α
(b) − b/α secθ
(c) − b/α tan θ
(d) − b/α cot θ
Correct Answer is Option (a)
x = αcos2 θ, y = bsin2θ
Q.3: Evaluate the determinant 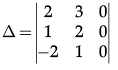
(a) 0
(b) 27
(c) –27
(d) 5
Correct Answer is Option (a)
If any one of the row or column of a square matrix has all elements as 0 then the determinant of the matrix is 0.
Q.4: If matrix A = [12 3]. Write A. A' where A' is the transpose of matrix A.
(a) 7
(b) 21
(c) 14
(d) 28
Correct Answer is Option (c)
A.A' = 1 + 4+ 9
A.A' = 14
Q.5: At what angle, the tangent to curve y = 3x2 − x3 at x = 2 makes with positive x-axis?
(a) 45°
(b) 0°
(c) 30°
(d) 60°
Correct Answer is Option (b)
y = 3x2 – x3
Slope = dy/dx = 6x – 3x2
Slope = tanθ
0 = tanθ
tan 0° = tanθ
θ = 0°
Q.6: For the given matrix , the values of y is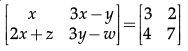
(a) x = 3
(b) x = 14
(c) y = 7
(d) y = –2
Correct Answer is Option (c)
Since corresponding entries of equal matrices are equal,
So x = 3 --------(1)
3x – y = 2 --------(2)
2x +z = 4 --------(3)
3y – w = 7 --------(4)
Put the value of x = 3 from equation 1 in equation 2
3x – y = 2
3(3) – y = 2
9 – y = 2
y = 9 – 2
y = 7
Q.7: Set A has 3 elements and set B has 4 elements. Then the number of injective mappings that can be defined from A to B is
(a) 144
(b) 12
(c) 24
(d) 64
Correct Answer is Option (c)
We know that, if A and B are two non-empty finite sets containing m and n elements, respectively, then
Number of one-one functions = nPm (if n≥m)
Number of one-one functions = 0
(if n < m)
So, by using the formula,
Number of one-one/ injective functions
Q.8: Find the minimum and maximum values of the given determinant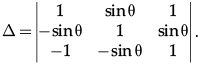
(a) 2 and 4
(b) –1 and 1
(c) 0 and 1
(d) –1 and 2
Correct Answer is Option (a)
The value of determinant comes out to be ∆ = 2 (1 + sin2 θ). As the minimum and maximum value of sin θ is known, it is manipulated according to the required equation.
-1 ≤ sin θ ≤ 1
0 ≤ sin2 θ ≤ 10 + 1 ≤ + sin2 θ ≤ 1 + 1
2 ≤ 2(1 + sin2 θ) ≤ 4
Q.9: Which of the function is continuous in R?
(a) log x
(b) sin x
(c) 3x2
(d) All of these
Correct Answer is Option (d)
Every polynomial function is continuous on R and every rational function is continuous on its domain. For Example: The constant function f(x) = 1 and the identity function g(x) = x are continuous on R.
Q.10: If a relation R on the set {1, 2, 3} be defined by R = {(1, 1)}, then R is
(a) reflexive
(b) transitive
(c) symmetric
(d) None of these
Correct Answer is Option (a)
R on the set {1, 2, 3} is defined by R = {(1, 1)} It is clear that R is reflexive.
Q.11: What is the principal value branch of tan–1 x ?
(a) 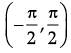
(b) [–1, 1]
(c) (–∞, ∞)
(d) 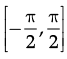
Correct Answer is Option (d)
The tangent function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. For tangent function this interval is considered as. Thus when we take the inverse of the function the domain becomes range and the range becomes domain. Hence the principal value branch is the range of tan-1 x , that is
Q.12: What is the derivative of 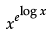 ?
?
(a) xx (1 + log x)
(b) log xe
(c) ex log x
(d) xe (1 + log x)
Correct Answer is Option (a)
Let y == xx
Q.13: Consider a square matrix 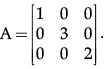 The given matrix is an example of
The given matrix is an example of
(a) Diagonal matrix
(b) Identity matrix
(c) Scalar matrix
(d) Null matrix
Correct Answer is Option (a)
A square matrix B = [bij] m × m is said to be a diagonal matrix if all its non diagonal elements are zero, that is a matrix B = [bij] m × m is said to be a diagonal matrix if bij = 0, when i ≠ j.
Q.14: If y = x6 + logx2 then the value of dy/dx is
(a) 6x5 – 2x
(b) 6x5 + 2/x
(c) 6x5 - 2/x
(d) 6x6 + x2
Correct Answer is Option (b)
Q.15: If 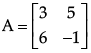 then |A αdj A| will be
then |A αdj A| will be
(a) 95
(b) 0
(c) 950
(d) 957
Correct Answer is Option (d)
∴ |A(αdj A)| = –33 × – 29 – 0
= 957
Q.16: Two numbers x and y related to each other as x – y = 3. What is the value of the numbers such that their product is minimum?
(a) x = 2.5, y = −0.5
(b) x = 1.5, y = −1.5
(c) x = 5.5, y = 2.5
(d) x = 1, y = −2
Correct Answer is Option (b)
On applying Second Derivative test, At x = 1.5 f '' (x) > 0
Q.17: Consider the curve y = x2/4. The Slope of the line parallel to tangent to the curve at x = 1 is
(a) 1/4
(b) 1/3
(c) - 1/2
(d) 1/2
Correct Answer is Option (d)
y = x2/4
Parallel lines have same slopes
∴ Slope of tangent = 1/2
Q.18: The points on the curve 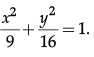 at which the tangents are parallel to y-axis.
at which the tangents are parallel to y-axis.
(a) (± 3, 0)
(b) (0, ± 3)
(c) (± 2, 0)
(d) (0, ± 2)
Correct Answer is Option (a)
∵ Tangent line is parallel to the y-axis.
⇒ Slope of the normal is 0
Hence, Points at which tangent are Parallel to the y-axis are (±3, 0).
Q.19: Objective functions
Maximise Z = 22x + 18y
Constraints : x + y ≤ 20
360x + 240y ≤ 5,760
Or 3x + 2y ≤ 48
x ≥ 0, y ≥ 0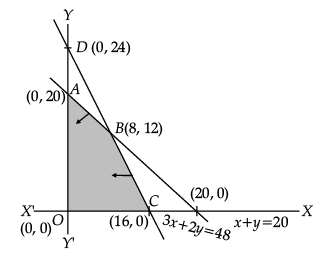
The maximum Z =
(a) 5,760
(b) 392
(c) 362
(d) 290
Correct Answer is Option (b)
Vertices of feasible region are : A(0, 20), B(8, 12), C(16, 0) & O(0, 0)Z(A) = 360, Z(B) = 392, Z(C) = 352
Max Z = 392
Q.20: Which of the following is true for the function f(x) = In x + 2 increasing.
(a) function is strictly increasing in (1,2).
(b) function is strictly decreasing in (1,2).
(c) function is constant in (1,2).
(d) None of the above
Correct Answer is Option (a)
First derivative is always positive in the given interval.
Section - B
Q.21: Let R be the relation in the set of integers Z given by R = {(a, b) : 3 divides a – b}. then R is:
(a) not reflexive
(b) reflexive
(c) symmetric
(d) transitive
Correct Answer is Option (a)
By definition, a relation in Z is said to be reflexive if xRx, ∀ x ∈ Z.
So, α – α = 0 ⇒ 3 divides α – α ⇒ αRa.
Hence R is reflexive.
Q.22: If f(x) = |x|, then the function is continuous but not differentiable at:
(a) x = 0
(b) x ¹ 0
(c) x = 1
(d) x = 2
Correct Answer is Option (a)
Given function is continuous but not differentiable at x = 0.
Q.23. A dietician wishes to mix together two kinds of food X and y in such a way that the mixture contains at least 15 units of carbohydrate, at least 17 units of protein and at most 6 units of fat. The nutrient contents of 1 kg food is given below:
1 kg of food X costs `16 and 1 kg of food Y cost `20. Find the least cost of the mixture which will produce the required diet.
(a) 100
(b) 128
(c) 110
(d) 99
Correct Answer is Option (a)
Let Food X be p and Food Y be q.
Formulate the constraints as per statement.
The Constraints are : p + 2q ≥ 15; 3p + 2q ≥ 17; p + < 6; p ≥ 0; q ≥ 0
And objective function is Z = 16p + 20q
By solving the above equations, Corner points will be (1, 7), (1, 5), (3, 4), (5, 1) and (0, 6) After putting these points in Z, we get the least cost of the mixture, i.e., 100.
Q.24. What is the domain of the cosec–1x ?
(a) [– ∞, ∞]
(b) (– ∞, ∞)
(c) (– 1, 1)
(d) (– ∞, – 1] ∪ [1, ∞)
Correct Answer is Option (d)
The cosec function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. Now for the inverse of a function the domain becomes range and the range becomes domain. Thus the range of cosec function, that is, (– ∞, – 1] ∪ [1, ∞) becomes the domain of inverse function.
Q.25. For a given matrix 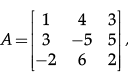 both the minor and cofactor of the element α31 is.
both the minor and cofactor of the element α31 is.
(a) 40
(b) 42
(c) 45
(d) 35
Correct Answer is Option (d)
Q.26: What is the derivative of 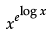 ?
?
(a) xx (1 + log x)
(b) log xe
(c) ex log x
(d) xe (1 + log x)
Correct Answer is Option (a)
Let y == xx
Q.27: Given a set A = {1, 2, 3} and R1 = {(1, 1), (1, 3), (3, 1), (2, 2), (2, 1), (3, 3)}; R2 = {(2, 2), (1, 3), (3, 1)}; and R3 = {(1, 3), (3, 3)}. Which of the following relations are equivalence relation?
(a) All of them
(b) R1, R3
(c) None of them
(d) R1
Correct Answer is Option (a)
R1 is reflexive but neither symmetric nor transitive. R2 is symmetric but neither reflexive nor transitive. R2 is transitive but neither reflexive nor symmetric.
Q.28: If A = 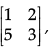 then A2 is:
then A2 is:
(a) 
(b)
(c) 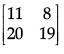
(d) 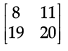
Correct Answer is Option (a)
Q.29: If y = e9x, then:
(a) y2 = 9e9x
(b) y2 = 81e
(c) y2 = 81e9x
(d) y2 = 81ex
Correct Answer is Option (a)
We have: e9x
This expression can be differentiated using the "chain rule".
Let u = 9x ⇒ u ' = 9 and v = eu ⇒ v ' = eu:
We can now replace u with 9x:
Q.30: The principal value of 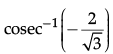 is:
is:
(a) π/3
(b) - π/3
(c) π/2
(d) -π/2
Correct Answer is Option (b)
The principal value ofmeans that we need to find an angle in the principal branch of the function where the cosec function is equal to -2/√3. Hence the required value is - π/3.
Q.31: If y = Ae8x + Be–8x, then d2y/dx2 is:
(a) 64y
(b) 8y
(c) –64y
(d) 40y
Correct Answer is Option (a)
Q.32: If  then the value of x is:
then the value of x is:
(a) 95/3
(b) 97/3
(c) 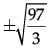
(d) 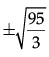
Correct Answer is Option (d)
Q.33: In which of the following, the constants of a linear function has to be maximized or minimized according to a set of given conditions
(a) Constraints
(b) Objective functions
(c) Decision variables
(d) Feasible solutions
Correct Answer is Option (b)
The objective function is a function in the LPP which is to be optimized. The LPP objective function either has maximum value or minimum value or has no solutions.
Q.34: If the curve y = –x3 + 4x2 + 8x – 32, then d2y/dx2 is
(a) –2(3x + 4)
(b) 2(3x + 4)
(c) –2(3x – 4)
(d) 2(3x – 4)
Correct Answer is Option (a)
Q.35: Let 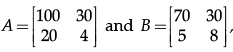 then |AB| is :
then |AB| is :
(a) 4600
(b) 5600
(c) 82000
(d) –82000
Correct Answer is Option (d)
Q.36: The principal value of cot−1 (√3) is:
(a) π/6
(b) - π/6
(c) π/3
(d) - π/3
Correct Answer is Option (a)
The principal value of cot−1(√3) means that we need to find an angle in the principal branch of the function where the cotangent function is equal to √3. Hence the required value is π/6.
Q.37: Let W be the set of words in the English dictionary. A relation R is defined on W as R = {(x, y) ∈ W × W such that x and y have at least one letter in common}. Then R is:
(a) Symmetric but not reflexive
(b) Both Symmetric and reflexive
(c) Reflexive but not symmetric
(d) Symmetric and transitive
Correct Answer is Option (b)
For any word x ∈ W, x and x have at least one (all) letter in common Therefore, (x, x) ∈ R,
⇒ x ∈ W so R is reflexive.Symmetric : Let (x, y) ∈ R, xy ∈ w
⇒ x and y have at least one letter in common
⇒ y and x have at least one letter in common
⇒ (y, x) ∈ R So, R is symmetric.
Q.38: Let two matrices be A = [2] and B =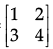 then A + B:
then A + B:
(a) 32
(b) 40
(c) 42
(d) A + B = not possible
Correct Answer is Option (d)
Matrix A is of Order |X| and B is of order 2×2. Hence, as per property of matrices, Addition can’t be operated on the given two matrices of different order.
Q.39: d/dx(sin 3x) at x = π/3 is:
(a) 0
(b) 1
(c) 2
(d) –3
Correct Answer is Option (d)
Q.40: If 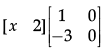 = 0, then x is:
= 0, then x is:
(a) 0
(b) 6
(c) –6
(d) –2
Correct Answer is Option (b)
Comparing the elements of both sides,
x – 6 = 0
x = 6.
Section - C
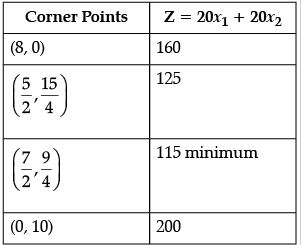
Q.41: Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 2, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20.
The minimum value of Z occurs at :
(a) (8, 0)
(b) 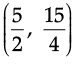
(c) (0, 10)
(d) 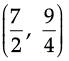
Correct Answer is Option (c)
Q.42: Maximum slope of the curve y = –x3 + 3x2 + 9x – 27 is:
(a) 0
(b) 12
(c) 16
(d) 32
Correct Answer is Option (b)
Given that,
So, the maximum slope of given curve is at x = 1.
Q.43: The curve y = x1/5 has at (0, 0)
(a) a vertical tangent (parallel to y-axis)
(b) a horizontal tangent (parallel to x-axis)
(c) an oblique tangent
(d) no tangent
Correct Answer is Option (a)
Given that, y =x1/5 On differentiating with respect to x, we get
So, the curve y = x1/5 has a vertical tangent at (0, 0), which is parallel to y-axis.
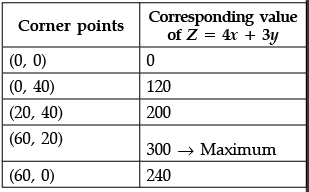
Q.44: The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in Column A and Column B
(a) The quantity in column A is greater.
(b) The quantity in column B is greater.
(c) The two quantities are equal.
(d) The relationship cannot be determined on the basis of the information supplied.
Correct Answer is Option (b)
Q.45: Is the value of the determinant 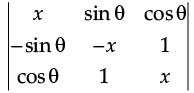 dependent on the value of q.
dependent on the value of q.
(a) Yes
(b) No
(c) None of the above
(d) All of the above
Correct Answer is Option (b)
The determinant comes out to be –x3 after calculation which is independent of θ.
CASE-STUDY
Neha wants to prepare a handmade gift box for her sister's birthday at home. For making lower part of box; the takes a square piece of card board of side 10 cm.
Based on the given information, answer the following questions.
Q.46: If x cm be the length of the square card board which is to be cut off from corners of the square piece of side 10 cm, the possible value of x will be given by the interval.
(a) [0, 10]
(b) (0, 20)
(c) (0, 5)
(d) None of these
Correct Answer is Option (c)
Since, side of square is of length 10 cm therefore x ∈ (0, 5)
Q.47: Volume of the open box formed by folding up the cutting corner can be expressed as
(a) V = x(10 – 2x)2
(b) V = (x – 10)(10 – 2x)2
(c) V = x(10 – 2x)(10 + 2x)
(d) V = (x – 5)(10 – 2x)2
Correct Answer is Option (a)
Height of open box = x cm
Length of open box = 10 – 2x
and width of open box = 10 – 2x
∴ Volume of the open box
= x(10 – 2x)(10 – 2x)
= x(10 – 2x)2
Q.48: The values of x for which dV/dx = 0 are,
(a) 5/3, - 2
(b) 5, 5/3
(c) 5-, 3/2
(d) 5, 3
Correct Answer is Option (b)
V = x(10 – 2x)2
+ (10 – 2x)2
= (10 – 2x)[–4x + 10 – 2x]
= (10 – 2x)(10 – 6x)
Now dV/dx = 0⇒ 10 – 2x = 0 or 10 – 6x = 0
⇒ x = 5 or 5/3.
Q.49: Neha is intrested in maximising the volume of the box. So, what should be the side of the square to be cut off so that the volume of the box is maximum.
(a) 4 cm
(b) 3 cm
(c) 5 cm
(d) 5/3 cm
Correct Answer is Option (d)
∴ Volume of the box will be maximum
When x = 5/3 cm.
Q.50: The maximum volume of the box is
(a) 1000/9 cm3
(b) 2000/9 cm3
(c) 2000/27 cm3
(d) 1000/27 cm3
Correct Answer is Option (c)
V = x(10 – 2x)2∴ Maximum volume
|
203 videos|377 docs|167 tests
|