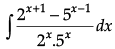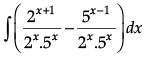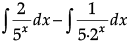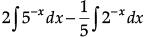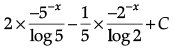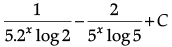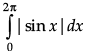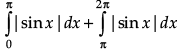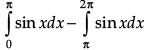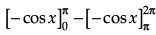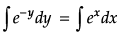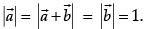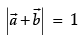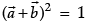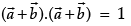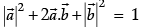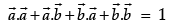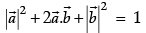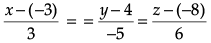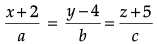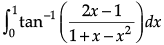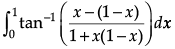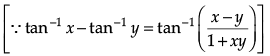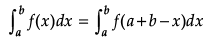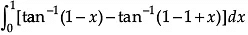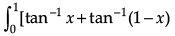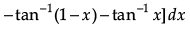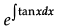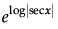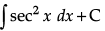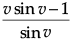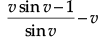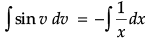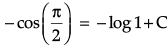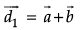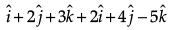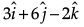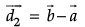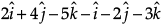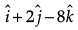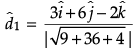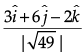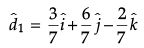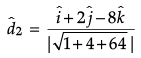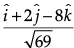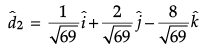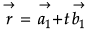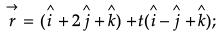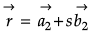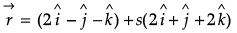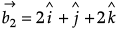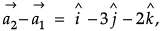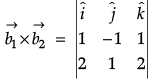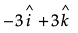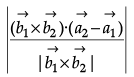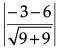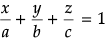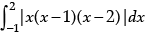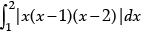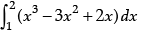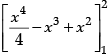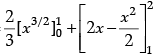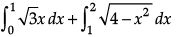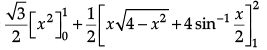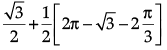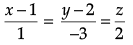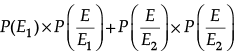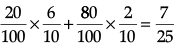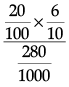Class 12 Mathematics: CBSE Sample Question Paper- Term II (2021-22)- 3 | Sample Papers for Class 12 Medical and Non-Medical PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 120 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 120 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three sections A, B and C. Each part is compulsory.
- Section - A has 6 short answer type (SA1) questions of 2 marks each.
- Section - B has 4 short answer type (SA2) questions of 3 marks each.
- Section - C has 4 long answer type questions (LA) of 4 marks each.
- There is an internal choice in some of the questions.
- Q14 is a case-based problem having 2 sub parts of 2 marks each.
Section - A
Q.1. Find 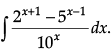
OR
Evaluate 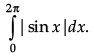
=
=
=
=
=
=
OR
Let I =
=
=
=
= [-cosπ + cos0] - [-cos2π + cosπ]
= [1 + 1] - [ -1 - 1]
= 2 + 2
= 4
Q.2. Find the general solution of the differential equation  .
.
dy/dx = ex+y
= ex . ey
⇒ dy/ey = exdx
⇒ e-ydy= exdx
Integrating both sides, we get:
⇒ -e-y = ex + k
⇒ ex + e-y = -k
⇒ ex + e-y = C (where, C= -) 1
Q.3. Let 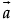 and
and 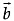 be two-unit vectors and q be the angle between them. Then for what value of θ,
be two-unit vectors and q be the angle between them. Then for what value of θ, 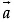 +
+ 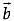 is a unit vector.
is a unit vector.
Let
and
be two-unit vectors and q be the angle between them.
Then,
Now ,and
is a unit vector then
⇒
⇒
⇒
⇒
⇒
⇒
⇒ cosθ = -1/2
⇒ θ = 2π/3
So that,is a unit vector if θ = 2π/3
Q.4. Find the cartesian equation of the line which passes through the point (– 2, 4, – 5) and is parallel to the line 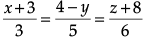 .
.
Given line
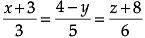
[If two lines are parallel, then they both have proportional direction ratio]
or
Here, given point is (– 2, 4, – 5) with D.R’s. 3, – 5, 6
Therefore, cartesian equation of parallel line will be :
or
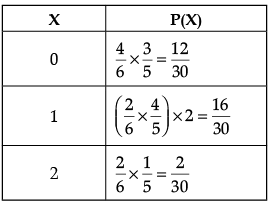
Q.5. A refrigerator box contains 2 milk chocolates and 4 dark chocolates. Two chocolates are drawn at random. Find the probability distribution of the number of milk chocolates. What is the most likely outcome?
Let X denote the number of milk chocolates drawn
Most likely outcome is getting one chocolate of each type.
Q.6. If P(not A) = 0.7, P(B) = 0.7 and P(B/A) = 0.5, then find P(A/B).
= 0.7 ⇒ 1 -P(A)=0.7 ⇒ P(A)=0.3
P(A∩B) = P(A)P(B/A) = 0.3 x 0.5 = 0.15= 0.15/0.7 = 15/70 or 3/14
Section - B
Q.7. Find the value of 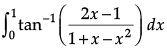
Let
I =
⇒ I =
⇒ I =...(i)
Apply,
⇒ I =
⇒ I =..(ii)
Adding equations (i) and (ii), we obtain
2I =
⇒ 2I= 0
⇒ I= 0
Q.8. Find the general solution of dy/dx + ytan x = sec x.
OR
Solve the differential equation: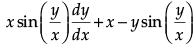 = 0
= 0
Given that x = 1 when y = π/2.
Given differential equation is
dy/dx + ytan x = sec x
which is a linear differential equation
Here, P = tan x, Q = sec x,
∴ IF =
=
= sec x
The general solution is
y . sec x =
⇒ y . sec x =
⇒ y . sec x = tanx + C
OR
We have,= 0
⇒ dy/dx =...(i)
Above differential equation is a homogeneous equation
Put y = vx
Then, dy/dx = v + xdv/dx ...(ii)
From (i) and (ii),
⇒ v + xdv/dx =
⇒ v + xdv/dx =
⇒ v + xdv/dx =
⇒ xdv/dx =
⇒ xdv/dx =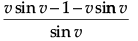
⇒ xdv/dx = -1/sin v
⇒ sin vdv = -1/xdx [Here x ≠ 0]
Now, integrating both sides
⇒
⇒ -cos v = -log |x| + C
Put, v = y/x0
⇒= -log |x| + C ...(iii)
Also, given that x = 1, when y = π/2
⇒
C= 0
⇒
Therefore log |x| = cos(y/x) is the required solution.
Q.9. If 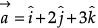 and
and 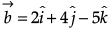 represent two adjacent sides of a parallelogram, find unit vectors parallel to the diagonals of the parallelogram.
represent two adjacent sides of a parallelogram, find unit vectors parallel to the diagonals of the parallelogram.
Given that,
and
are two adjacent sides of a parallelogram.
Let us supposeand
are two diagonals of parallelogram.
Then,
=
=
and
=
=
Now, unit vector parallel to,
=
And unit vector parallel to,
=
Q.10. Find the shortest distance between the lines:
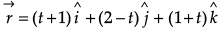
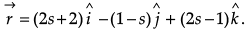
OR
A plane meets the co-ordinate axes at A, B and C such that the centroid of ΔABC is the point (α, β, γ). Show that the equation of the plane is x/α + y/β + z/γ = 3.
Equations of lines can be written as :
⇒
⇒
Here,and
Then,
and,
=
∴ Shortest distance
=
=
= 3/√2 or 3√2/2 units
OR
Since, the equation of the plane having intercept a, b and c on the three co-ordinate axes is:
Here, the co-ordinates of A, B and C are (a, 0, 0), (0, b, 0) and (0, 0, c) respectively.
The centroid of ΔABC is.
Equatingto (α, β, γ) we get a = 3α, b = 3β and c = 3γ
Thus, the equation of the plane is= 1
or x/α + y/β + z/γ = 3
Section - C
Q.11. Evaluate : 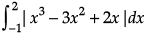 .
.
The given definite integral
=
=+
=-
=-
= 9/4 + 1/4 + 1/4 = 11/4
Q.12. Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and x-axis.
OR
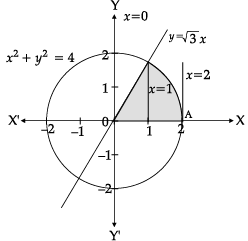
Using integration, find the area of the region
{(x, y) : 0 ≤ y ≤ √3x, x2 + y2 ≤ 4}
Solving x + y = 2 and y2 = x simultaneously, we get the points of intersection as (1, 1) and (4, – 2).
The required area = The shaded area
=
=
= 2/3 + 1/2 = 7/6 square units
OR
Solving y = √3x and x2 + y2 = 4, we get the points of intersection as (1, √3 )and ( -1, -√3 )
The required area = The shaded area
=
=
=
= 2π/3 square units
Q.13. Find the foot of the perpendicular from the point (1, 2, 0) upon the plane x – 3y + 2z = 9. Hence, find the distance of the point (1, 2, 0) from the given plane.
The equation of the line perpendicular to the plane and passing through the point (1, 2, 0) is
The coordinates of the foot of the perpendicular are (μ + 1, –3μ + 2, 2μ) for some μ
These coordinates will satisfy the equation of the plane. Hence, we have
μ + 1 -3(–3μ + 2) + 2(2μ)= 9⇒ μ = 1
The foot of the perpendicular is (2, –1, 2). 1 Hence, the required distance
=
= √14 units
Case-Based/Data Base
Q.14. An insurance company believes that people can be divided into two classes: those who are accident prone and those who are not. The company's statistics show that an accident-prone person will have an accident at sometime within a fixed one-year period with probability 0.6, whereas this probability is 0.2 for a person who is not accident prone. The company knows that 20 percent of the people is accident prone.
The company's statistics show that an accident-prone person will have an accident at sometime within a fixed one-year period with probability 0.6, whereas this probability is 0.2 for a person who is not accident prone. The company knows that 20 percent of the people is accident prone. Based on the given information, answer the following questions.
(i) What is the probability that a new policyholder will have an accident within a year of purchasing a policy?
(ii) Suppose that a new policyholder has an accident within a year of purchasing a policy. What is the probability that he or she is accident prone?
Let E1 =The policy holder is accident prone.
E2 = The policy holder is not accident prone.
E = The new policy holder has an accident within a year of purchasing a policy.
(i) P(E) =
=
(ii) By Bayes' Theorem,
=
= 3/7
|
159 docs|4 tests
|