Class 8 Maths Chapter 3 HOTS Questions - Understanding Quadrilaterals
Q1: In Fig. ABCD and AEFG are two parallelograms. If ∠C=55o, determine ∠F.
(A) 27.5o
(B) 45o
(C) 55o
(D) 65o
Ans: c
Sol: ABCD and AEFG are two parallelograms sharing two sides AD (or AG) and AE (or AE) and the included angle.
∠C=55o.
To find out- ∠F
We have ∠F=∠A ......(opposite angles of a parallelogram).........(i)
Again ∠A=∠C ......(opposite angles of a parallelogram)...........(ii)
∴∠F=∠C ......[From (i) and (ii)]
And ∠C=55o .......(given)
⇒∠F=55o
Q2: Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 6 cm
Ans: b
Sol: Let ABCD be a quadrilateral.
Given, opposite angles of a quadrilateral ABCD are equal.
So, opposite sides of the quadrilateral ABCD are equal.
⇒AB = CD
Given, AB = 4 cm
Therefore, CD = 4 cm.
Q3: Which of the following is not always true for a parallelogram?
(a) Opposite sides are equal.
(b) Opposite angles are equal.
(c) Opposite angles are bisected by the diagonals.
(d) Diagonals bisect each other.
Ans: c
Sol: Opposite angles are bisected by the diagonals.
The above statement is not true for every parallelogram.
It is true only for a rhombus (diamond) or square where the diagonals bisect the opposite angles they connect, and diagonals are perpendicular.
In rectangles, the diagonals do not bisect the angles and are not perpendicular, but they do bisect each other.
Q4: All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
(a) Rectangle
(b) Trapezium
(c) Rhombus
(d) Parallelogram
Ans: a
Sol: We know that the sum of the angles of the quadrilateral is 360o
Now, the quadrilateral in given question has all angles equal.
∴ Each angle =360o ÷ 4 = 90o
So, this quadrilateral would be rectangle or a square.
Q5: In the above figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD=CD? Why or why not?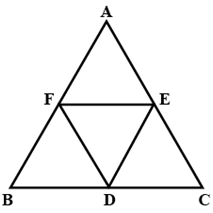
(a) Yes
(b) No
(c) May be
(d) Cannot be determined
Ans: a
Sol: Given:
ABC is a triangle. D,EF are points on BC,CA.AB taken in order. BDEF anf FDCE are parallelograms.
To Prove:
BD=CD
Proof:
In parallelogram BDEF,
BD=EF…(i) [Opposite sides of a parallelogram are equal.]
In parallelogram FDCE,
CD=EF…(ii) [Opposite sides of a parallelogram are equal.]
From (i) and (ii),
BD=CD
Hence, proved.
Q6: Given a parallelogram ABCD, if ∠A=60∘ then ∠D is equal to:
(a)110∘
(b)140∘
(c)120∘
(d)130∘
Ans: c
Sol: ∠A = 60∘, therefore the opposite angle C=60∘
∠B = ∠D [Rule of parallelogram] as they are opposite angles.
Let ∠B and ∠D be x
⇒ x + x + ∠A +∠B = 360∘ [ sum of all sides of a polygon ]
⇒2x + 60∘+ 60∘ =360∘
⇒ 2x = 240∘
⇒ x = 120∘
∴ ∠D = 120∘
Hence, the answer is 120∘.
Q7: Two consecutive angles of a parallelogram are in the ratio 1 : 3, then the smaller angle is:
(a) 50∘
(b) 90∘
(c) 60∘
(d) 45∘
Ans: d
Sol: Step -1: Formulating the sum of angles
We know that, sum of two consecutive angles of a parallelogram = 180∘
Given angles are in the ratio 1 : 3
∴The angles are x and 3x.
∴ x + 3x = 180∘
⇒ 4x = 180∘
⇒ x = 180/4
∴ x = 45∘
∴The smaller angle is 45∘
Hence, The smaller angle is 45∘. Hence, option D is correct.
Q9: In figure, ABCD is a parallelogram. If ∠DAB=60∘ and ∠DBC=80∘, ∠CDB is: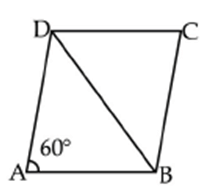
(a) 40∘
(b) 80∘
(c) 60∘
(d) 20∘
Ans: a
Sol: Given ABCD is a parallelogram and BD is the diagonal.
AB∥CD
⇒ ∠CBD = ∠ADB = 80∘
We have ∠DAB = ∠BCD = 60∘
Diagonal BD forms a triangle CBD,
⇒ ∠DCB+∠CBD+∠CDB = 180∘ [Sum of ∠ les of a triangle]
⇒ 60∘ + 80∘ +∠CDB=180∘
∴ ∠CBD = 40∘, ∠ADB = 80∘
Hence, the answer is 40∘.
Q10: In figure, PQRS is a parallelogram in which ∠PSR = 125∘, ∠RQT is equal to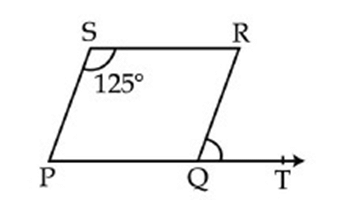
(A) 75∘
(B) 65∘
(C) 55∘
(D) 125∘
Ans: c
Sol: Given PQRS is a parallelogram.
⇒ ∠PSR = ∠PQR = 125° [ i.e, opposite angles ]
∴ ∠RQT = 180°−125°
=55°.
Hence, the answer is 55°.
Q11: In a parallelogram ABCD, if AB = 2x + 5, CD = y + 1, AD = y + 5 and BC = 3x − 4, what is the ratio of AB and BC?
(a) 71 : 21
(b) 12 : 11
(c) 31 : 35
(d) 4 : 7
Ans: c
Sol: In parallelogram, opposite sides are parallel and equal
∴ AB = CD and AD = BC
⇒ 2x + 5 = y + 1⟶1
⇒ 3x − 4 = y + 5 ⟶2
Equation 2-equation 1
(3x − 2x) −4 − 5 = 0 + 4
x = 13
Put value of x in 1
2(13) + 5 − 1 = y
y = 30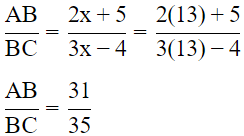
∴ AB : BC = 31 : 35
Q12: A school was having 4 Hexagonal buildings joined to each other. They wanted to utilize the space between the 4 buildings to make a playground. The shape is that of a parallelogram. Can you find the measure of the angles as opposite angles are equal?
(a) 60∘,120∘
(b) 20∘,60∘
(c) 80∘,120∘
(d) 40∘,40∘
Ans: a
Sol: x and y are exterior angles of the regular polygon.
360/6 = 60 i.e value of x angle
Opposite angles are 60∘ +60∘
360∘ − 120∘(60∘ + 60∘)
360∘ = 60∘ + 60∘ + y + y
2y = 360∘ −120∘
y = 240∘/2
y=120∘
Therefore, option A is the correct answer.
Q13: In the given figure, ABCD and BDCE are parallelograms with common base DC . If BC ⊥ BD, then ∠BEC =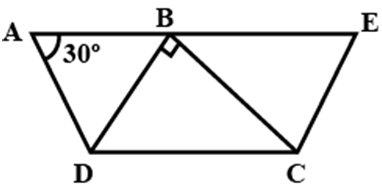
(a) 60∘
(b) 30∘
(c) 150∘
(d) 120∘
Ans: a
Sol: ∠BAD=30∘
∠BCD=30∘ [Opposite angles of parallelogram equal]
Now, in ΔCBD,
∠DBC+∠BCD+∠CDB=180∘
⇒90∘+30∘+∠CDB=180∘
⇒ CDB = 60∘
∴ ∠BEC=60∘ [Opposite angles are equal]
Q14: How many sides does a polygon have if the sum of the interior angles is 8 right angles
Ans: We know that a right angle is of 90∘.
Now, since sum of the interior angles is 8 right angles, therefore, (2n–4)90∘ = 8 × 90∘
2n – 4 = 720/90
⇒ 2n – 4 = 8
⇒ 2n = 8 + 4
⇒ 2n = 12
⇒ n = 12/2 = 6
Hence, the polygon has 6 sides.
Q15: How many sides does a polygon have if the sum of the interior angles is 7 straight angles
Ans: We know that a straight angle is of 180∘.
Now, since sum of the interior angles is 7 straight angles, therefore, (2n – 4)90∘ = 7 × 180∘
2n – 4 = 1260/90
⇒ 2n – 4 = 14
⇒ 2n = 14 + 4
⇒2n = 18
⇒ n = 18/2 = 9
Hence, the polygon has 9 sides.
Q16: How many sides does a polygon have if the sum of the interior angles is 1440∘
Ans: Since sum of the interior angles is 1440∘, therefore, (2n–4)90∘ =1440∘
2n – 4 = 1440/90
⇒ 2n – 4 = 16
⇒ 2n = 16 + 4
⇒ 2n = 20
⇒ n = 20/2 = 10
Hence, the polygon has 10 sides.
Q17: If D,E,F are midpoints of AB,BC,AC respectively prove that BDEF is a ∣∣ gm
Ans: In △ABC, D, E and F are midpoints of BC, AC and AB respectively.
∵ E and F are mid point of AC and AB respectively
∴ FE ∣∣ BC ⇒ FE ∣∣ BD −−−(1)
Similarly DE+ +AB ⇒ DE ∣∣ FB −−−−−(2)
Now, from (1) and (2),
opposite pairs are parallel
∴ BDEF is a parallelogram -----proved.
Q18: In the given figure, ABCD is a trapezium, Diagonals AC and BD interset at Q Prove that the area of ΔAOD is the same as ΔBOC
Ans: Given a trapezium ABCD where AB∥DC ξ diagonal AC ξ BD intersect each other at 0.
We have prove that ar(AOD)=ar(BOC)
Consider △ADC ξ △BDC, ;ie on the same base DC and between the same parallel AB and CD.
∴ Area (△ADC) = Area(△BDC) [Triangle with same base and between the same parallel are equal in area.]
⇒ ar(ADC) − ar(DOC) = ar(BDC) − ar(DOC)
ar(AOD) = ar(BOC)
Hence, the answer is proved.
Q19: ABCD is a parallelogram. The circle through A,B and C intersects CD produced at E. If AB = 10 cm, BC = 8 cm, CE = 14 cm. Find AE
Ans: ABCD is a parallelogram and a circle is drawn through A, B and C which intersects CD produced, at E
AB = 10cm BC = 8cm CE = 14cm
Now,
∠AED + ∠ABC = 180∘ →(1) (Sum of opposite angles of a cyclic quadrilateral is supplementary)
∠EDA+∠ADC=180∘ →(2) (linear pair)
∠EDA+∠ABC=180∘ →(3) (∵ ∠ADC=∠ABC as they are the opposite angles of a parallelogram)
From (1) & (3) we have,
∠AED = ∠EDA→(4)
⇒ in ΔAED two angles are equal, hence the opposite sides corresponding to these angles must also be equal i.e. AE = AD
and AD = BC (opposite sides of a parallelogram are equal)
∴ AE = 8 cm.
Q20: If the adjacent sides of a parallelogram are in the ratio 2 : 3 and the sum of all the sides is 50 cm, find the measure of the sides of the parallelogram.
Ans: The opposite sides of a parallelogram are equal.
Let one of the sides be a and adjacent side be b.
Given:
2a+2b=50
⇒ a + b = 25 ......(1)
Also a : b = 2 : 3 ......(2)
Substituting (3) in (1) we get
2b/3 + b = 25
5b/3 = 25
b=15 cm
∴ a=10 cm …(3)
∴ if ABCD is the parallelogram, then the length of the sides of the parallelogram are:
AB = CD = 10 cm
BC = AD = 15 cm
Hence, solved.
|
94 videos|549 docs|42 tests
|
















