Q1: Give a reason to show that the number given below is a perfect square: 5963
Sol: The unit digit of the square numbers will be 0, 1, 4, 5, 6, or 9 if we examine the squares of numbers from 1 to 10. Thus, the unit digit for all perfect squares will be 0, 1, 4, 5, 6, or 9, and none of the square numbers will end in 2, 3, 7, or 8.
Given 5963
We have the property of a perfect square, i.e. a number ending in 3 is never a perfect square.
Therefore the given number 5963 is not a perfect square.
Q2: 2025 plants are to be planted in a garden in a way that each of the rows contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Sol:
Let the number of rows be x.
Thus, the number of plants in each row = x.
Total many contributed by all the students = x × x = x²
Given, x² = Rs.2025
x2 = 3 × 3 × 3 × 3 × 5 × 5
⇒ x2 = (3 × 3) × (3 × 3) × (5 × 5)
⇒ x2 = (3 × 3 × 5) × (3 × 3 × 5)
⇒ x2 = 45 × 45
⇒ x = √(45 × 45)
⇒ x = 45
Therefore,
Number of rows = 45
Number of plants in each row = 45
Q3: Write a Pythagorean triplet whose one member is:
(i) 6
(ii) 14
(iii) 16
(iv) 18
Sol: Any natural number m, 2m, m2–1, m2+1 is a Pythagorean triplet.
(i) 2m = 6
m = 6/2
m = 3
m²–1= 3² – 1 = 9–1 = 8
m²+1= 3²+1 = 9+1 = 10
Thus, (6, 8, 10) is a Pythagorean triplet.
(ii) 2m = 14
⇒ m = 14/2 = 7
m²–1= 7²–1 = 49–1 = 48
m²+1 = 7²+1 = 49+1 = 50
Thus, (14, 48, 50) is not a Pythagorean triplet.
(iii) 2m = 16
⇒ m = 16/2 = 8
m²–1 = 8²–1 = 64–1 = 63
m²+ 1 = 8²+1 = 64+1 = 65
Thus, (16, 63, 65) is a Pythagorean triplet.
(iv) 2m = 18
⇒ m = 18/2 = 9
m²–1 = 9²–1 = 81–1 = 80
m²+1 = 9²+1 = 81+1 = 82
Thus, (18, 80, 82) is a Pythagorean triplet.
Q4: By what least number should the number be divided to obtain a number with a perfect square? In this, in each case, find the number whose square is the new number 4851.
Sol: The number is a perfect square if and only if the prime factorization creates pairs; it is not exactly a perfect square if it is not paired up.
Given 4851,
Resolving 4851 into prime factors, we obtain
4851 = 3 X 3 X 7 X 7 X 11
= (32 X 72 X 11)
To obtain a perfect square, we need to divide the above equation by 11
we obtain, 9075 = 3 X 3 X 7 X 7
The new number = (9 X 49)
= (3² X 7² )
Taking squares on both sides of the above equation, we obtain
∴ The new number = (3 X 7)²
= (21)²
Therefore, the new number is a square of 21
Q5: Without adding, find the sum of the following:
(1+3+5+7+9+11+13+15+17+19+21+23)
Sol: (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23)
As per the given property of perfect square, for any natural number n, we have some of the first n odd natural numbers = n²
But here n = 12
By applying the above the law, we get
thus, (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23)
= 12²
= 144
Q6: By what least number should the given number be divided to get a perfect square number? In each of the following cases, find the number whose square is the new number 1575.
Sol: A method for determining the prime factors of a given number, such as a composite number, is known as prime factorisation.
Given 1575,
Resolve 1575 into prime factors, we get
1575 = 3 X 3 X 5 X 5 X 7 = (3² X 5² X 7)
To obtain a perfect square, we have to divide the above equation by 7
Then we get, 3380 = 3 X 3 X 5 X 5
New number = (9 X 25) = (3² X 5² )
Taking squares on both sides of the above equation, we get
∴ New number = (3 X 5)² = (15)²
Therefore, the new number is a square of 15.
Q7:If m is the required square of a natural number given by n, then n is
(a) the square of m
(b) greater than m
(c) equal to m
(d) √m
Ans: (d)
Sol: n² = m
Then,
= n = √m
Q8: The sides of a right triangle whose hypotenuse is 17cm are _________ and _________.
Sol:
For each natural number, m > 1, 2m , m2 –1 and m2 + 1 form a Pythagorean triplet.
Now,
m² + 1 = (2m)² + (m2 – 1)²
Where,
m² + 1 = 17
m² = 17 – 1
m² = 16
m = √16
m = 4
Then,
2m = 2 × 4
= 8
And,
m² – 1 = 4² – 1
= 16 -1
= 15
Q9: Use the following identity and find the square of 189.
(a – b)² = a² – 2ab + b²
Sol: 189 = (200 – 11) 2
= 40000 – 2 x 200 x 11 + 112
= 40000 – 4400 + 121
= 35721
Q10: What would be the square root of the number 625 using the identity
(a +b)² = a² + b² + 2ab?
Sol: (625)²
= (600 + 25)²
= 600² + 2 x 600 x 25 +25²
= 360000 + 30000 + 625
= 390625
Q11:Show that the sum of two consecutive natural numbers is 13².
Sol: Let 2n + 1 = 13
So, n = 6
So, ( 2n + 1)² = 4n² + 4n + 1
= (2n² + 2n) + (2n² + 2n + 1)
Substitute n = 6,
(13)² = ( 2 x 6² + 2 x 6) + (2 x 6² + 2 x 6 + 1)
= (72 + 12) + (72 + 12 + 1)
= 84 + 85
Q12: Find the smallest whole number from which 1008 should be multiplied to obtain a perfect square number. Also, find out the square root of the square number so obtained.
Sol:
Let us factorise the number 1008.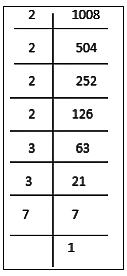
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
= ( 2 × 2 ) × ( 2 × 2 ) × ( 3 × 3 ) × 7
Here, 7 cannot be paired.
Therefore, we will multiply 1008 by 7 to get a perfect square.
New number so obtained = 1008 ×7 = 7056
Now, let us find the square root of 70567056 = 2 × 2 × 2 × 2 × 3 × 3× 7 × 7
7056 = (2 × 2 ) × ( 2 × 2 ) × ( 3 × 3 ) ×( 7 × 7 )
7056 = 2² × 2² × 3² × 7²
7056 = (2 × 2 × 3 × 7)²
Therefore;
√7056 = 2 × 2 × 3 × 7
= 84
Q13: √(1.96) = _________.
Sol: We have,
= √(1.96)
= √(196/100)
= √((14 × 14)/(10 × 10))
= √(142 / 102)
= 14/10
= 1.4
Q14: There are _________ perfect squares between 1 and 100.
Sol: There are 8 perfect squares between 1 and 100.
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16
5 × 5 = 25
6 × 6 = 36
7 × 7 = 49
8 × 8 = 64
9 × 9 = 81
Q15: Show that each of the numbers is a perfect square. In each case, find the number whose square is the given number:
7056
Sol: 7056,
A perfect square is always expressed as a product of pairs of prime factors.
Resolving 7056 into prime factors, we obtain
7056 = 11 X 539
= 12 X 588
= 12 X 7 X 84
= 84 X 84
= (84)²
Thus, 84 is the number whose square is 5929
Therefore,7056 is a perfect square.
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7 
7056 = 2 × 2 × 2 × 2 × 3 × 3× 7 × 7
