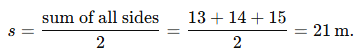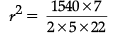Class 9 Math: Sample Question Paper Term II- 2 (With Solutions) | Mathematics (Maths) Class 9 PDF Download

Class IX Mathematics

Max. Marks: 40

General Instructions :

1. The question paper consists of 14 questions divided into 3 sections A, B and C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Q.1: Find the value of the polynomial
p(x) = x³ – 3x² – 2x + 6 at x = √2

Given,  p(x) = x³ – 3x² – 2x + 6
Then, p(√2) = (√2)³ - 3(√2)² - 2(√2) + 6
= 2√2 - 6 - 2√2 + 6

= 0

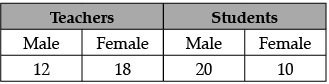
Q.2: Teachers and students are selected at random to make two teams of 30 members each on sports day to participate in the event of "tug of war". The number of volunteers are as follows: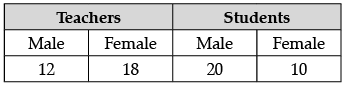

Find the probability that the person chosen at random
(i) is a male
(ii) is a female student. 

OR

In a one-day cricket Match, Sachin played 40 balls and hit 12 sixes and Saurav played 30 balls and hit 9 fours. Find the probability that Sachin will hit a six in the next ball and also find the probability that Saurav will not hit a four in the next ball.

Let E₁ and E₂ be the events of a male (Teachers and students) and a female students.

Total number of volunteers i.e., n(S)
= 12 + 18 + 20 + 10 = 60
 (i) Total number of males i.e., n(E₁)
= 12 + 20 = 32
P(volunteer is male) = n(E₁)/n(S) = 32/60 = 8/15
(ii) P(volunteer is female student)
n(E₂)/n(S) = 10/60 = 1/6

OR

Total number of balls faced by Sachin = 40
Number of balls on which he hit a six = 12
Let E1 be the event of hitting a six.
∴ Number of outcomes = 12
∴ P(E₁) = 12/40 = 3/10 = 0.3
Now, Total number of balls faced by Saurav = 30
Let E₂ be the event of Saurav did not hit a four Number of outcomes = 30 – 9 = 21
P(E₂) = 21/30= 7/10 = 0.7

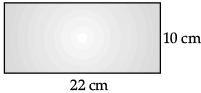
Q.3: A rectangular piece of paper is 22 cm long and 10 cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.

According to question,
2πr = 22 (Circumference of cylinder)
2 x 22/7 x r = 22
r = 7/2
Volume of the cylinder = πr²h
= 22/7 x 7/2  x 7/2 x 10
∴ Volume of the cylinder =  385 cm³

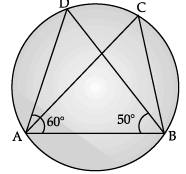
Q.4: In the figure, if ∠DAB = 60°, ∠ABD = 50°, then find ∠ACB.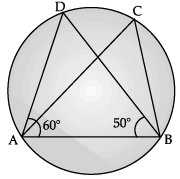

OR

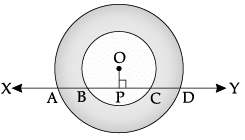
If a line intersects two concentric circles with common centre O, at A, B, C and D. Prove that AB = CD.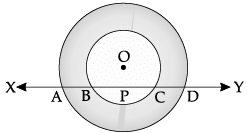

In ΔADB,
By angle sum property
∠ABD + ∠ADB + ∠BAD = 180°

∴ 50° + ∠ADB + 60° = 180°
∴ ∠ADB = 180° – (50° + 60°)
∴ ∠ACB = ∠ADB = 70°. [∵ angles in the same segment of a circle are equal]
hence, ∠ ACB = 70°

OR

Draw OP perpendicular to XY from the centre O to a chord BC and bisecting it.
OP ⊥ to chord BC.
or, BP = PC   ...(i)
Similarly, AP = PD ...(ii)
Subtracting eqn. (i) from eqn. (ii), we get
AP – BP = PD – PC
or, AB = CD Hence Proved.

Q.5: If y = 2 and y = 0 are the zeroes of the polynomial f(y) = 2y³ – 5y² + ay + b, find the value of a and b.

Given, f(y) = 2y³ – 5y² + ay + b
∴ y = 2 is a zero of f(y)
∴ f(2) = 2(2)³ – 5(2)² + a(2) + b = 0
or, 16 – 20 + 2a + b = 0
or, 2a + b = 4
Also, y = 0 is a zero of f(y).
f(0) = b = 0
From (i), 2a + 0 = 4

or, a = 2
∴ a = 2, b = 0

Q.6: A die is rolled 200 times and its outcomes are recorded as below:

Find probability of getting:
(i)  An even prime
(ii) A  multiple of 3.

(i) An even prime number i.e., '2'.
∴ P(getting an even prime number) = 35/200
= 7/40
(ii) Multiple of 3 i.e., 3 and 6
∴ P(getting multiple of 3) = 40+30 / 200 = 70/200
= 7/20

Q.7: If f(x) = 5x² – 4x + 5, find f(1) + f(– 1) + f(0).

Given, f(x) = 5x² – 4x + 5
f(1) = 5 – 4 + 5
= 6
and f(– 1) = 5(– 1)² – 4(– 1) + 5
= 5 + 4 + 5 = 14
and f(0) = 5
∴ f(1) + f(– 1) + f(0) = 6 + 14 + 5 = 25.

Q.8: Construct ∠POY = 30°, using compass and ruler. 

Steps of Construction :
(i) Draw any line OP.

(ii) With O as centre and any suitable radius, draw an arc to meet OP at R.
(iii) With R as centre and same radius (as in step (ii)),draw an arc to intersect the previous arc at S.
(iv) Join OS and produce it to Q, then∠ POQ = 60°.
(v) With R as centre and any suitable radius(>1/2 RS), draw an arc. Also, with S as centre and same radius draw another arc to intersect the previous arc at Y.
(vi)  Join OY. ∠POY is the required angle of 30°.

Q.9: The total surface area of a solid right circular cylinder is 1540 cm². If the height is four times the radius of the base, then find the height of the cylinder.

OR

How much ice-cream can be put into a cone with base radius 3.5 cm and height 12 cm ?

Let the radius and height of the cylinder be r and h respectively, then
T.S.A. of a cylinder = 1540 cm² [given]
∴ 2πr(h + r) = 1540 cm²
Also, h = 4r [given]
∴ 2πr (4r + r) = 1540
or, 2π × 5r² = 1540
or,
or, r² = 49

or, r = 7 cm
Now h = 4r
Hence, height of the cylinder = 28 cm.

OR

Radius (r) = 3.5 cm, height (h) = 12 cm
So, volume of a cone = quantity of ice-cream
∴ Quantity of ice-cream
= 1/3πr²h
= 1/3 x 22/7 x 3.5 x 3.5 x 12
= 154 cm³

Q.10: Construct a ΔPQR in which QR = 6 cm, Ð∠Q = 60° and PR – PQ = 2 cm.

Steps of Construction :
(i) Draw QR  = 6 cm
(ii) Draw ∠Q  = 60°. Let the line be QX.
(iii) With Q  as centre and radius 2 cm, cut an arc on QY, Let the arc intersect QY at S.
(iv) Join R S.
(v) Draw perpendicular bisector AB of RS which intersect QX at point P.
(vi) Join P R.
∴ ΔPQR is required triangle.

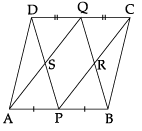
Q.11: In the given figure, ABCD is a parallelogram. P and Q are the mid-points of AB and DC. Show that: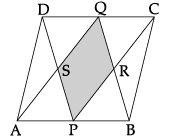

(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.

(i) Since, ABCD is a parallelogram
∴ AB = CD and AB || CD

or, 1/2 AB = 1/2 CD
i.e., AP = CQ and AP || CQ
Hence, A PCQ is a parallelogram.
(ii) Again,
1/2 AB = 1/2 CD [From part (i)]
i.e., PB = DQ and PB || DQ
Hence, D PBQ is a parallelogram. Proved.
(iii) QS || PR and SP || QR
Hence,  PSQR is a parallelogram. Proved.

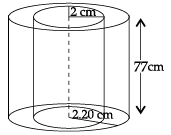
Q.12: A metal pipe is 77 cm long. The inner diameter of a cross-section is 4 cm, the outer diameter being 4.4 cm. Find its:
(i) inner curved surface area
(ii) outer curved surface area
(iii) total surface area. (use π = 22/7)

OR

The frame of a lampshade is cylindrical in shape. It has base diameter 28 cm and height 17 cm. It is to be covered with a decorative cloth. A margin of 2 cm is to be given for folding it over top and bottom of the frame. If 1/12 of cloth is wasted in cutting and pasting, find how much cloth is required to be purchased for covering the frame.

Inner radius (r) = 2 cm
Outer radius (R) = 2.2 cm

Height (h) = 77 cm
(i) C.S.A. (Inner) = 2πrh
= 2 x 22/7 x 2 x 77
= 968 cm²

(ii) C.S.A. (Outer) = 2πRh
= 2 x 22/7 x 2.2 x 77
= 1064.8 cm²
(iii) Area of top= π(R + r)(R – r)
= 22/7 x 4.2 x 0.2
= 2.64 cm²
= Area of the bottom
∴ T.S.A.=Inner (C.S.A.) + Outer (C.S.A.) + Area of top + Area of bottom
= 968 + 1064.8 + 2 × 2.64
= 2038.08 cm².

OR

Base diameter = 28 m
Base radius = 28/2 = 14 cm
Height of cloth required = 17 + 2 + 2
= 21 cm
Area of cloth required = Curved surface area of cylinder of radius 14 cm and height 21 cm
= 2πrh
= 2 x 22/7 x 14 x 21
= 1848 cm²

Let A sq. cm of cloth be purchased.
So, wastage of cloth for cutting and pasting
= A/12 cm²
Area of cloth actually used
=  cm²
Area of cloth actually used = Area of cloth required
or, 11/12A = 1848
or, A = 1848 x12 / 11 =  2016 cm²

Case Study-1
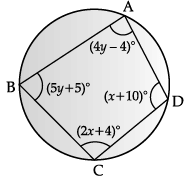
Q.13: Read the following text and answer the questions given below: Four boys are playing with a ball in a circular park. The positions of each boy is represented by A, B, C and D in the following diagram.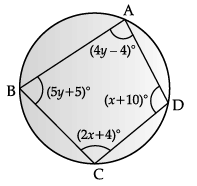

Give answer the following questions:

(i) Find the values of x and y.
(ii) Find ∠A and ÐB. Also prove that ∠A + ∠C = 180°.

(i)
 
Since, the opposite angles of a cyclic quadrilateral are supplementary.
∴ ∠A + ∠C = 180°
⇒ 4y – 4 + 2x + 4 = 180°
⇒ x + 2y = 90°       ...(i)
and ∠B + ∠D = 180°
⇒ 5y + 5 + x + 10 = 180°
⇒ x + 5y = 165°    ...(ii)
On solving, we get x = 40° and y = 25°
(ii) ∠A = 4y – 4 [given]
Putting y = 25 from part (i), we get
∠A = 4 × 25 – 4 = 96°
and ∠B = 5y + 5  [given]
Putting, y = 25, we get
∠B = 5 × 25 + 5 = 130°
Similarly, ∠A = 4y – 4 = 96° [Proved above]
and ∠C = 2x + 4
Putting x = 40 from part (i), we get
∠C = 2 × 40 + 4 = 84°
∠A + ∠C = 96° + 84°
= 180°

Case Study-2
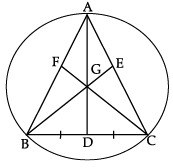
Q.14: Read the following text and answer the following questions on the basis of the same:
A circular park of radius 20 m is situated in a colony. Three boys Anant, Bibhav and Chandra are sitting at equal distances on its boundary, each having a toy telephone in his hands to talk to each other.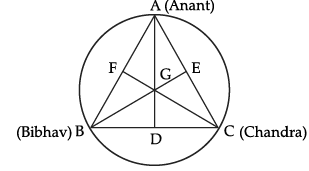

Here, A, B and C be the positions of Anant, Bibhav and Chandra and also let D, E and F are the medians of DABC and G be its centroid.
(i) What is length of GD?
(ii) Find the length of BD.

(i) Since, the centroid of a triangle divides the median in the ratio 2 : 1, then
GA/GD = 2/1
⇒ 20/GD = 2/1
⇒ GD = 10 m

(ii) Here, BG = 20 m [given]
and GD = 10 m [Proved in part (i)]
∴ BD = DC [given]
∠BDG = 90° [∵ G is a centroid]
In right ΔBDG,
(BG)² = (BD)² + (GD)² [Using Pythagoras Theorem]
⇒ (20)² = (BD)² + (10)²
⇒ BD = √ 400 -100
= √300
= 10√3 m.