Class 9 Maths Chapter 4 Practice Question Answers - Linear Equations In Two Variables

Q1: Which of the following equation represents a straight line which is parallel to the x-axis and at a distance 3 units below it?
(a) Any line parallel to x-axis and at a distance of 3 units below it is given by y=9
(b) Any line parallel to x-axis and at a distance of 3 units below it is given by y=−3
(c) Any line parallel to x-axis and at a distance of 3 units below it is given by x=−3
(d) Any line parallel to x-axis and at a distance of 3 units below it is given by x=0
Ans: (b)
Any straight line parallel to x−axis is given by y=k, where k is the distance of the line from x−axis. Here k=−3, because it is below x axis then the equation of the line is y=−3.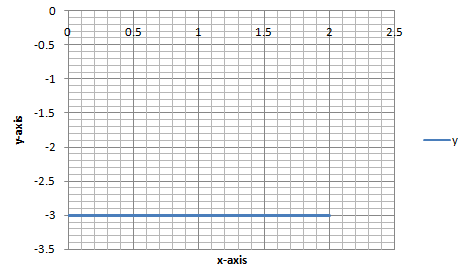

Q2: The equation x=7, in two variables, can be written as
(a) 1.x+1.y=7
(b) 1.x+0.y=7
(c) 0.x+1.y=7
(d) 0.x+0.y=7
Ans: (b)
x =7 can be written as, 1.x+0.y = 7  as the coefficient of x is 1 and that of y is 0.

Q3: Age of x exceeds the age of y by 7yrs. This statement can be expressed as the linear equation as :
(a) x + y + 7 = 0
(b) x − y + 7 = 0
(c) x − y − 7 = 0
(d) x + y − 7 = 0
Ans: (c)
According to question,
x−y=7
⇒ x−y−7=0
So, option C is correct.

Q4: The condition that the equation ax+by+c=0 represent a linear equation in two variables is :
(a) a ≠ 0, b = 0
(b) b ≠ 0, a = 0
(c) a = 0, b = 0
(d) a ≠ 0, b ≠ 0
Ans: (d)
The condition for ax+by+c=0 to be a linear eqaution in two variables is a ≠ 0 , b ≠ 0

Q5: The linear equation x=5 in two variables can be written as :
(a) 1.x+5=10
(b) 0.x+1.y+(−5)=0
(c) 1.x+0.y+(−5)=0
(d) 1.x+1.y+(−5)=0
Ans: (c)
x=5
⇒ x−5=0
⇒ 1.x+(−5)=0
⇒ 1.x+0.y+(−5)=0

Q6: The graph of y=6 is a line
(a) parallel to x−axis & at a distance of 6 units from the x−axis.
(b) parallel to y−axis at a distance of 6 units from the origin.
(c) making an intercept 6 on the x−axis.
(d) making an intercept 6 on both the axes.
Ans: (a)
The given equation is y=6
We can write it as  y=0.x+6
i.e. for every value of x, we have y=6
So, the points are (0,6),(−1,6),(1,6),(3,6)....
On plotting these points, we get a straight line parallel to the x−axis at a distance of 6 units from the x−axis.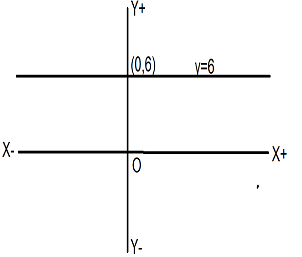

Q7: A class has total 60 students with x girls and y boys. The number of girls is twice the number of boys. Express these statement in the linear equations form.
(a) x + y = 60, x = 2y
(b) x − y = 60, x = 2y
(c) x + y = 60, x = 3y
(d) None of these
Ans: (a)
Given: Total number of students (i.e, boys (y) and girls (x)) in the class is 60.
Therefore,
x+y=60
And number of girls is twice the number of boys, so
x=2y
Hence option A is correct choice

Q8: Write any three linear equations in two variables using the variables x and y?
Ans: We can write many equations which are linear and have the variables x and y.
For example,
x+y=3
x−2y=6
2x+3y=18

Q9: Which of the following represent a line parallel to x-axis?
(a) x+y=3
(b) 2x+3=7
(c) 2−y−3=y+1
(d) x+3=0
Ans: (c)
Any straight line parallel to x−x−axis is given by y=k,y=k, where kk is the distance of the line from x−x−axis.
In option C, we have
2−y−3=y+1
⟹y=−1.

Q10: A bag with total 10 balls contains x blue and y red balls. If the number of blue balls is four times the number of red, then write the two equations.
(a) x+y=10,x=4y
(b) x−y=10,x=4y
(c) xy=10,x+4y=0
(d) None of these
Ans: (a)
Since total number of balls is 10 and only blue (x) and red balls (y) are there in the bag.
⇒x+y=10
and number of blue balls is four time the number of red balls so,
x=4y
Hence option A is correct choice

Q11: Construct 3 equations starting with x = −2.
Ans: x = −2
(1)x = −2
x+2=0
(2)x−2=−2−2
x−2=−4
(3)2x=2×(−2)
2x = −4

Q12: Two candidates A and B contest an election. A gets 46% of the valid votes and is defeated by 1600 votes. Find the total number of valid votes cast in the election ?
Ans: Let total number of vaild votes = x
⇒ votes A got = 46 % of x

= 20000
⇒ Total votes cast = 20000

Q13: What is the sum of 2x − y and 3y − 2x ?
Ans: Sum of 2x−y and 3y−2x
=(2x−y)+(3y−2x)
=2x−y+3y−2x
=2y
Hence, the answer is 2y.

Q14: Express the following linear equation in the form ax+by+c=0 and indicate the values of a,b and c in each case: 2x + 3y = 9.35
Ans: Given :2x + 3y = 9.35
we have to express this in the form of a linear equation of the type,
ax + by + c = 0…(1)
2x + 3y = 9.35
2x + 3y − 9.35 = 0…(2)
Comparing (1)&(2) we get:
Hence, the values of a,b and c are:
a = 2
b = 3
c = −9.35

Q15: Find the solution of given problem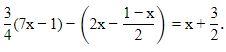
Ans: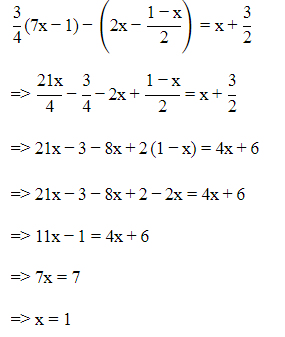


Q16: Express the following linear equation in the form ax+by+c=0 and indicate the values of a,b and c in each case :
5 = 2x
Ans: Given : 5 = 2x
Expressing this in the form of
⇒ ax + by + c = 0
we get 2x + 0.y − 5 = 0
comparing both we get,
⇒ a = 2  b = 0  and  c = −5
Hence, solved.

Q17: Read the following statements carefully and select the correct option.
Statement-I : The graph of the linear equation x + 2y = 6 passes through (8,−1).
Statement II : Every point which satisfies the linear equation is a solution of the equation.
(a) Both Statement-I and Statement-II are true.
(b) Only Statement-I is true.
(c) Only Statement-II is true.
(d) Neither Statement-I nor Statement-II are true.
Ans: (a)
Consider statement I:
Put the given point in equation,
8+2(−1)=8−2=‘6=RHS
Hence given point satisfies the equation of line.
Hence statement I is true
Consider statement II:
Every point lying on the line satisfies the equation of line
As we see from statement I that the point that satisfies the equation of the line is a solution.
Hence statement II is true.

Q18: Solve : 3x=27
Ans: 3x = 27
x = 27/3
x = 9

Q19: Solve : 4x−30=0
Ans: 4x − 30 = 0
4x = 30
x = 30/4
x = 15/2

Q20: Represent 3x − 7 = 0 in the form of ax + by + c = 0 and find the values of a, b and c
Ans: Given 3x−7=0
3x+0y−7=0
ax+y+c=0
Compare to get
a = 3, b = 0 and c = −7