Class 9 Maths - Coordinate Geometry Previous Year Questions
Very Short Answer Type Questions
Q1. A line ∠M is drawn parallel to X-axis at a distance of 5 units from it. On ∠M a point P is marked at a distances of 3 units from the Y-axis. What are the coordinates of P? [2025]
 View Answer
View Answer 
Sol:
The line ∠M can be above or below the x-axis
∴ coordinates of P are (3, 5) or (–3, 5)
Q2. Which of the following statements are true? [2024]
(i) The point (0, –4) lies on y-axis
(ii) The perpendicular distance of the point (5, 7) from the x-axis is 5.
(iii) Point (1, –1) and (–1, 1) lie in the same quadrant.
 View Answer
View Answer 
Sol: Only the statement (i) is true.
Q3. What is the sign of the y-coordinate of a point lying in the III-quadrant? [2023]
 View Answer
View Answer 
Sol: The y-coordinate of a point in III-quadrant is always negative.
Q4. If the two points are A(–2, 7) and B(–3, 4) then what is (abscissa of A) – (abscissa of B)? [2023]
 View Answer
View Answer 
Sol: ∵ abscissa of A = – 2 and abscissa of B = – 3
∵ (– 2) – (– 3) = –2 + 3 =1
Q5. A point (other than zero) is such that [The abscissa of the point] = [The ordinate of the point] In which quadrants can the point lie? [2021]
 View Answer
View Answer 
Sol: ∵ The coordinates have opposite signs in II and IV quadrants.
∴ the given point lies in I or III quadrant.
Q6. A line ∠M is drawn parallel to X-axis at a distance of 5 units from it. On ∠M a point P is marked at a distances of 3 units from the Y-axis. What are the coordinates of P? [2020]
 View Answer
View Answer 
Sol: The line ∠M can be above or below the x-axis
∴ coordinates of P are (3, 5) or (–3, 5)
Short Answer Type Questions
Q1. Look at the following figure and answer the following: [2025](i) What is the abscissa of P?
(ii) What is the ordinate of Q?
(iii) What is the ordinate of R?
(iv) What is the abscissa of S?
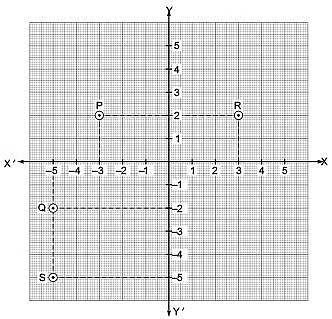
 View Answer
View Answer 
Sol: (i) The abscissa of P is –3.
(ii) The ordinate of Q is –2.
(iii) The ordinate of R is 2.
(iv) The abscissa of S is –5.
Q2. Look at the following figure and answer the following: [2024]
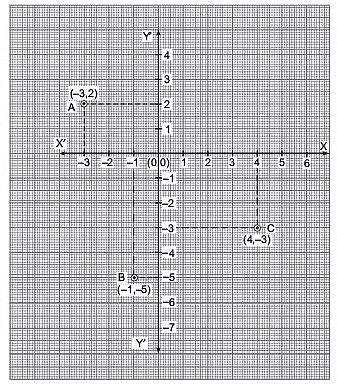
(i) Which point is having its ordinate as (–5)?
(ii) Which point is having abscissa as 4?
(iii) What are the coordinates of origin?
(iv) Which point is having abscissa as (–3)?
 View Answer
View Answer 
Sol: (i) The point B is having its ordinate as (–5).
(ii) The point C is having its abscissa as 4.
(iii) The coordinates of O are (0, 0).
(iv) The point A is having abscissa as (–3).
Q3. Look at the following figure and answer the following: [2023]
(i) Which two points have the same abscissa?
(ii) Which two points have the same ordinate?
 View Answer
View Answer 
Sol:
(i) ∵ The abscissa of the point Q is 6.
The abscissa of the point R is 6.
∴The points Q and R have the same abscissa.
(ii) ∵ The ordinate of P is (–3).
The ordinate of R is (–3).
∴ The points P and R have the same ordinate.
Q4. Read the coordinates of the vertices of the triangle ABC in the following figure: [2021]
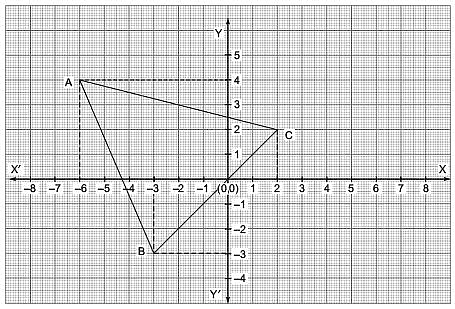
 View Answer
View Answer 
Sol:
The vertices of the triangle are A, B and C.
The coordinates of A are (–6, 4).
The coordinates of B are (–3, –3).
The coordinates of C are (2, 2).
Q5. Write the coordinates of quadrilateral PQRS as shown in the following figure: [2020]
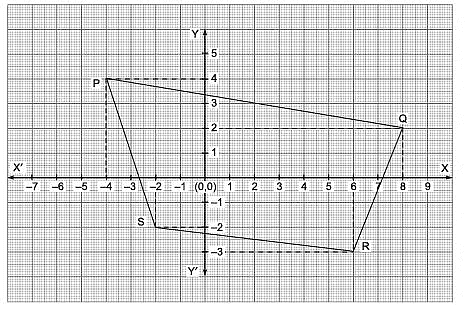
 View Answer
View Answer 
Sol:
The vertices of the quadrilateral are P, Q, R and S.
The coordinates of P are (–4, 4).
The coordinates of Q are (8, 2).
The coordinates of R are (6, –3).
The coordinates of S are (–2, –2).
Long Answer Type Questions
Q1: If two vertices of an equilateral triangle are (3, 0) and (6, 0), find the third vertex. [2025]
 View Answer
View Answer 
Sol:
Let A (3,0), B (6, 0), C (x, y).
∴ ∆ABC is an equilateral
∴ AB = BC = AC
AB2 = BC2 = AC2 …[Squaring throughout
(6 – 3)2 + (0 – 0)2 = (x – 6)2 + (1 – 0)2 = (x – 3)2 + (y – 0)2
9 = x2 – 12x + 36 + y2 = x2 – 6x + 9 + y2

Q2: If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p. [2023]
 View Answer
View Answer 
Sol:
Area of ∆ = 15 sq. units
12 [1(p – 7) + 4(7 + 3)) + (-9)(-3 – p)] = ±15
p – 7 + 40 + 27 + 9p = ±30
10p + 60 = ± 30
10p = -60 ± 30
p = −60±30 / 10
∴ Taking +ve sign, p = −60 + 30 / 10 = −30 / 10 = -3
Taking -ve sign, p = −60 − 30 / 10 = −90 / 10 = -9
Q3: If A(4, 2), B(7,6) and C(1, 4) are the vertices of a AABC and AD is its median, prove that the median AD divides AABC into two triangles of equal areas. [2022]
 View Answer
View Answer 
Sol:
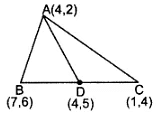
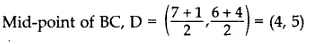
Area of ∆ABD
= 1/2 (x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= 1/2[4(6 – 5) + 7(5 – 2) + 4(2 – 6))
= 1/2(4 + 21 – 16) = 9/2 sq.units …(i)
Area of ∆ADC
= 1/2 [4(5 – 4) + 4(4 – 2) + 162 – 5)]
= 1/2(4 + 8 – 3) = 9/2sq.units
From (i) and (ii),
Area of ∆ABD = Area of ∆ADC
∴ Median AD divides ∆ABC into two triangles of equal area.
Q4: If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 or x + y = -9. [2021]
 View Answer
View Answer 
Sol:
Let A(x, y), B(1, 2), C(2, 1).
Area of ∆ABC = 6 sq. units …[Given
As 1/2 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 6
∴ x(2 – 1) + 1(1 – y) + 2(y – 2) = ±12
x + 1 – y + 2y – 4 = ±12
Taking +ve sign
x + y = 12 + 4 – 1
∴ x + y = 15
Taking -ve sign
x + y = -12 + 4 – 1
∴ x + y = -9
Q5: Point P(x, 4) lies on the line segment joining the points A(-5, 8) and B(4, -10). Find the ratio in which point P divides the line segment AB. Also find the value of x. [2020]
 View Answer
View Answer 
Sol: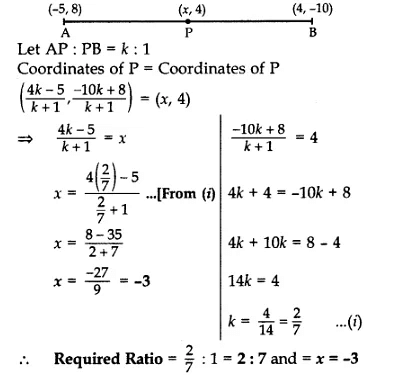
Q6: Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, -3). Also, find the value of x. [2019]
 View Answer
View Answer 
Sol:
Q7: If P(2, 4) is equidistant from Q(7, 0) and R(x, 9), find the values of x. Also find the distance P. [2018]
 View Answer
View Answer 
Sol: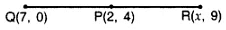 PQ = PR …[GivenPQ2 = PR2 … [Squaring both sides∴ (7 – 2)2 + (0 – 4)2 = (x – 2)2 + (9 – 4)2
PQ = PR …[GivenPQ2 = PR2 … [Squaring both sides∴ (7 – 2)2 + (0 – 4)2 = (x – 2)2 + (9 – 4)2
⇒ 25 + 16 = (x – 2)2 + 25
⇒ 16 = (x – 2)2
⇒ ±4 = x – 2 …[Taking sq. root of both sides
⇒ 2 ± 4 = x
⇒ x = 2 + 4 = 6 or x = 2 – 4 = -2
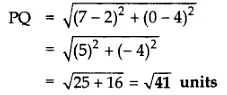
Q8: If the centroid of ∆ABC, in which A(a, b), B(b, c), C(c, a) is at the origin, then calculate the value of (a3 + b3 + c). [2018]
 View Answer
View Answer 
Sol: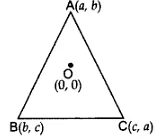 Centroid =
Centroid = 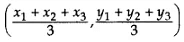
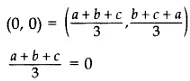 a + b + c = 0
a + b + c = 0
If a + b + c = 0
then, as we know
a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ac)
∴ a3 + b3 + c3 – 3abc = 0 … [Since a + b + c = 0
∴ a3 + b3 + c3 = 3abc …(Hence proved)
Q9: Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units. [2017]
 View Answer
View Answer 
Sol:
Let A(k + 1, 1), B(4, -3) and C(7, -k).
We have, Area of ∆ABC = 6 … [Given
6 = 1/2 [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
6 = 1/2[(k + 1)(-3 + k) + 4(-k – 1) + 7(1 + 3)]
12 = (-3k + k2 – 3 + k – 4k – 4 + 28]
12 = [k2 – 6k + 21]
⇒ k2 – 6k + 21 – 12 = 0
⇒ k2 – 6k + 9 = 0
⇒ k2 – 3k – 3k + 9 = 0
⇒ k(k – 3) – 3(k – 3) = 0 =
⇒ (k – 3) (k – 3) = 0
⇒ k – 3 = 0 or k – 3 = 0
⇒ k = 3 or k = 3
Solving to get k = 3.
Q10: For the triangle ABC formed by the points A(4, -6), B(3,-2) and C(5, 2), verify that median divides the triangle into two triangles of equal area. [2016]
 View Answer
View Answer 
Sol:
Let A(4, -6), B(3, -2) and C(5, 2) be the vertices of ∆ABC.
Since AD is the median
∴ D is the mid-point of BC.
⇒ D(3 + 5 / 2,−2 + 2 / 2) ⇒ D(4,0)
Area of ∆ABD
= 1/2 [4(-2 – 0) + 3(0 + 6) + 4(-6 + 2)]
= 1/2 [-8 + 18 – 16) = 1/2 [-6] = -3
But area of A cannot be negative.
∴ ar(∆ABD) = 3 sq.units …(i)
Area of ∆ADC
= 1/2 [4(0 – 2) + 4(2 + 6) + 5(-6 – 0)]
= 1/2(-8 + 32 – 30] = 12 [-6] = -3
But area of ∆ cannot be negative.
∴ ar(∆ADC) = 3 sq.units
From (i) and (ii),
∴ Median AD of AABC divides it into two ∆s of equal area.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths - Coordinate Geometry Previous Year Questions
| 1. What are the basic concepts of coordinate geometry? |  |
| 2. How is distance calculated in coordinate geometry? |  |
| 3. What is the equation of a line in coordinate geometry? |  |
| 4. How do we find the midpoint of a line segment in coordinate geometry? |  |
| 5. What are the applications of coordinate geometry in real life? |  |

















