Class 9 Science Chapter 10 Practice Question Answers - Work and Energy
Solved Important Examples
Q.1. A boy pushes a book by applying a force of 40N. Find the work done by this force as the book is displaced through 25 cm along the path.
Ans: Here, force acting on the book, F = 40N
distance through which book is displaced, s = 25 cm = 0·25 m
Work done by the force, i.e., W = F × s = (40 N) (0·25 m) = 10J
Q.2. A ball of mass 1 kg thrown upwards, reaches a maximum height of 4 m. Calculate the work done by the force of gravity during the vertical displacement. (g = 10 m/s2).
Ans: Here, force of gravity on the ball, F = mg = (1 kg) (l0 m/s2) = 10N
vertical displacement of the ball, s = 4m
Since the force and the displacement of the ball are in opposite directions, work done by the force of gravity, i.e., W= _F × s = _ (10N) (4m) = _ 40J
Obviously, work done against the force of gravity = 40J
Q.3. Find the amount of work done by a labourer who carries n bricks of m kilogram each to the roof of a house h metre high by climbing a ladder.
Ans: Here, force exerted by the labourer in carrying n bricks (each of mass m kg),
F = (mn) g = (mng) newton
displacement of the bricks, s = h metre
Work done by the labourer, W = F × s = (mng newton) × (h metre) = mngh joule
Q.4. An engine pulls a train 1 km over a level track. Calculate the work done by the train given that the frictional resistance is 5 × 105 N.
Ans: Here, frictional resistance, F = 5 × 105 N
distance through which the train moves, s = 1 km = 1000 m
Work done by the frictional force, i.e., W = _ Fs = _ (5 × 105 N) (1000 m) = - 5 × 108 J
(F and s are in opposite directions)
Obviously, work done by the train is 5 × 108 J
Q.5. A man weighing 70 kg carries a weight of 10 kg on the top of a tower 100 m high. Calculate the work done by the man. (g = 10 m/s2).
Ans: Here, force exerted by the man, F = (70 10) kg wt = 80 kg wt
= 80 × 10 N = 800 N (1 kg wt = 10 N)
vertical displacement, s = 100 m
Work done by the man, i.e., W = F × s = (800N) (100m) = 80000 J
Q.6. How fast should a man of mass 60 kg run so that his kinetic energy is 750 J ?
Ans: Here, mass of the man, m = 60 kg
kinetic energy of the man, Ek = 750J
If v is the velocity of the man, then
Ek = mv2
or v = 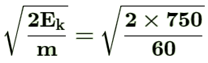 = 5 m/s
= 5 m/s
Q.7. Find the mass of the body which has 5J of kinetic energy while moving at a speed of 2 m/s.
Ans: Here, kinetic energy of the body, Ek = 5J
speed of the body, v = 2 m/s
If m is the mass of the body, then
Ek = mv2 or 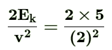 = 2.5 kg
= 2.5 kg
Q.8. A player kicks a ball of mass 250 g at the centre of a field. The ball leaves his foot with a speed of 10 m/s, Find the work done by the player on the ball.
Ans: The ball, which is initially at rest, gains kinetic energy due to work done on it by the player.
Thus, the work done by the player on the ball, W = kinetic energy (Ek) of the ball as it leaves his foot, i.e.,
W = Ek = mv2
Here, m = 250 g = 0·25 kg, v = 10 m/s
W = (0·25kg) (10 m/s)2 = 12·5 J
Q.9. A body of mass 5 kg, initially at rest, is subjected to a force of 20N. What is the kinetic energy acquired by the body at the end of 10s ?
Ans: Here, mass of the body, m = 5 kg
initial velocity of the body, u = 0
force acting on the body, F = 20 N
time for which the force acts, t = 10 s
If a is the acceleration produced in the body,
a = F/M - 20N/5Kg = 4 m/s2
Let v be the velocity of the body after 10 s.
Clearly, v = u at = 0 (4 m/s2) (10 s) = 40 m/s
Kinetic energy acquired by the body,
Ek = mv2 = (5kg) (40m/s)2 = 4000J
Q.10. A bullet of mass 20 g moving with a velocity of 500 m/s, strikes a tree and goes out from the other side with a velocity of 400 m/s. Calculate the work done by the bullet in joule in passing through the tree.
Ans: Here, mass of the bullet, m = 20 g = 0·02 kg
initial velocity of the bullet, u = 500 m/s
final velocity of the bullet, v = 400 m/s
If W is the work done by the bullet in passing through the tree, then according to work-energy theorem
W = mu2 _ mv2 = m(u2 _ v2)
or W = (0·02 kg) [(500 m/s)2 _ (400m/s)2] = 900J
Q.11. A body of mass 4 kg is taken from a height of 5 m to a height 10 m. Find the increase in potential energy.
Ans: Here, mass of the body, m = 4 kg
increase in height of the body, h = (10m _ 5m) = 5m
Increase in potential energy, Ep = mgh = (4 kg) (10 m/s2) (5m) = 200J
Aliter. Initial potential energy of the body, Epi = mgh = (4 kg) (10 m/s2) (5m) = 200J
Final potential energy of the body, Epf = mghf = (4 kg) (10 m/s2) (10 cm) = 400J
Increase in potential energy, Ep = Epf _ Epi = 400J _ 200J = 200J
Q.12. An object of mass 1 kg is raised through a height h. Its potential energy increases by 1 J. Find the height h.
Ans: Here, mass of the object, m = 1 kg increase in potential energy, Ep = 1J
As Ep = mgh, h = 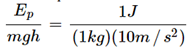 = 0·1 m
= 0·1 m
Q.13. A 5 kg ball is thrown upwards with a speed of 10 m/s.
(a) Find the potential energy when it reaches the highest point.
(b) Calculate the maximum height attained by it.
Ans: (a) Here, mass of the ball, m = 5 kg,
speed of the ball, v = 10 m/s
Kinetic energy of the ball, Ek =mv2 = (5kg)(10 m/s)2 =250J
When the ball reaches the highest point, Its kinetic energy becomes zero as the entire kinetic energy is converted into its potential energy (Ep) i.e., Ep = 250J
(b) If h is the maximum height attained by the ball,
Ep = mgh
From eqn. (i) and (ii), mgh = 250J
or = 5m
Q.14. A 5 kg ball is dropped from a height of 10m.
(a) Find the initial potential energy of the ball.
(b) Find the kinetic energy just before it reaches the ground and
(c) Calculate the velocity before it reaches the ground.
Ans: Here, mass of the ball, m = 5 kg
Height of the ball, h = 10m
(a) Initial potential energy of the ball,
Ep = mgh = (5 kg) (10 m/s2) (10m) = 500J
(b) When the ball reaches the ground, its potential energy becomes zero as it is entirely converted into its kinetic energy (Ek), i.e.,
Ek = 500J
(c) If v is the velocity attained by the ball before reaching the ground,
or Ek = mv2
V=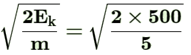 = 14·14 m/s
= 14·14 m/s
Q.15. A body is thrown up with a kinetic energy of 10 J. If it attains a maximum height of 5 m, find the mass of the body.
Ans: Here, kinetic energy of the body, Ek = 10J
maximum height attained by the body, h = 5m
When the body attains maximum height, its entire kinetic energy is converted into its potential energy
(Ep)' i.e., Ep = Ek
mgh = 10J
= 0.2 kg
Q.16. A rocket of mass 3 × 106 kg takes off from a launching pad and acquires a vertical velocity of 1 km/s and an altitude of 25 km. Calculate its (a) potential energy (b) kinetic energy.
Ans: Here, mass of the rocket, m = 3 × 106 kg
velocity acquired by the rocket, v = 1 km/s = 1000 m/s
height attained by the rocket, h = 25 km = 25000 m
(a) Potential energy of the rocket, Ep = mgh = (3 × 106 kg) (10 m/s2) (25000 m) =7·5 × 1011 J
(b) Kinetic energy of the rocket,
Ek = mv2 = (3 × 106 kg) (1000m/s)2 = 1·5 × 1012 J
Q.17. A boy of mass 40 kg runs up a flight of 50 steps, each of 10 cm high, in 5 s. Find the power developed by the boy.
Ans: Here, mass of the boy, m = 40 kg
total height gained, h = 50 × 10 cm = 500 cm = 5m
time taken to climb, t = 5s
Work done by the boy, W = mgh = (40 kg) (10 m/s2) (5m) = 2000J
Power developed, P = W/t - 2000J/5s = 400W
Q.18. What should be the power of an engine required to lift 90 metric tonnes of coal per hour from a mine whose depth is 200 m
Ans: Here, mass of the coal to be lifted, m = 90 metric tonnes = 90 × 1000 kg=9 × 104 kg
height through which the coal is to be lifted, h = 200m
time during which the coal is to be lifted, t = 1h = 60 × 60 = 3600 s
work done to lift the coal, i.e., W = mgh = (9 × 104 kg) (10 m/s2) (200m) = 18 × 107J
Power of the engine required i.e., P = 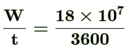 = 50000 W = 50 kW
= 50000 W = 50 kW
Q.19. How much time does it take to perform 500J of work at a rate of 10W ?
Ans: Here, work to be performed, W = 500J
rate at which work is to be performed, i.e., power, P = 10W
As P = W/t,
t = W/P = 500J/10W = 50 s
Q.20. Calculate the units of energy consumed by 100 W electric bulb in 5 hours.
Ans: Here, power of the electric bulb, P = 100 W = 0·1 kW
time for which bulb is used, t = 5h
As P = W/t, W = Pt
Energy consumed by the bulb, W = Pt = 0·1 kW (5 h) = 0·5 kWh = 0·5 units
Q.21. A lift is designed to carry a load of 4000 kg through 10 floors of a building, averaging 6 m per floor, in 10 s. Calculate the power of the lift.
Ans: Total distance covered by the lift, s = 10 × 6 m = 60 m
time in which this distance is covered, t = 10 s
force exerted by the lift, F = 4000 kg wt = 4000 × 10 N
= 4 × 104 N (1 kg wt = 10 N)
velocity of the lift, V = S/t - 60m/10s = 6 m/ s
Power of the lift, P = F v = (4 × 104 N) (6 m/s) = 24 × 104 W = 240 kW
Q.22. What kind of energy transformation takes place in the following cases?
(a) When water flowing down a dam runs a turbine to generate electricity.
(b) A running steam engine.
(c) Power generation in a thermal power station.
Ans:
(a) The scheme of energy transformation when water stored in a dam is used to produce electricity is,
Potential energy of water, Kinetic energy of flowing water, Kinetic energy turbine, Electricial energy.
Thus, in a hydropower station, the potential energy of water stored in a dam is converted into kinetic energy of the turbine which finally gets converted into electrical energy.
(b) The scheme of energy transformation in a running steam engine is,
Chemical energy of coal, Heat energy of steam, Kinetic energy of moving parts of the engine, Kinetic energy of the engine and boggies.
So, in a running steam engine, the scheme of energy transformation is,
Chemical energy, Heat energy, Kinetic energy
(c) The scheme of energy transformation in a thermal power station is,
Chemical energy of fuel (coal / diesel), Heat energy of steam, Kinetic energy of turbine, Electrical energy.
|
84 videos|478 docs|60 tests
|
FAQs on Class 9 Science Chapter 10 Practice Question Answers - Work and Energy
| 1. What is work and energy? |  |
| 2. How are work and energy related? |  |
| 3. What are some examples of work and energy in everyday life? |  |
| 4. How is work calculated? |  |
| 5. What is the principle of conservation of energy? |  |

















