Classification of Functions | Mathematics (Maths) Class 12 - JEE PDF Download
1. One-One Function (Injective mapping): A function f: A → B is said to be a one-one function or injective mapping if different elements of A have different f images in B. Thus for x1, x2 ∈ A & f(x1), f(x2) ∈ B, f(x1) = f(x2) ⇔ x1 = x2 or x1 ≠ x2 ⇔ f(x1) ≠ f(x2).
Diagrammatically an injective mapping can be shown as

OR 
Remark:
(i) Any function which is entirely increasing or decreasing in its domain, is one-one.
(ii) If any line parallel to the x-axis cuts the graph of the function at most at one point, then the function is one-one.
Q.1. Determine if the function given below is one to one.
(i) To each state of India assign its Capital
Ans. This is not one to one function because each state of India has not different capital.
(ii) Function = {(2, 4), (3, 6), (-1, -7)}
Ans. The above function is one to one because each value of range has different value of domain.
(iii) f(x) = |x|
Ans. Here to check whether the given function is one to one or not, we will consider some values of x (domain) and from the given function find the value of range(y).

From the above table we can see that an element in the range repeats, then this is not a one to one function.
Q.2. Without using graph prove that the function
F : R → R defiend by f (x) = 4 + 3x is one-to-one
Ans. For a function to be one-one function if
F (x1) = F (x1) ⇒ x1 = x2 ∀ x1, x2 ∈ domain
∴ Now f (x1) = f (x2) gives
4 + 3x1 = 4 + 3x2 or x1 = x2
∴ F is a one-one function.
(2) Many-One function: A function f: A → B is said to be a many one function if two or more elements of A have the same f image in B. Thus f: A → B is many one if for
x1, x2 ∈ A, f(x1) = f(x2) but x1≠ x2
Diagrammatically a many one mapping can be shown as

OR
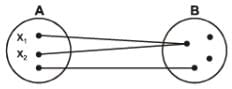
Remark:
(i) A continuous function f(x) which has at least one local maximum or local minimum, is many-one. In other words, if a line parallel to x-axis cuts the graph of the function at least at two points, then f is many-one.
(ii) If a function is one-one, it cannot be many-one and vice versa.
(iii) If f and g both are one-one, then fog and gof would also be one-one (if they exist).
Q.3. Without using graph check the following function f: R → R defined by f (x) = x2 is one-to-one or not ?
Ans. For the function to be one to one , different elements must have different images
But here if x = 1 then f(1) = (1)2 =1
And if x = -1 then f(-1) =(-1)2 = 1
Clearly, x = 1 and x = -1 both have same image
So given function is not one to one i.e many to one function
In other words, we can say that a function which is not one to one that can be known as many to one.
Example 16. Show that the function f(x) = (x2 - 8x + 18)/(x2 + 4x + 30) is not one-one.
Solution. Test for one-one function
A function is one-one if f(x1) = f(x2) ⇒ x1 = x2


Since f(x1) = f(x2) does not imply x1 = x2 alone, f(x) is not a one-one function.
Example 17. Let f be an injective function such that f(x) f(y) + 2 = f(x) + f(y) + f(xy) ∀ x, y ∈ R.
If f(4) = 65 and f(0) ≠ 2, then show that f(x) – 1= x3 for x ∈ R
Solution. Given that f(x) f(y) + 2 = f(x) + f(y) + f(xy) ....(i)
Putting x = y = 0 in equation (i), we get f(0) f(0) + 2 = f(0) + f(0) + f(0)
or (f(0))2 + 2 = 3f(0) or (f(0) – 2) (f(0) – 1) = 0 or f(0) = 1 (∴ f(0) ≠ 2) ....(ii)
Again putting x = y = 1 in equation (i) and repeating the above steps, we get (f(1) – 2) (f(1) – 1) = 0
But f(1) ≠ 1 as f(x) is injective.
∴ f(1) = 2 ...(iii)
Now putting y = 1/x in equation (i), we get






Let f(x) – 1 = g(x)

from equation (iv), we get g(x) g(1/x) = 1 which is only possible when
g(x) = ± xn
f(x) = ± xn + 1
or f(x) = ± xn + 1 or 65 = ± 4n + 1
or 4n = 64 = (4)3
n = 3
f(x) = x3 + 1 or f(x) – 1 = x3 (neglecting negative sign)
3. Onto-function (Surjective mapping): If the function f: A → B is such that each element in B (co-domain) is the f image of at least one element in A, then we say that f is a function of A 'onto' B. Thus f: A → B is surjective if ∀ b ∈ B, ∃ some a ∈ such that f (a) = b.
Diagramatically surjective mapping can be shown as

OR
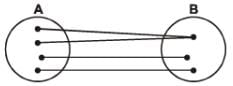
Note that: if range ≡ co-domain, then f(x) is onto.
Q.4. If f: R → R is defined as f (x)= 3x + 7, x ∈ R, then show that f is an onto function.
Ans. We have f (x) = 3x + 7, x ∈ R . Let b ∈ R so that f (x) = b ⇒ 3x + 7 = b or
x = (b - 7)/3. Since b ∈ R, (b - 7)/3 ∈ R.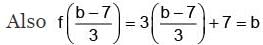
⇒ b is image of (b - 7)/3 where b is arbitrary.
Hence f (x) is an onto function.
4. Into function: If f: A → B is such that there exists at least one element in co-domain which is not the image of any element in the domain, then f(x) is into.
Diagramatically into function can be shown as

Remark:
(i) If a function is onto, it cannot be into and vice versa.
(ii) If f and g are both onto, then gof or fog would be onto (if exists).
Thus a function can be one of these four types:
(a) One-one onto (injective & surjective)

(b) One-one into (injective but not surjective)

(c) Many-one onto (surjective but not injective)

(d) many-one into (neither surjective nor injective)

Remark:
(i) If f is both injective & surjective, then it is called a Bijective function. Bijective functions are also named as invertible, non singular or biuniform functions.
(ii) If a set A contains n distinct elements then the number of different functions defined from A → A is nn & out of it n ! are one-one.
(iii) The composite of two bijections is a bijection i.e. if f & g are two bijections such that gof is defined, then gof is also a bijection.
Q. Prove that
F : R → R defined by f (x) = 4x3 - 5 is a bijection
Ans. Now f (x1) = f (2) ∀ x1, x2 Domain
∴ 4x1 3 - 5 = 4x23 - 5
⇒ x1 3 = x23
⇒ x1 3 - x23 = 0 ⇒ (x2 - x1) (x12 + x1x2 + x22) = 0
⇒ x1 = x2 or
x12 + x1x2 + x22 = 0 (rejected).
It has no real value of x1 and x2.
∴ F is a one-one function.
Again let y = (x) where y ∈ codomain, x ∈ domain.
We have y = 4x3 - 5
or 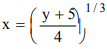
∴ For each y ∈ codomain ∃ x ∈ domain such that f (x) = y.
Thus F is onto function.
∴ F is a bijection.
Example 18. A function is defined as , f: D → R f(x) = cot-1 (sgn x) + sin-1(x - {x}) (where {x} denotes the fractional part function) Find the largest domain and range of the function. State with reasons whether the function is injective or not. Also draw the graph of the function.
Solution. f is many one


Example 19. Find the linear function(s) which map the interval [0 , 2 ] onto [1 , 4 ].
Solution. Let f (x) = a x + b
f (0) = 1 & f (2) = 4 ⇒ b = 1 & a =3/2
or f (0) = 4 & f (2) = 1 ⇒ b = 4 & a = -3/2
f(x) = 3x/2 + 1 or f(x) = 4 - 3x/2
Example 20.
(i) Find whether f(x) = x + cos x is one-one.
(ii) Identify whether the function f(x) = -x3 + 3x2 - 2x + 4 ; R → R is ONTO or INTO
(iii) f(x) = x2 - 2x + 3; [0, 3] → A. Find whether f(x) is injective or not.
Also find the set A, if f(x) is surjective.
Solution.
(i) The domain of f(x) is R. f'(x) = 1 – sin x.
f'(x) ≥ 0 for all x ∈complete domain and equality holds at discrete points only
∴ f(x) is strictly increasing on R. Hence f(x) is one-one
(ii) As codomain ≡ range, therefore given function is ONTO
(iii) f'(x) = 2(x – 1); 0 ≤ x ≤ 3


f(x) is a non monotonic continuous function. Hence it is not injective.
For f(x) to be surjective, A should be equal to its range. From graph, range is [2, 6]
∴ A ≡ [2, 6]
Example 21. If f and g be two linear functions from [-1, 1] onto [0, 2] and  be defined by
be defined by

Solution. Let h be a linear function from [-1, 1] onto [0, 2].
Let h(x) = ax + b, then h'(x) = a
If a > 0, then h(x) is an increasing function & h(–1) = 0 and h(1) = 2 ⇒ –a + b = 0 and a + b = 2 ⇒ a = 1 & b = 1.
Hence h(x) = x + 1.
If a < 0, then h(x) is a decreasing function & h(–1) = 2 and h(1) = 0 ⇒ –a + b = 2 and a + b = 0 ⇒ a = –1 & b = 1.
Hence h(x) = 1 – x
Now according to the question f(x) = 1 + x & g(x) = 1 - x
or f(x) = 1 – x & g(x) = 1 + x


 ,
, 
In both cases, |Ø(Ø(x)) + Ø(Ø(1/x)) | 
|
204 videos|290 docs|139 tests
|
FAQs on Classification of Functions - Mathematics (Maths) Class 12 - JEE
| 1. What is the classification of functions? |  |
| 2. How are linear functions classified? |  |
| 3. What are the characteristics of quadratic functions? |  |
| 4. How are exponential functions classified? |  |
| 5. What are the classifications of trigonometric functions? |  |

|
Explore Courses for JEE exam
|

|


















