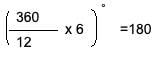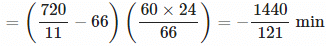Important Formulas: Clocks | CSAT Preparation - UPSC PDF Download
Facts About Clock
A Clock is a circular device provided with three hands viz. an hour hand, minute and second hand.
All hands move around the circular dial. The hour hand is smaller than the minute hand and the hour hand is slower than the minute hand. The hour hand shows time in hours and the minute hand shows time in minutes.
The clock is separated into 12 equal pieces with numbers ranging from 1 to 12.
360/12 = 30° for each section.
One hour is when the minute hand completes a full round, i.e., covers 360°.
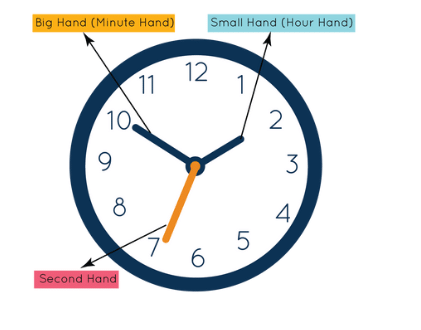
Structure of Clock
- Dial: The dial of a clock is circular. The dial’s periphery is numbered 1 through 12 to indicate the hours in a 12-hour cycle. A dial’s diameter is divided into 60 equal minute spaces or 12 equal hour spaces.
- Minute Spaces: The face or dial of a watch is circular, divided into 60 equal pieces, known as minute spaces.
- Hour Hand and Minute Hand: Clocks contain two hands, the smaller of which is known as the hour hand or shorthand, and the larger of which is known as the minute hand.
- Second hand: On the circular dial, the second hand represents seconds. It rotates at a rate of one per minute.
- Overlap: Once every hour, both hands will coincide.
- Straight Line: When the hands are parallel or opposed to each other, they form a straight line.
 12 Equal Divisions of a Clock
12 Equal Divisions of a Clock
The angle between any two consecutive divisions = (360°)/12= 30°
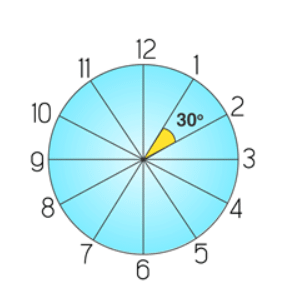 Angle Divisions of a clock
Angle Divisions of a clock
Clocks Important Conversions
Few formulas that you should know to solve questions related to clocks are as follows:
- 60-minute space = 360° = 1 hour
- 1-minute space = 6°
2-minute space = 6° x 2 = 12°
3-minute space = 6° x 3 = 18°
- Right Angle or Perpendicular = 15-minute spaces apart
There are 22 times right angles in 12 hours or 44 times in 24 hours (1 day) - Speed of minute hand = 6 dpm(degree per minute)
- Straight Angle or Straight Line or 180° = 30-minute space apart
Straight Angle takes place 11 times in 12 hours or 22 times in 24 hours (1 day) - Angle traced by hour hand in 12 hrs = Angle traced by the minute hand in 60 min. = 360°.
- Speed of hour hand = 0.5 dpm (degrees per minute)
- The angle of the hour hand from vertical at N o’clock = 30N
Comparison of Speed of Hands
The difference in the speed = 6°– (1/2°) = 5.5° per minute
Comparing the speed of the minute hand and the hour hand, one can conclude that the minute hand is always faster than the hour hand by 5.5° or the hour hand is always slower than the minute hand by 5.5°
Note: The evaluation of the speed of second hands is not necessary as it travels a corresponding distance of 1 second in a second.
Frequency of coincidence and collision of the hands of a clock:
As we know, the hands of clock move at different speeds, they coincide and collide and also make different angle formations among themselves at various times in a day.
Q: How many times in a day do the minute and hour hands of a clock coincide (Angle between them is zero) with each other?
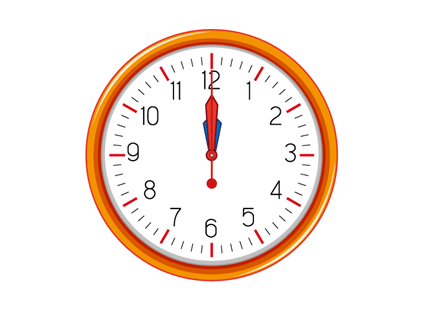
- A first collision of the hands of a clock at midnight
- A day starts at midnight, and hence, the first-ever coinciding of hands happens at midnight. Now observing the clock, the next coincidence will occur at approximately 1 o’clock and 5 minutes. Thus, one can conclude that every hour, there is one coincidence of hands. Therefore, the answer should be 24 times for 24 hours. But it is not the correct answer and the right logic.
- Now observe the time between 11 to 12, it can either be A.M or P.M, the hands are not coinciding between 11’o o’clock and 12’o o’clock. The coincidence of hands at 12’ o clock is the coincidence between 12 and 1 and 11 and 12. Hence, in 12 hours, there will only be 11 coincidence. Extending the logic for 24 hours of the day, there will be 22 coincidences.
- If 12:0:0 A.M is the first coincidence of the hands in a day then the next collision will be at 1’o o’clock 5 minutes, but the evaluation of seconds is difficult, but not impossible.
- We know that in 12 hours, there will be 11 coincidences. Therefore, one collision will happen at:
- Frequency of one collision = (12 hours)/11
- Frequency of one collision = (12*60 mins)/11
- Frequency of one collision = (720 mins)/11
- Frequency of one collision = 65(5/11)
- The value 65(5/11) indicates that the hands of a clock coincide after every 65 minutes 5/11 of a minute. i.e. if 12:0:0 is the first collision, then the exact time of the next collision will be obtained by adding 65(5/11) to 12 o’clock.
Q: How many times in a day do the minute and hour hands of clock form a 180° straight line in a day?
- The hands of the clock make one 180° straight line every hour except between 5’o clock and 6’o clock. A precise observation and analysis of the watch gives the idea that between 5 and 6 the hands make straight line 180° exactly at 6 o’clock and hence, it cannot be the one which happens between 5 o’clock and 6 o’clock. Instead it is considered as a straight line formed between 6 and 7 o’clock.
- Therefore, the hands of a clock make 180° straight lines 11 times in 12 hours and hence generalising it for 24 hours, the hands make 22 consecutive lines of 180° in 24 hours.
Finding the Time when the Angle is Known
When the angle between the hands are not perfect angles like 180°, 90° or 270°, solving such questions becomes difficult and time-consuming at the same time. The logic below provides a trick to address problems involving angles of hands for other than standard aspects.
T = 2/11 [H*30±A]
Where:
1. T stands for the time at which the angle formed.
2. H stands for an hour, which is running.
(If the question is for the duration between 4 o’clock and 5 o’clock, it’s the 4th hour which is running hence the value of H will be ‘4’.)
3. A stands for the angle at which the hands are at present.
(The value of A is provided in the question generally)
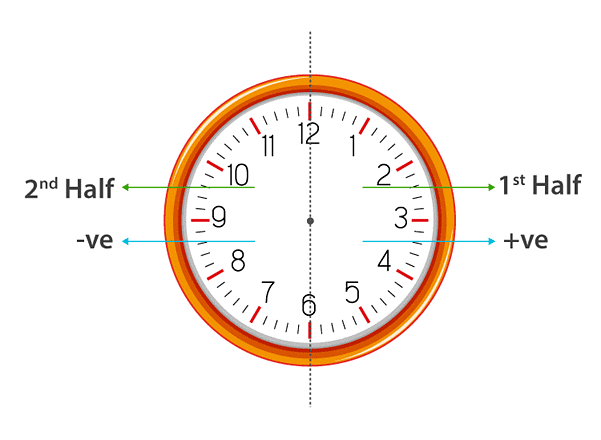
The clock is divided into two parts: 1st and 2nd half as shown above
If the time given in the question lies in the first half, then the positive sign is considered while evaluating the time else, the negative sign is used.
Q: At what time between 3 and 4 o’clock, the hands make an angle of 10 degrees?
Solution:
Given: H = 3 , A = 10
Since both three and four lies in the first half considered a positive sign.
Calculations:
T = 2/11 [H*30±A]
T = 2/11 [3*30+10]
T = 2/11 [90+10]
T = 2/11 [100]
T = 200/11
T =18 2/11
The answer indicates that the hands of a clock will make an angle of 10 between 3 and 4 o’clock at exactly 3:18:2/11 ( 3’ o clock 18 minutes and 2/11 of minutes = 2/11*60 = 10.9 seconds)
Correct Clock v/s Wrong Clock
This section involves the comparison of time in the accurate clock with the wrong watch. The wrong time indicates that a clock is either slow or fast compared to the correct time. The wrong clock can either be fast or delayed by a few seconds/minutes/ hours or sometimes by a few days and weeks.
Q: A clock gains 5 seconds for every 3 minutes. If the clock started working at 7 a.m. in the morning, then what will be the time in the wrong clock at 4 p.m. on the same day?
Solution:
- A clock gains 5 seconds for every 3 minutes, then it will gain 50 seconds in 30 minutes, or it will acquire 100 seconds in 60 minutes. i.e. it will gain 100 seconds in 1 hour. Since the clock was started at 7 a.m. in the morning and right now the correct time is 4 p.m. the total time the clock has worked is 9 hours.
- We know that in 1 hour it gains 100 seconds, then in 9 hours it increases 900 seconds. The conversion of 900 seconds to minutes will be 15 minutes. This increase indicates that the clock is faster by 15 minutes, as the clock is gaining.
- Hence, the time on the watch would be 4:15 p.m.
Points to Remember
- Minute Spaces: The face or dial of the clock is a circle whose circumference is divided into 60 equal parts, named minute spaces.
- The hour hand and minute hand
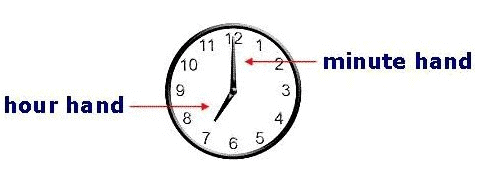 The smaller hand is called the hour hand or shorthand and the larger one is called the minute hand or longhand.
The smaller hand is called the hour hand or shorthand and the larger one is called the minute hand or longhand. - In 60 minutes, the minute hand gains 55-minute spaces over the hour hand.
(In 60 minutes, the hour hand will move 5-minute spaces while the minute hand will move 60-minute spaces. In effect the space gain of minute hand with respect to hour hand will be 60 - 5 = 55 minutes.) - Both the hands of a clock coincide once every hour.
Example: Between 11 and 1'o clock, hands are together as shown in the adjacent figure.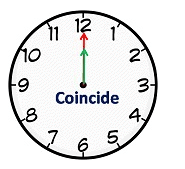
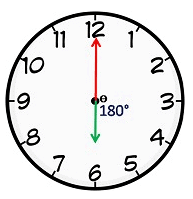
- The hands of a clock are in the same straight line when they are coincident or opposite to each other. If two hands are in opposite directions. (180° apart), then they are 30 min spaces apart. This happens once in 1 h. In a period of 12 hours, both hands are in opposite direction 11 times and in a day both hands are in opposite direction 22 times.
- When the two hands of a clock are at right angles, they are 15-minute spaces apart.
This happens twice in 1 h. In a period of 12 h, the hands are at a right angle 22 times (2 common positions) and in a day both hands are at a right angle 44 times.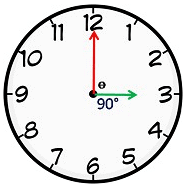
- When the hands of a clock are in opposite directions, they are 30-minute spaces apart.
- Angle traced by hour hand in 12 hrs = 360°
- Angle traced by minute hand in 60 min. = 360°.
- If a watch or a clock indicates 9.15, when the correct time is 9, it is said to be 15 minutes too fast.
- If a watch or a clock indicates 8.45, when the correct time is 9, it is said to be 15 minutes too slow.
- The hands of a clock will be in a straight line but opposite in direction, 22 times in a day.
- (i) The hands of a clock coincide 22 times in a day.
(ii) The hands of a clock are straight 44 times in a day.
(iii) The hands of a clock are at right angles 44 times a day.
Tricks
- The minute hand of a clock overtakes the hour hand at intervals of M mins of correct time. The clock gains or losses in a day by:
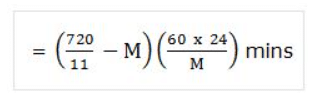
- The angle between the hands of a clock-
(a) Case 1: When the minute hand is behind the hour hand, the angle between the two hands at M mins past H O’clock:
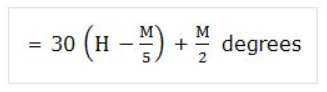
(b) Case 2: When the minute hand is ahead of the hour hand, the angle between the two hands at M mins past H O’clock: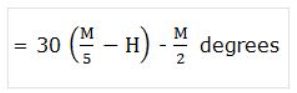
The two hands of the clock will be at right angle between H and (H + 1) O’clock at :
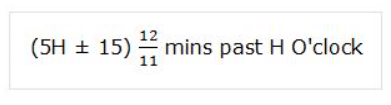
(a) Case 1: When the minute hand is 15 mins spaces behind the hour hand, to be in this position, the minute hand will have to gain (5H – 15) mins spaces over the hour hand.
(b) Case 2: When the minute hand is 15 mins spaces ahead of the hour hand, to be in this position, the minute hand will have to gain (5H + 15) mins spaces over the how hand.
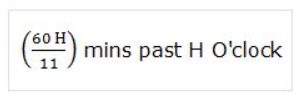
The two hands of the clock will be in the same straight line but not together between H and (H + 1) O’clock at :

The two hands of the clock will be together between H and (H + 1) O’clock at:
Solved Problems
Example 1: At what time between 4 and 5, the minute hand will be 2 minutes spaces ahead of the hour hand?
Ans: At 4 O'clock, the two hands are 20 min spaces apart.
In this case, the min hand will have to gain (20 + 2) i.e. 22 – minute spaces.
So, 22 – minute spaces will be gained in (60/55) × 22 = 24 min.
Example 2: The minute hand of a clock overtakes the hour hand at intervals of 65 minutes of correct time. How much does the clock lose or gain in 12 hours?
Ans: In a correct clock, the minute hand and hour hand should meet after every 65 5/11 min.
But we know that they are meeting after every 65 minutes.
So, the gain in 65 minutes is 5/11 minutes.
Gain in 12 hours = (120 × 60/65) × (5/11) = 720/143 = 5 5/143 min.
Example 3: A clock is set right at 10 am. The clock gains 5 minutes in 12 hours. What will be the true time when the clock indicates 3 pm on the next day?
Ans: Time from 10 am to 3 pm on the following day is 29 hrs.
Now, 12 hrs 5 min i.e. 145/12 hrs of this clock = 12 hours of correct clock.
So, 29 hours of this clock is (29 × 12 × 12)/145 = 144/5 = 28 hours 48 minutes.
So, the time is 12 minutes before 3 pm.
Example 4: The minute hand of a clock overtakes the hour band at interval of 60 mins. How much a day does the clock gain or lose?
Ans: In a correct clock, minute hand gains 55 minute spaces over the hour hand in 60 minutes.
Therefore, 60 min spaces are gained in (60 × 60)/55 = 720/11 minutes.
In other words, minute hand overtakes hour hand in every 720/11 minutes.
In the example given, minute hand overtakes hour band in 60 minutes.
Therefore, gain in 60 minute = (720/11) - 60 = 60/11 minutes.
Gain in 24 hours = (60/11) × 24 = 1440/11 min
gain/loss =
Since the sign is +ve, clock gains 1440/11 min in a day.
Example 5: The minute hand of a clock overtakes the hour band at an interval of 66 mins. How much a day does the clock gain or lose?
Ans: As we have seen previously, minute hand overtakes hour hand in every 720/11 minute.
In this example, minute hand overtakes hour band in 66 minutes
Therefore, loss in 66 minute = 66 - 720/11 = 6/11 minutes
Loss in 24 hours = 6/11 × 1/66 × 66 × 24 = 1440/121 min
gain/loss
Since the sign is -ve, the clock loses 1440/121 min a day.
Example 6: What is the angle between the hands of the clock at 7:20. At 7 o’ clock, the hour hand is at 210 degrees from the vertical.
Ans: In 20 minutes, Hour hand = 210 + 20*(0.5) = 210 + 10 = 220 {The hour hand moves at 0.5 dpm}
Minute hand = 20*(6) = 120 {The minute hand moves at 6 dpm}. Difference or angle between the hands = 220 – 120 = 100 degrees.
Example 7: A watch gains 5 seconds in 3 minutes and was set right at 8 AM. What time will it show at 10 PM on the same day?
Ans: The watch gains 5 seconds in 3 minutes => 100 seconds in 1 hour. From 8 AM to 10 PM on the same day, time passed is 14 hours. In 14 hours, the watch would have gained 1400 seconds or 23 minutes 20 seconds. So, when the correct time is 10 PM, the watch would show 10 : 23 : 20 PM
|
205 videos|258 docs|136 tests
|
FAQs on Important Formulas: Clocks - CSAT Preparation - UPSC
| 1. How can the structure of a clock help in solving clock-related problems? |  |
| 2. What are some important conversions to keep in mind when dealing with clocks? |  |
| 3. How can one compare the speed of the hour and minute hands on a clock? |  |
| 4. How can one find the time when the angle between the hour and minute hands is known? |  |
| 5. What are some key differences between a correct clock and a wrong clock in clock-related problems? |  |