Cohesionless & Cohesive Soils - Slope Stability, Soil Mechanics | Soil Mechanics Notes- Agricultural Engineering PDF Download
Cohesionless Soil
For cohesionless soil, the shear strength can be written as:
\[{\tau _f}={\sigma _n}\tan \phi '=\gamma \,z{\cos ^2}\beta \tan \phi '\] (28.4)
where tf is the failure shear strength and ø' is the angle of shearing resistance or angle of internal friction.
Thus, factor safety (F) can be written as:
\[F={{Shear\;Strength} \over {Shear\;Stress}}={{\gamma \,z{{\cos }^2}\beta \tan \phi } \over {\gamma \,z\cos \beta \sin \beta }}={{\tan \phi '} \over {\tan \beta }}\] (28.5)
Figure 28.3 shows the effective forces acting on an element in the infinite slope. The position of water table is also shown in the figure. The effective normal stress can be written as:
\[{\sigma '_n}={{(W-{\gamma _w}hb\cos\beta )\cos\beta}\over b}=(\gamma\,z\cos\beta-{\gamma _w}h\cos\beta)\cos\beta\]
\[=(\gamma \,z - {\gamma _w}h){\cos ^2}\beta\] (28.6)
\[\tau={{W\sin \beta } \over b}=\gamma \,z\cos \beta \sin \beta\] (28.7)
where Yw is the unit weight of water.
\[F={{Shear\;Strength}\over{Shear\;Stress}}={{{{\sigma '}_n}\tan \phi}\over\tau }={{(\gamma \,z - {\gamma _w}h){{\cos }^2}\beta\tan\phi}\over{\gamma \,z\cos \beta \sin \beta }}=\left({1 - {{{\gamma _w}h}\over {\gamma \,z}}} \right){{\tan\phi '}\over{\tan\beta}}\] (28.8)
If water table is at the top i.e z=h then,
\[F=\left({1 - {{{\gamma _w}} \over \gamma }} \right){{\tan \phi '}\over{\tan \beta }}\] (28.9)
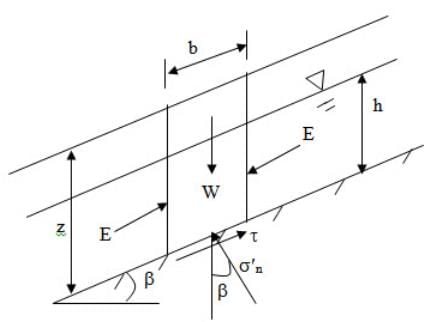
Fig. 28.3. . Effective forces acting on an element in the infinite slope.
Cohesive Soil
In case of c-ø soil, the shear strength can be written as:
\[{\tau _f}=c' + {\sigma _n}\tan \phi '=c' + \gamma \,z{\cos ^2}\beta \tan \phi '\] (28.10)
\[F=={{c' + \gamma \,z{{\cos }^2}\beta \tan \phi '} \over {\gamma z\cos \beta \sin \beta }}\] (28.11)
For F = 1, the depth z is called as critical depth (hc). Thus, putting F=1 and z=hc in Eq. (28.11), one can get
\[{h_c}={{c'} \over {\gamma (\tan \beta-\tan \phi '){{\cos }^2}\beta }}\] (28.12)
For seepage parallel to the slope,
\[F={{c' + (\gamma z - {\gamma _w}h){{\cos }^2}\beta \tan \phi'}\over{\gamma z\cos\beta\sin\beta }}\] (28.13)
\[{h_c} = \frac{{c'}}{{\gamma (\tan\beta-\frac{{{\gamma _w}}}{\gamma}\tan\varphi '){{\cos}^2}\beta}}\] (28.14)
The stability number (Sn) can be written as:
\[{S_n}={{c'} \over {\gamma {h_c}}}=(\tan \beta-\tan \phi '){\cos ^2}\beta\]

|
Explore Courses for Agricultural Engineering exam
|

|
















