Colligative Properties & Relative Lowering in V.P | Additional Study Material for JEE PDF Download
COLLIGATIVE PROPERTIES
These are the properties of solutions which depend upon the relative number of solute particles (molecules or ions) but not upon their nature.
These are
- Relative lowering of vapour pressure
- Elevation of boiling point
- Depression in freezing point and the
- Osmotic pressure
These arise due to the presence of a non - volatile solute.
Key concept: In dilute solutions these properties depend only on the number of solute particles present and not on their identity. For this reason they are called colligative properties (denoting depending on the collection).
We shall assume throughout the following that.
(i) The solute is non - volatile.
(ii) The solute does not dissolve in the solid solvent (the pure solid separates when the solution is frozen).
FIRST COLLIGATIVE PROPERTY
Relative Lowering of Vapour Pressure
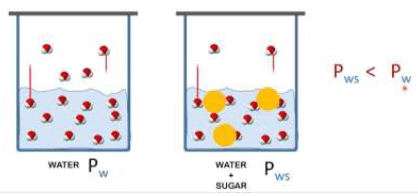
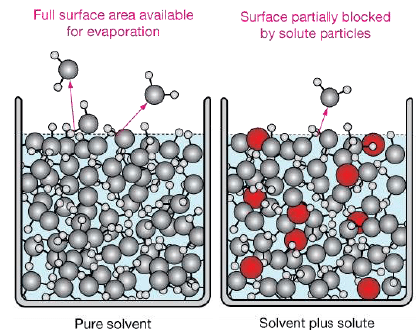
When a non volatile solute is present in the solution, the vapour pressure of the solution will be less than vapour pressure of pure solvent.
According to the Raoult's law, Psolvent = Xsolvent Pºsolvent,
Where Psolvent is the vapour pressure of the liquid solution, Xsolvent is its mole fraction in the solution and Pºsolvent is the pure vapour pressure.
If a solution is formed by dissolving ‘n’ moles of a non volatile solute in ‘N’ moles of a volatile solvent. Then
Mole fraction of solvent, X1 = N/n + N
Mole fraction of solute X2 = n/N + n
Since the solute is non – volatile, so it would have negligible vapour pressure and thus the vapour pressure of the solution, is approximately same as the vapour pressure of the solvent.
According to Raoult’s law
P1 = X1 P01 ...(i)
Since X1 + X2 = 1 so X1 = 1 − X2
Now P1 = (1− X2)P10
Or
P01P1 /P01 = X2 ...(ii)
In equation (ii) P10 −P1 is the vapour pressure lowering and (P10 − P1) / P10 is the relative vapour pressure lowering. From equation (ii) it is clear that the relative vapour pressure lowering is proportional to the mole fraction of the non – volatile solute in solution. It is independent of the nature of the solute. The relative vapour pressure lowering is, therefore a colligative property.
The mole fraction, X2 = n/n + N
For a dilute solution, the number of moles of the solute (n) can be neglected as compared to the number of moles of the solvent (N). Hence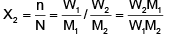
Where W1 is the amount of the solute dissolved in W1 amount of solvent, M1 is the molar mass of the solvent and M2 is the molar mass of the solute.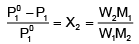
Vapour pressure in terms of molality of the solution:
where m is the molality
Key concept: The mole fraction of any substance does not change with temperature. So the mole fraction of the solute (Xsolute) does not change with temperature. Then, according to above expression the relative lowering of the vapour pressure should be independent of temperature. This is found to be so only for dilute solutions. Therefore, the Raoult's law, in this form, is applicable to the dilute solutions of non-volatile and non-electrolytic solutes only.
OSTWALD - WALKER EXPERIMENT
When air is passed through any gas, the gas diffuses into the air due to the principle of diffusion till the pressure of the gas in the air is equal to that of the gas outside. Therefore as air is passed through the solution, it absorbs the vapours of the solvent till the pressure of the solvent vapours in the air is P (vapour pressure of solvent in the solution).
Mass of vapour absorbed or loss in weight of solution = PVm/RT
Where, P = pressure of the solvent vapours,
V = volume available for vapours in the solution bulb,
T = temperature of the bulb and
m = molecular weight of the solvent.
As the air passes through the solvent, the pressure difference of the vapours in the air and outside is P0 - P. So the air absorbs this amount of vapours and gets saturated.
Loss in weight of solvent bulb = (P° - P)Vm/RT
As the sum of the losses of weight in the two containers is equal to the gain in weight of CaCl2,
Gain in weight of CaCl2 filled tubes = P°Vm/RT
.
Method
In this method a stream of dry air is passed successively through (i) a solution (ii) the pure solvent (water) and (iii) a reagent (anhydrous CaCl2) which can absorb the vapours of the solvent. The complete assembly is shown in figure, given below:
The first three bulbs contain a weighed amount of the solution under examination and the next three bulbs contain a weighed amount of the pure solvent.
A weighed amount of CaCl2 is taken in the set of U - tubes at the end. All the bulbs are at the same temperature and the volume available for the vapours in the solution and solvent bulbs are same temperature and the volume available for the vapours in the solution and solvent bulbs are same.
Key concept: It is designed in order to calculate the relative lowering of vapour pressure of a solvent due to a non - volatile solute.
Example 1. 0.5 g of a non-volatile organic substance was dissolved in 100 mL of CCl4 at 30°C. The vapour pressure of the solution was found to be 141.9 torr. Calculate the molar mass of the substance if the vapour pressure of CCl4 at 30°C is 143 torr and its density is 1.58 g mL - 1.
Solution.
Simplifying this,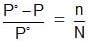

or M = 62.86 g/mol
Example 2. The vapour pressure of pure benzene at 20°C is 639.7 mm of Hg and the vapour pressure of a solution of a solute in C6H6 at the same temperature is 631.9 mm of Hg. Calculate molality of solution.
Solution.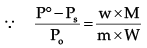
∴ Molality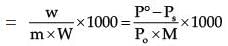
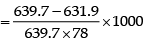
= 0.156 mol/kg of solvent
Example 3. The vapour pressure of a solvent decreased by 10 mm Hg when a non volatile solute was added to the solvent. The mole fraction of solute in solution is 0.2, what would be mole fraction of the solvent if decrease in vapour pressure is 20 mm of Hg.
(a) 0.8
(b) 0.6
(c) 0.4
(d) 0.2
Ans. (b)
Solution.
Po – Ps = Po × mole fraction of solute; 10 = Po × 0.2 Again, 20 = Po × mole fraction solute Hence, n = 0.4, so, mole fraction of solvent = 1 – 0.4 = 0.6
Example 4. The density of a 0.438 M solution of potassium chromate at 298 K is 1.063 g cm-3. Calculate the vapour pressure of water above this solution.
Given: P0 (water) = 23.79 mm Hg.
Solution.
A solution of 0.438 M means 0.438 mol of K2CrO4 is present in 1L of the solution. Now,
Mass of K2CrO4 dissolved per litre of the solution = 0.438 × 194 = 84.972 g
Mass of 1L of solution = 1000 × 1.063 = 1063 g
Amount of water in 1L of solution = 978.028
Assuming K2CrO4 to be completely dissociated in the solution, we will have;
Amount of total solute species in the solution = 3 × 0.438 = 1.314 mol.
Mole fraction of water solution = 54.335/54.335 + 1.314 = 0.976
Finally, Vapour pressure of water above solution = 0.976 × 23.79
= 23.22 mm Hg
TRY YOURSELF!
Q.1. 10 gm of a solute is dissolved in 80 gm of acetone (V.P. of this solution = 271 mm of Hg). If V.P. of pure acetone is 283 mm of Hg. Calculate molar mass of solute.
Ans. 163 gm/mol.
Q.2. Vapour pressure of solute containing 6 gm of non volatile solute in 180 gm of water is 20 Torr/mm of Hg. If 1 mole of water is further added, the V.P. increses by 0.02 torr. Calculate V.P of pure water & molecular wt. of non volatile solute.
Ans. P˚ =20.22 Torr.
m = 54 gm/mol.
|
22 videos|163 docs|17 tests
|
FAQs on Colligative Properties & Relative Lowering in V.P - Additional Study Material for JEE
| 1. What are colligative properties? |  |
| 2. How is relative lowering in vapor pressure related to colligative properties? |  |
| 3. What is the significance of colligative properties in the JEE exam? |  |
| 4. How can one calculate the relative lowering in vapor pressure? |  |
| 5. Can you give an example of a JEE-level question related to colligative properties and relative lowering in vapor pressure? |  |





















