Common Subexpression Elimination | Compiler Design - Computer Science Engineering (CSE) PDF Download
15-411: Compiler Design Frank Pfenning
➤ Introduction
Copy propagation allows us to have optimizations with this form: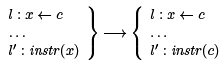
It is natural to ask about transforming a similar computation on compound expressions:
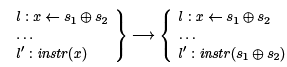
However, this will not work most of the time. The result may not even be a valid instruction (for example, if instr (x) = (y x ⊕ 1). Even if it is, we have made our program bigger, and possibly more expensive to run. However, we can consider the opposite: In a situation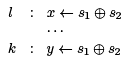
we can replace the second computation of s1 ⊕ s2 by a reference to x (under some conditions), saving a reduction computation. This is called common subexpression elimination (CSE).
➤ Common Subexpression Elimination
The thorny issue for common subexpression elimination is determining when the optimization above is performed. Consider the following program in SSA form: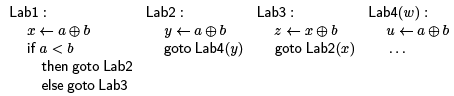
If we want to use CSE to replace the calculation of a ⊕ b in Lab4, then there appear to be two candidates: we can rewrite u a ⊕ b as u x or u y. However, only the first of these is correct! If control flow passes through Lab3 instead of Lab2, then it will be an error to access x in Lab4.
In order to rewrite u a ⊕ b as u x, in general we need to know that x will have the right value when execution reaches line k. Being in SSA form helps us, because it lets us know that the right-hand sides will always have the same meaning if they are syntactically identical. But we also need to know x even be defined along every control flow path that takes us to Lab4.
What we would like to know is that every control flow path from the beginning of the code (that is, the beginning of the function we are compiling) to line k goes through line l. Then we can be sure that x has the right value when we reach k. This is the definition of the dominance relation between lines of code. We write l ≥ k if l dominates k and l > k if it l strictly dominates k. We see how to define it in the next section; once it is defined we use it as follows: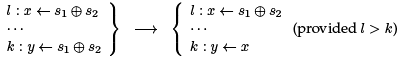
It was suggested in lecture that this optimization would be correct even if the binary operator is effectful. The reason is that if l dominates k then we always execute l first. If the operation does not raise an exception, then the use of x in k is correct. If it does raise an exception, we never reach k. So, yes, this optimization works even for binary operations that may potentially raise an exception.
➤ Dominance
On general control flow graphs, dominance is an interesting relation and there are several algorithms for computing this relationship. We can cast it as a form of forward data-flow analysis. One of the approaches exploits the simplicity of our language to directly generate the dominance relationship as part of code generation. We briefly discuss this here. The drawback is that if your code generation is slightly different or more efficient, or if your transformation change the essential structure of the control flow graph, then you need to update the relationship. A simple and fast algorithm that works particularly well in our simple language is described by Cooper et al. [CHK06] which is empirically faster than the traditional Lengauer-Tarjan algorithm [LT79] (which is asymptotically faster). In this lecture, we consider just the basic cases.
For straight-line code the predecessor if each line is its immediate dominator, and any preceding line is a dominator.
For conditionals, consider if (e; s1 ; s2 )
We translate this to the following code,  is the code for e and s, respectively and e^ is the temp through which we can refer to the result of evaluating e.
is the code for e and s, respectively and e^ is the temp through which we can refer to the result of evaluating e.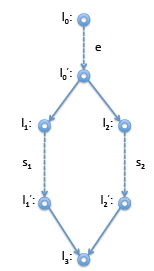
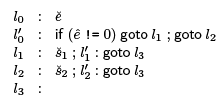
On the right is the corresponding control-flow graph. Now the immediate dominator of l1 should be l'0 and the immediate dominator of l2 should also be l'0 . Now for l3 we don’t know if we arrive from l'0 or from l'2. Therefore, neither of these nodes will dominate l3. Instead, the immediate dominator is l'0 , the last node we can be sure to be traversed before we arrive at l'3 . Indicating immediate dominators with dashed read lines, we show the result below.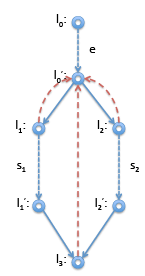 However, if it turns out, say, l'1 is not reachable, then the dominator relationship looks different. This is the case, for example, if s1 in this example is a return statement or is known to raise an error. Then we have instead:
However, if it turns out, say, l'1 is not reachable, then the dominator relationship looks different. This is the case, for example, if s1 in this example is a return statement or is known to raise an error. Then we have instead: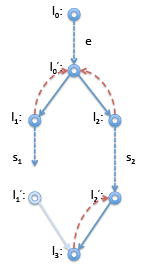 In this case, l'1 : goto l3 is unreachable code and can be optimized away. Of course, the case where l'2 is unreachable is symmetric.
In this case, l'1 : goto l3 is unreachable code and can be optimized away. Of course, the case where l'2 is unreachable is symmetric.
For loops, it is pretty easy to see that the beginning of the loop dominates all the statements in the loop. Again, considering the straightforward compilation of a while loop with the control flow graph on the right.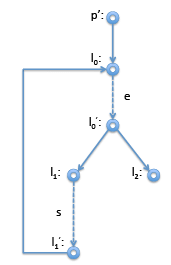
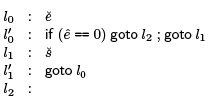
Interesting here is mainly that the node p' just before the loop header l0 is indeed the immediate dominator of l0, even l0 has l'1 as another predecessor. The definition makes this obvious: when we enter the loop we have to come through p' node, on subsequent iterations we come from l'1 . So we cannot be guaranteed to come through l'1 , but we are guaranteed to come through p' on our way to l0.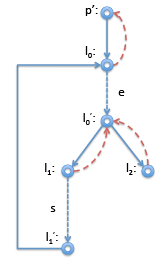 ➤ Implementing Common Subexpression Elimination
➤ Implementing Common Subexpression Elimination
To implement common subexpression elimination we traverse the program, looking for definitions l : x ←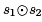 . If
. If 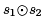 is already in the table, defining variable y at k, we replace l with l : x ← y if k dominates l. Otherwise, we add the expression, line, and variable to the hash table.
is already in the table, defining variable y at k, we replace l with l : x ← y if k dominates l. Otherwise, we add the expression, line, and variable to the hash table.
Dominance can usually be checked quite quickly if we maintain a dominator tree, where each line has a pointer to its immediate dominator. We just follow these pointers until we either reach k (and so k > l) or the root of the control-flow graph (in which case k does not dominate l).
➤ Memory Optimization
Even on modern architectures with hierarchical memory caches, memory access, on average, is still significantly more expensive than register access or even most arithmetic operations. Therefore, memory optimizations play a significant role in generating fast code. As we will see, whether certain memory optimizations are possible or not depends on properties of the whole language. For example, whether or not we can obtain pointers to the middle of heap-allocated objects will be a crucial question to answer.
We will use a simple running example to illustrate applying common subexpression elimination to memory reads. In this example, mult(A; p; q) will multiply matrix A with vector p and return the result in vector q.
Below is the translation into abstract assembly, with the small twist that we have allowed memory reference to be of the form M [base + offset ]. The memory optimization question we investigate is whether some load instructions t ← M [s] can be avoided because the corresponding value is already held in a temp.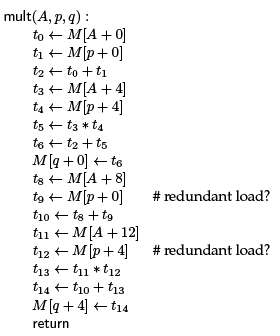
We see that the source refers to p->x and p->y twice, and those are reflected in the two, potentially redundant loads above. Before you read on, consider if we could replace the lines with t9 ← t1 and t12 ← t4. We can do that if we can be assured that memory at the addresses p + 0 and p + 4, respectively, has not changed since the previous load instructions.
It turns out that in C0 the second load is definitely redundant, but the first one may not be.
The first load is not redundant because when this function is called, the pointers p and q might be the same (they might aliased). When this is the case, the store to M [q +0] will likely change the value stored at M [p+0], leading to a different answer than expected for the second line.
On the other hand, this cannot happen for the first line, because M [q + 0] could never be the same as M [p + 4] since one accesses the x field and the other the y field of a struct.
Of course, the answer is mostly likely wrong when p = q. One could either rewrite the code, or require that p = q in the precondition to the function.
In C, the question is more delicate because the use of the address-of (&) operator could obtain pointers to the middle of objects. For example, the argument int[] A would be int* A in C, and such a pointer might have been obtained with &q->x.
➤ Using the Results of Alias Analysis
In C0, the types of pointers are a powerful basis of alias analysis. The way alias analysis is usually phrased is as a may-alias analysis, because we try to infer which pointers in a program may alias. Then we know for optimization purposes that if two pointers are not in the may-alias relationship that they must be different. Writing to one address cannot change the value stored at the other.
Let’s consider how we might use the results of alias analysis, embodied in a predicate may-alias(a; b) for two addresses a and b. We assume we have a load instruction
l : t ← M [a]
and we want to infer if this is available at some other line l' : t' ← M [a] so we could replace it with l' : t0 ← t. Our optimization rule has the same form as previous instances of common subexpression elimination: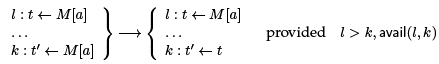
The fact that l dominates k is sufficient here in SSA form to guarantee that the meaning of t and a remains unchanged. avail is supposed to check that M [a] also remains unchanged.
Reaching analysis for memory references is a simple forward dataflow analysis.
If we have a node with two or more incoming control flow edges, it must be available along all of them. For the purposes of traversing loops we assume availability, essentially trying to find a counterexample in the loop. To express this concisely, our analysis rules propagate unavailability of a definition l : t ← M [a] an other instructions k that are dominated by l.
For unavailability, unavail(l; k), we have the seeding rule on the left and the general propagation rule on the right. Because we are in SSA, we know in the seeding rule that l > k where k is the (unique) successor of l'.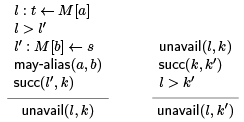
The rule on the right includes the cases of jumps or conditional jumps. This ensures that in a node with multiple predecessors, if a value is unavailable in just one of them, in will be unavailable at the node. Function calls can also seed unavailability.
Unfortunately it is enough if one of the function parameters is a memory reference, because from one memory reference we may be able to get to another by following pointers and offsets.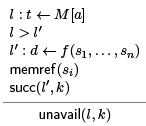
With more information on the shape of memory this rule can be relaxed.
From unavailability we can deduce which memory values are still available, namely those that are not unavailable (restriction attention to those that are dominated by the load—otherwise the question is not asked).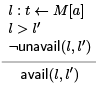
Note that stratification is required: we need to saturate unavail(l; l') before applying this rule.
➤ Type-Based Alias Analysis
The simplest form of alias analysis is based on the type and offset of the address. We call this an alias class, with the idea that pointers in different alias classes cannot
alias. The basic predicate here is class(a; τ ; offset ) which expresses that a is an address derived from a source of type τ and offset offset from the start of the memory of type τ .
Then the may-alias relation is defined by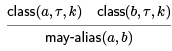
There is a couple of special cases we do not treat explicitly. For example, the location of the array length (which is stored in safe mode at least) may be at offset -8. But such a location can never be written to (array lengths never change, once allocated), so a load of the array length is available at all locations dominated by the load.
The seed of the class relation comes from the compiler, that annotates an address with this information. In our example,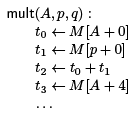
the compiler would generate
class(A; int[ ]; 0)
class(p; struct point*; 0)
class(q; struct point*; 0)
We now propagate the information through a forward dataflow analysis. For example: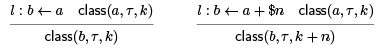
In the second case we have written $n to emphasize the second summand is a constant n. Unfortunately, if it is a variable, we cannot precisely calculate the offset.
This may happen with arrays, but not with pointers, including pointers to structs.
So we need to generalize the third argument to class to be either a variable or T, which indicates any value may be possible. We then have, for example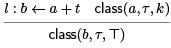
Now T behaves like an information sink. For example, T + k = k + T = T. Since in SSA form a is defined only once, we should not have to change our mind about the class assigned to a variable. However, at parameterized jump targets (which is equivalent to T-functions), we need to “disjoin” the information so that if the argument is known to be k at one predecessor but unknown at T at another predecessor, the result should be T.
Because of loops, we then need to generalize further and introduce ⊥ which means that we believe (for now) that the variable is never used. Because of the seeding by the compiler, this will mostly happen for loop variables. The values are arranged in a lattice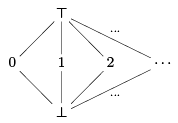
where at the bottom we have more information, at the top the least. The ∪ operation between lattice elements finds the least upper bounds of its two arguments.
For example, 0 ∪ 4 = T and ⊥ ∪ 2 = 2. We use it in SSA form to combine information about offsets. We now read an assertion class(a; τ ; k) as saying that the offset is at least k under the lattice ordering. Then we have Because of loops we might perform this calculation multiple times until we have reached a fixed point. In this case the fixed point is least upper bound of all the offset classes we compute, which is a little different than the saturated data base we considered before.
Because of loops we might perform this calculation multiple times until we have reached a fixed point. In this case the fixed point is least upper bound of all the offset classes we compute, which is a little different than the saturated data base we considered before.
This is an example of abstract interpretation, which may be a subject of a future lecture. One can obtain a more precise alias analysis if one refines the abstract domain, which is lattice shown above.
➤ Allocation-Based Alias Analysis
Another technique to infer that pointers may not alias is based on their allocation point. In brief, if two pointers are allocated with different calls to alloc or alloc array, then they cannot be aliased. Because allocation may happen in a different function than we are currently compiling (and hopefully optimizing), this is an example of an inter-procedural analysis.
|
28 videos|86 docs|31 tests
|
FAQs on Common Subexpression Elimination - Compiler Design - Computer Science Engineering (CSE)
| 1. What is common subexpression elimination in computer science engineering? |  |
| 2. How does common subexpression elimination work? |  |
| 3. What are the benefits of common subexpression elimination? |  |
| 4. Are there any limitations or drawbacks to common subexpression elimination? |  |
| 5. How is common subexpression elimination implemented in compilers? |  |





















