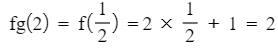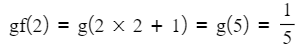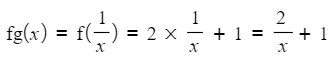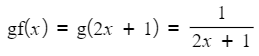Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Composite & Inverse Functions
Composite & Inverse Functions | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Composite Functions
What are Composite Functions?
- A composite function involves applying one function to the output of another function. In simpler terms, it's like performing one operation after another.
- Another term for composite functions is compound functions.
What do composite functions look like?
- Composite function notation is written as fg(x).
- This can be written as f(g(x)) and means “ f applied to the output of g(x)”.
- In this case, g(x) happens first.
- Always apply the outer function to the output of the inner function.
- gf(x) means g(f(x)) and means “g applied to the output of f(x)”.
- In this case, f(x) happens first.
How does a composite function work?
- If you are putting a number into fg(x)
- STEP 1: Put the number into g(x)
- STEP 2: Put the output of g(x) into f(x)
- For example,
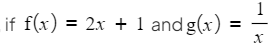
- If you are using algebra, to find an expression for a composite function
- STEP 1: For fg(x) put g(x) wherever you see x in f(x)
- STEP 2: Simplify if necessary
- For example, if
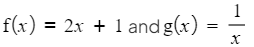
Inverse Functions
What is an inverse function?
- An inverse function performs the opposite operation of the original function. For instance, if the initial function "doubles the number and adds 1," the inverse function would "subtract 1 and halve the result." It essentially reverses the operations in the opposite order.
- Inverse functions essentially undo the actions of the original function.
How do I write inverse functions?
- An inverse function f-1 can be written as
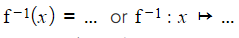
- For example, if f(x) = 2x + 1 its inverse can be written as
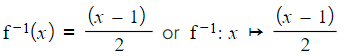
How do I find an inverse function?
- The easiest way to find an inverse function is to 'cheat' and swap the x and y variables.
- Note: This is useful here but should not be done in other math contexts.
- Step-by-Step Process:
- STEP 1: Write the function in the form y = …
- STEP 2: Swap the 𝑥x and 𝑦y to get x = …
- STEP 3: Rearrange the expression to make 𝑦y the subject again
- STEP 4: Write as f−1(x) = … (or f−1 : x↦…)
- Ensure 𝑦y does not exist in the final answer
- Example:
- Given f(x) = 2x + 1, find its inverse:
- STEP 1: Write the function as y = 2x + 1
- STEP 2: Swap x and y: x = 2y + 1
- STEP 3: Rearrange to make y the subject:
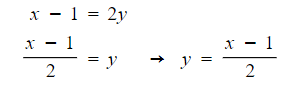
- STEP 4: Write the inverse function:
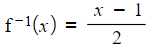
How does a function relate to its inverse?
- If f(3) = 10, then the input of 3 gives an output of 10.
- The inverse function undoes f(x).
- An input of 10 into the inverse function gives an output of 3.
- Therefore, if f(3) = 10, then f−1 (10) = 3.
- The relationship between a function and its inverse is:
- f(f −1 (x)) = f −1 (f(x)) = x
- Applying a function to x, then immediately applying its inverse function, returns x.
- f and f−1 cancel each other out when applied together.
- If f(x) = 2x and you want to solve f−1 (x) = 5:
- Finding the inverse function f −1 (x) directly is difficult without knowledge of logarithms.
- Instead, take f of both sides and use the fact that f and f−1 cancel each other out:
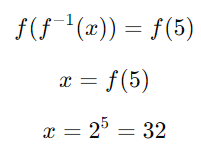
How do I find the domain and range of an inverse function?
- The domain of an inverse function is the same as the range of the original function
- The range of an inverse function is the same as the domain of the original function
The document Composite & Inverse Functions | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
Related Searches