Probability: Solved Examples- 2 | CSAT Preparation - UPSC PDF Download
Example 1: An urn contains 10 white and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that first is white and second is black?
Solution: Let A = Getting a white ball in the first draw B = Getting a Black Ball in the second draw. Required Probability = Probability of getting a white ball in the first draw and a black ball in second draw = P(A and B) = P (A ∩B) = P (A) .P(B/A)
P(A) = (10C1/25C1) = (10/25) = (2/5) and P(B/A) = Probability of getting a black ball in the second draw
when a white ball has already been in first draw = (15C1/24C1) = (15/24) = (5/8)
⇒ Required probability 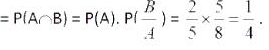
Example3: Hunar wrote two sections of CAT paper ; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?
Using the law of total probability P(golden crystal) = P(A) = P(E1) . 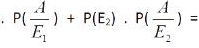
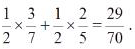
Then by Law of total probability: P(M) = P (M| L) . P(L) + P (M | NL) . P(NL)
= (2/7).(1/4) + (1/7).(3/4) = 5/28
Then by the Law of total probability:
P(A) = P(A | X)-P(X) + P(A | Y) P(Y ) + P(A/Z).P(Z).
= (4/ 10).(1/ 3) + (1/ 6) . (1/ 3) + (3/8) .(1/3) = 113/360 .
|
207 videos|276 docs|138 tests
|
FAQs on Probability: Solved Examples- 2 - CSAT Preparation - UPSC
| 1. What is probability and how is it calculated? |  |
| 2. How can probability be used in real-life situations? |  |
| 3. What are the different types of probability? |  |
| 4. What is the difference between independent and dependent events in probability? |  |
| 5. How can probability be used to make informed decisions? |  |
















