Computing Definite Integrals | Calculus - Mathematics PDF Download
Computing Definite Integrals
In this section we are going to concentrate on how we actually evaluate definite integrals in practice. To do this we will need the Fundamental Theorem of Calculus, Part II.
Fundamental Theorem of Calculus, Part II
Suppose f(x) is a continuous function on [a,b] and also suppose that F(x) is any anti-derivative for f(x). Then,
Recall that when we talk about an anti-derivative for a function we are really talking about the indefinite integral for the function. So, to evaluate a definite integral the first thing that we’re going to do is evaluate the indefinite integral for the function. This should explain the similarity in the notations for the indefinite and definite integrals.
Also notice that we require the function to be continuous in the interval of integration. This was also a requirement in the definition of the definite integral. We didn’t make a big deal about this in the last section. In this section however, we will need to keep this condition in mind as we do our evaluations.
Next let’s address the fact that we can use any anti-derivative of f(x) in the evaluation.
Let’s take a final look at the following integral.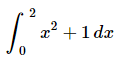
Both of the following are anti-derivatives of the integrand.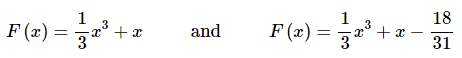
Using the Fundamental Theorem of Calculus to evaluate this integral with the first anti-derivatives gives,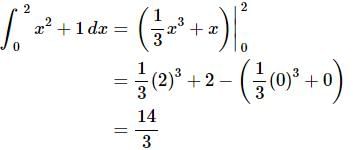
Much easier than using the definition wasn’t it? Let’s now use the second anti-derivative to evaluate this definite integral.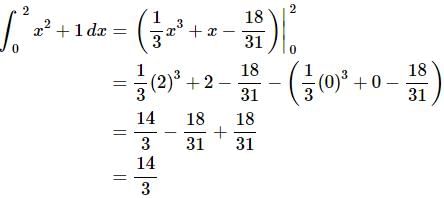
The constant that we tacked onto the second anti-derivative canceled in the evaluation step. So, when choosing the anti-derivative to use in the evaluation process make your life easier and don’t bother with the constant as it will only end up canceling in the long run.
Also, note that we’re going to have to be very careful with minus signs and parenthesis with these problems. It’s very easy to get in a hurry and mess them up.
Let’s start our examples with the following set designed to make a couple of quick points that are very important.
Example 1: Evaluate each of the following.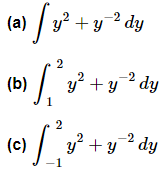
Ans: 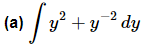
This is the only indefinite integral in this section and by now we should be getting pretty good with these so we won’t spend a lot of time on this part. This is here only to make sure that we understand the difference between an indefinite and a definite integral. The integral is,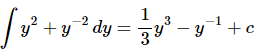
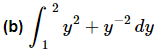
Ans: Recall from our first example above that all we really need here is any anti-derivative of the integrand. We just computed the most general anti-derivative in the first part so we can use that if we want to. However, recall that as we noted above any constants we tack on will just cancel in the long run and so we’ll use the answer from (a) without the “+c”.
Here’s the integral,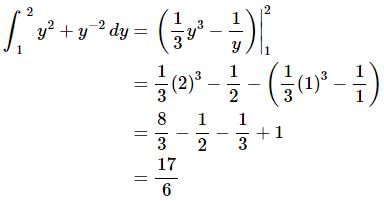
Remember that the evaluation is always done in the order of evaluation at the upper limit minus evaluation at the lower limit. Also, be very careful with minus signs and parenthesis. It’s very easy to forget them or mishandle them and get the wrong answer.
Notice as well that, in order to help with the evaluation, we rewrote the indefinite integral a little. In particular we got rid of the negative exponent on the second term. It’s generally easier to evaluate the term with positive exponents.
Ans: This integral is here to make a point. Recall that in order for us to do an integral the integrand must be continuous in the range of the limits. In this case the second term will have division by zero at y=0 and since y=0 is in the interval of integration, i.e. it is between the lower and upper limit, this integrand is not continuous in the interval of integration and so we can’t do this integral.
Note that this problem will not prevent us from doing the integral in (b) since y=0 is not in the interval of integration.
So, what have we learned from this example?
First, in order to do a definite integral the first thing that we need to do is the indefinite integral. So, we aren’t going to get out of doing indefinite integrals, they will be in every integral that we’ll be doing in the rest of this course so make sure that you’re getting good at computing them.
Second, we need to be on the lookout for functions that aren’t continuous at any point between the limits of integration. Also, it’s important to note that this will only be a problem if the point(s) of discontinuity occur between the limits of integration or at the limits themselves. If the point of discontinuity occurs outside of the limits of integration the integral can still be evaluated.
In the following sets of examples we won’t make too much of an issue with continuity problems, or lack of continuity problems, unless it affects the evaluation of the integral. Do not let this convince you that you don’t need to worry about this idea. It arises often enough that it can cause real problems if you aren’t on the lookout for it.
Finally, note the difference between indefinite and definite integrals. Indefinite integrals are functions while definite integrals are numbers.
Let’s work some more examples.
Example 2: Evaluate each of the following.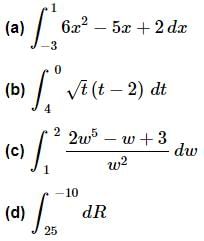
Ans: 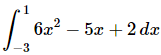
There isn’t a lot to this one other than simply doing the work.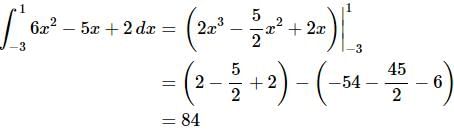
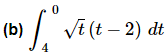
Ans: Recall that we can’t integrate products as a product of integrals and so we first need to multiply the integrand out before integrating, just as we did in the indefinite integral case.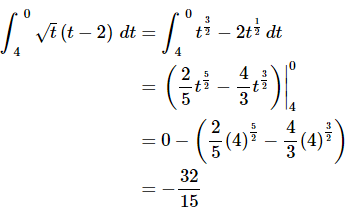
In the evaluation process recall that,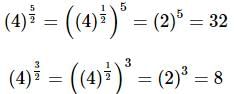
Also, don’t get excited about the fact that the lower limit of integration is larger than the upper limit of integration. That will happen on occasion and there is absolutely nothing wrong with this.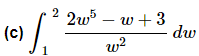
Ans: First, notice that we will have a division by zero issue at w=0, but since this isn’t in the interval of integration we won’t have to worry about it.
Next again recall that we can’t integrate quotients as a quotient of integrals and so the first step that we’ll need to do is break up the quotient so we can integrate the function.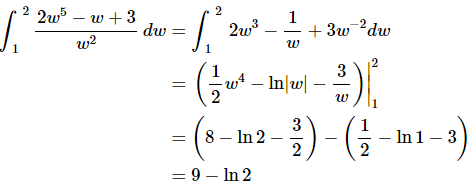
Don’t get excited about answers that don’t come down to a simple integer or fraction. Often times they won’t. Also, don’t forget that ln(1)=0.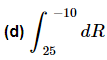
Ans: This one is actually pretty easy. Recall that we’re just integrating 1.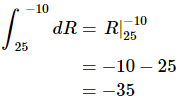
The last set of examples dealt exclusively with integrating powers of x. Let’s work a couple of examples that involve other functions.
Example 3: Problem Statement.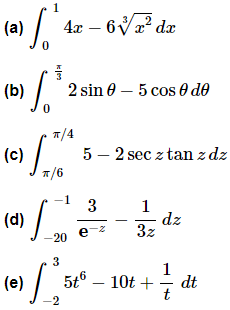
Ans: 
This one is here mostly here to contrast with the next example.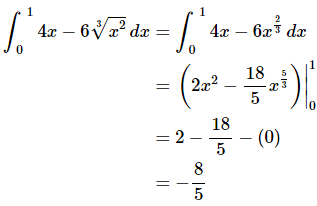
Ans: Be careful with signs with this one. Recall from the indefinite integral sections that it’s easy to mess up the signs when integrating sine and cosine.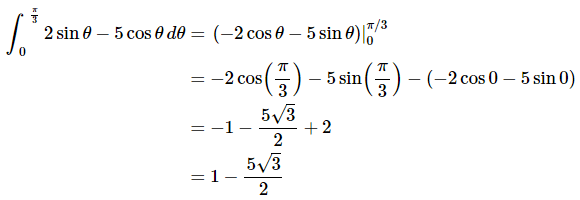
Compare this answer to the previous answer, especially the evaluation at zero. It’s very easy to get into the habit of just writing down zero when evaluating a function at zero. This is especially a problem when many of the functions that we integrate involve only x’s raised to positive integers; these evaluate is zero of course. After evaluating many of these kinds of definite integrals it’s easy to get into the habit of just writing down zero when you evaluate at zero. However, there are many functions out there that aren’t zero when evaluated at zero so be careful.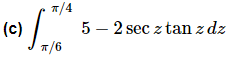
Ans: Not much to do other than do the integral.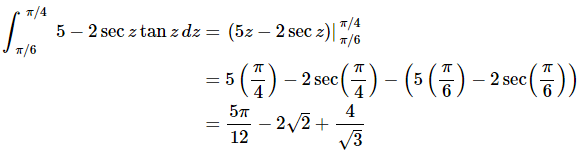
For the evaluation, recall that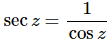
and so if we can evaluate cosine at these angles we can evaluate secant at these angles.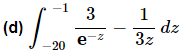
Ans: In order to do this one will need to rewrite both of the terms in the integral a little as follows,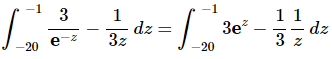
For the first term recall we used the following fact about exponents.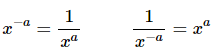
In the second term, taking the 3 out of the denominator will just make integrating that term easier.
Now the integral.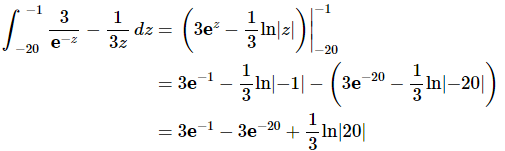
Just leave the answer like this. It’s messy, but it’s also exact.
Note that the absolute value bars on the logarithm are required here. Without them we couldn’t have done the evaluation.
Ans: This integral can’t be done. There is division by zero in the third term at t=0 and t=0 lies in the interval of integration. The fact that the first two terms can be integrated doesn’t matter. If even one term in the integral can’t be integrated then the whole integral can’t be done.
So, we’ve computed a fair number of definite integrals at this point. Remember that the vast majority of the work in computing them is first finding the indefinite integral. Once we’ve found that the rest is just some number crunching.
There are a couple of particularly tricky definite integrals that we need to take a look at next. Actually they are only tricky until you see how to do them, so don’t get too excited about them. The first one involves integrating a piecewise function.
Example 4: Given,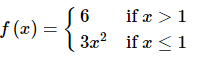
Evaluate each of the following integrals.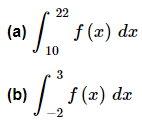
Ans: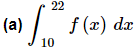
For this integral notice that x=1 is not in the interval of integration and so that is something that we’ll not need to worry about in this part.
Also note the limits for the integral lie entirely in the range for the first function. What this means for us is that when we do the integral all we need to do is plug in the first function into the integral.
Here is the integral.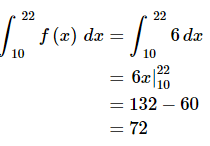
Ans: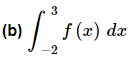
In this part x=1 is between the limits of integration. This means that the integrand is no longer continuous in the interval of integration and that is a show stopper as far we’re concerned. As noted above we simply can’t integrate functions that aren’t continuous in the interval of integration.Also, even if the function was continuous at x=1x=1 we would still have the problem that the function is actually two different equations depending where we are in the interval of integration.Let’s first address the problem of the function not being continuous at x=1. As we’ll see, in this case, if we can find a way around this problem the second problem will also get taken care of at the same time.In the previous examples where we had functions that weren’t continuous we had division by zero and no matter how hard we try we can’t get rid of that problem. Division by zero is a real problem and we can’t really avoid it. In this case the discontinuity does not stem from problems with the function not existing at x=1. Instead the function is not continuous because it takes on different values on either sides of x=1. We can “remove” this problem by recalling Property 5 from the previous section. This property tells us that we can write the integral as follows,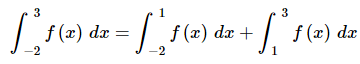
On each of these intervals the function is continuous. In fact we can say more. In the first integral we will have xx between -2 and 1 and this means that we can use the second equation for f(x) and likewise for the second integral x will be between 1 and 3 and so we can use the first function for f(x). The integral in this case is then,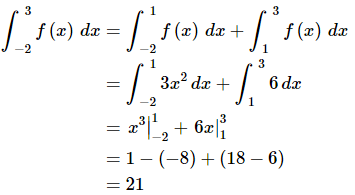
So, to integrate a piecewise function, all we need to do is break up the integral at the break point(s) that happen to occur in the interval of integration and then integrate each piece.
Next, we need to look at is how to integrate an absolute value function.
Example 5: Evaluate the following integral.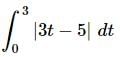
Ans: Recall that the point behind indefinite integration (which we’ll need to do in this problem) is to determine what function we differentiated to get the integrand. To this point we’ve not seen any functions that will differentiate to get an absolute value nor will we ever see a function that will differentiate to get an absolute value.
The only way that we can do this problem is to get rid of the absolute value. To do this we need to recall the definition of absolute value.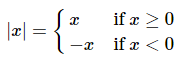
Once we remember that we can define absolute value as a piecewise function we can use the work from Example 4 as a guide for doing this integral.
What we need to do is determine where the quantity on the inside of the absolute value bars is negative and where it is positive. It looks like if 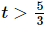 the quantity inside the absolute value is positive and if
the quantity inside the absolute value is positive and if 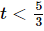 the quantity inside the absolute value is negative.
the quantity inside the absolute value is negative.
Next, note that 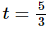 is in the interval of integration and so, if we break up the integral at this point we get,
is in the interval of integration and so, if we break up the integral at this point we get,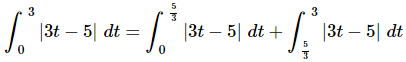
Now, in the first integrals we have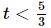 and so 3t - 5 < 0 in this interval of integration. That means we can drop the absolute value bars if we put in a minus sign. Likewise, in the second integral we have
and so 3t - 5 < 0 in this interval of integration. That means we can drop the absolute value bars if we put in a minus sign. Likewise, in the second integral we have  which means that in this interval of integration we have 3t - 5 > 0 and so we can just drop the absolute value bars in this integral.
which means that in this interval of integration we have 3t - 5 > 0 and so we can just drop the absolute value bars in this integral.
After getting rid of the absolute value bars in each integral we can do each integral. So, doing the integration gives,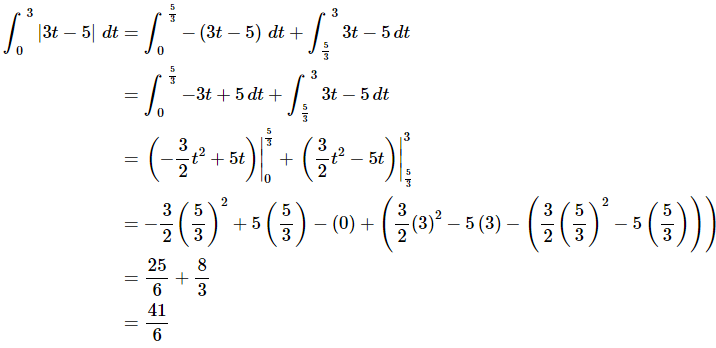
Integrating absolute value functions isn’t too bad. It’s a little more work than the “standard” definite integral, but it’s not really all that much more work. First, determine where the quantity inside the absolute value bars is negative and where it is positive. When we’ve determined that point all we need to do is break up the integral so that in each range of limits the quantity inside the absolute value bars is always positive or always negative. Once this is done we can drop the absolute value bars (adding negative signs when the quantity is negative) and then we can do the integral as we’ve always done.
Even and Odd Functions
This is the last topic that we need to discuss in this section.
First, recall that an even function is any function which satisfies,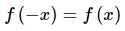
Typical examples of even functions are,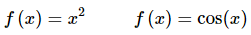
An odd function is any function which satisfies,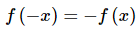
The typical examples of odd functions are,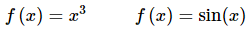
There are a couple of nice facts about integrating even and odd functions over the interval [-a,a]. If f (x) is an even function then,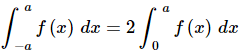
Likewise, if f(x) is an odd function then,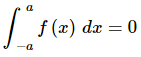
Note that in order to use these facts the limit of integration must be the same number, but opposite signs!
Example 6: Integrate each of the following.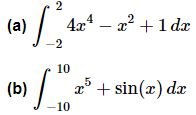
Neither of these are terribly difficult integrals, but we can use the facts on them anyway.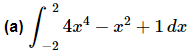
Ans:
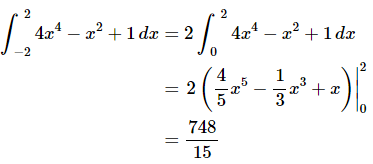
So, using the fact cut the evaluation in half (in essence since one of the new limits was zero).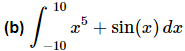
Ans: The integrand in this case is odd and the interval is in the correct form and so we don’t even need to integrate. Just use the fact.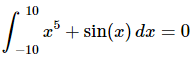
Note that the limits of integration are important here. Take the last integral as an example. A small change to the limits will not give us zero.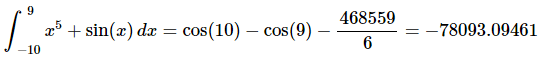
The moral here is to be careful and not misuse these facts.
Pratice problems: Computing Definite Integrals
Q.1. Evaluate each of the following integrals.
Ans:This is just an indefinite integral and by this point we should be comfortable doing them so here is the answer to this part.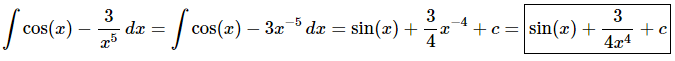
Don’t forget to add on the “+c” since we are doing an indefinite integral!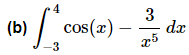
Ans: Recall that in order to do a definite integral the integrand (i.e. the function we are integrating) must be continuous on the interval over which we are integrating, [3,4]
in this case. We can clearly see that the second term will have division by zero at x= 0 and x = 0 is in the interval over which we are integrating and so this function is not continuous on the interval over which we are integrating.
Therefore, this integral cannot be done.
Ans: Now, the function still has a division by zero problem in the second term at x= 0 However, unlike the previous part x=0 does not fall in the interval over which we are integrating, [1,4] in this case.
This integral can therefore be done. Here is the work for this integral.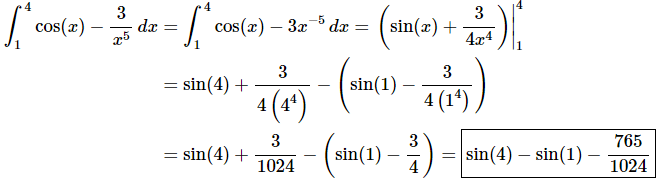
Q.2. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.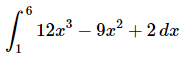
Ans: First we need to integrate the function.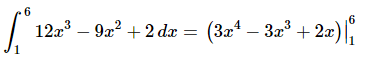
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.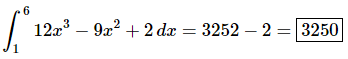
Q.3. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.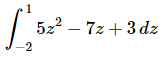
Ans: First we need to integrate the function.
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.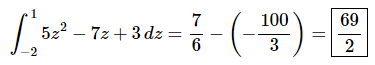
Q.4. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.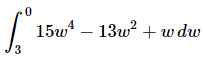
Ans: First, do not get excited about the fact that the lower limit of integration is a larger number than the upper limit of integration. The problem works in exactly the same way.
So, we need to integrate the function.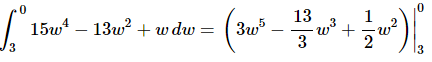
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.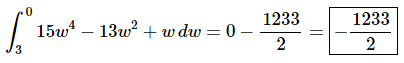
Q.5. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.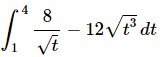
Ans: First we need to integrate the function.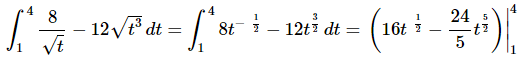
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.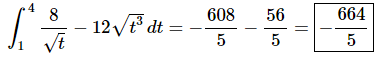
Q.6. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.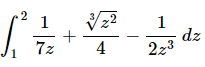
Ans: First we need to integrate the function.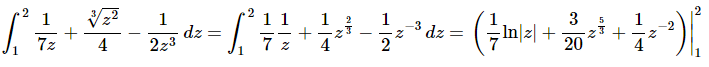
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.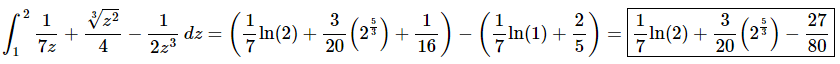
Don’t forget that ln(1)=0! Also, don’t get excited about “messy” answers like this. They happen on occasion.
Q.7. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.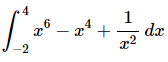
Ans: In this case note that the third term will have division by zero at x=0 and this is in the interval we are integrating over, [−2,4] and hence is not continuous on this interval.
Therefore, this integral cannot be done
Q.8. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.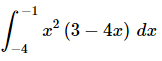
Ans: In this case we’ll first need to multiply out the integrand before we actually do the integration. Doing that integrating the function gives,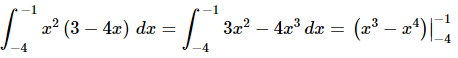
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.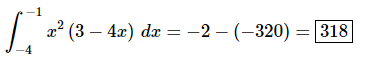
Q.9. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.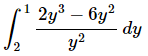
Ans: In this case we’ll first need to simplify the integrand to remove the quotient before we actually do the integration. Doing that integrating the function gives,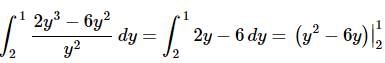
Do not get excited about the fact that the lower limit of integration is larger than the upper limit of integration. This will happen on occasion and the integral works in exactly the same manner as we’ve been doing them.
Also, recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.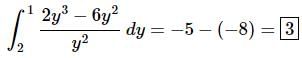
Q.10. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.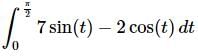
Ans: First we need to integrate the function.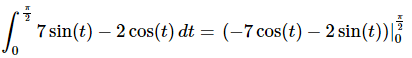
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.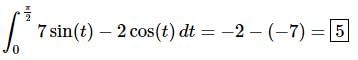
Q.11. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.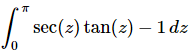
Ans: Be careful with this integral. Recall that,
Also recall that 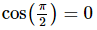 and that
and that 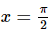 is in the interval we are integrating over,
is in the interval we are integrating over,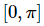 and hence is not continuous on this interval.
and hence is not continuous on this interval.
Therefore, this integral cannot be done.
It is often easy to overlook these kinds of division by zero problems in integrands when the integrand is not explicitly written as a rational expression. So, be careful and don’t forget that division by zero can sometimes be “hidden” in the integrand!
Q.12. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.
Ans: First notice that even though we do have some “hidden” rational expression here (in the definitions of the trig functions) neither cosine nor sine is zero in the interval we are integrating over and so both terms are continuous over the interval.
Therefore all we need to do integrate the function.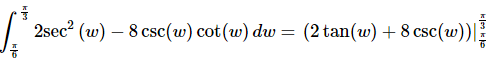
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.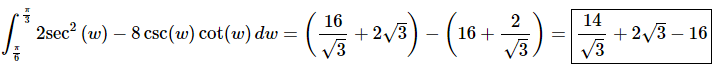
Q.13. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.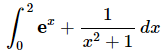
Ans: First we need to integrate the function.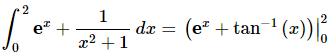
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.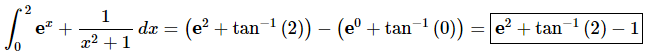
Note that tan-1 (0)=0 but tan-1 (2) doesn’t have a “nice” answer and so was left as is.
Q.14. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.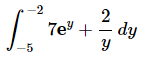
Ans: First we need to integrate the function.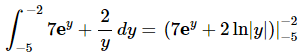
Recall that we don’t need to add the “+c” in the definite integral case as it will just cancel in the next step.
The final step is then just to do the evaluation.
We’ll leave the basic arithmetic to you to verify and only show the results of the evaluation. Make sure that you evaluate the upper limit first and then subtract off the evaluation at the lower limit.
Here is the answer for this problem.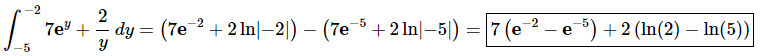
Q.15. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.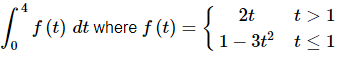
Ans: This integral can’t be done as a single integral give the obvious change of the function at t=1 which is in the interval over which we are integrating. However, recall that we can always break up an integral at any point and t=1 seems to be a good point to do this.Breaking up the integral at t=1 gives,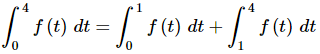
So, in the first integral we have 0 ≤ t ≤ 1 and so we can use f (t)=1−3t2 in the first integral. Likewise, in the second integral we have 1 ≤ t ≤ 4 and so we can use f (t)=2t in the second integral.
Making these function substitutions gives,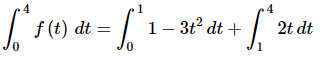
All we need to do at this point is evaluate each integral. Here is that work.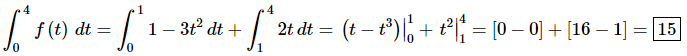
Q.16. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.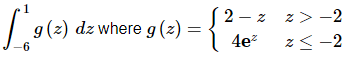
Ans: This integral can’t be done as a single integral give the obvious change of the function at z=−2 which is in the interval over which we are integrating. However, recall that we can always break up an integral at any point and z=−2 seems to be a good point to do this.
Breaking up the integral at z=−2 gives,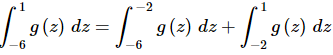
All we need to do at this point is evaluate each integral. Here is that work.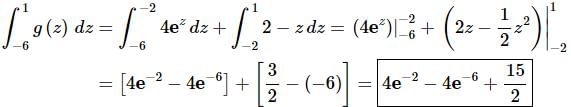
Q.17. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.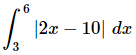
Ans: We’ll need to “remove” the absolute value bars in order to do this integral. However, in order to do that we’ll need to know where 2x−10 is positive and negative.
Since 2x−10 is the equation of a line is should be fairly clear that we have the following positive/negative nature of the function.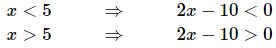
So, to remove the absolute value bars all we need to do then is break the integral up at x=5.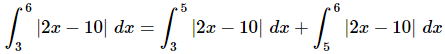 |
|
So, in the first integral we have 3 ≤ x≤ 5 and so we have |2x−10|=−(2x−10) in the first integral. Likewise, in the second integral we have 5≤x≤6 and so we have |2x−10|=2x−10 in the second integral. Or,
All we need to do at this point is evaluate each integral. Here is that work.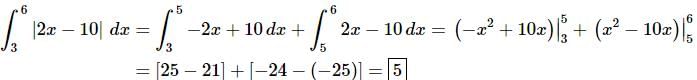
Q.18. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.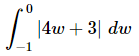
Ans: We’ll need to “remove” the absolute value bars in order to do this integral. However, in order to do that we’ll need to know where 4w+34 is positive and negative.
Since 4w+3 is the equation a line is should be fairly clear that we have the following positive/negative nature of the function.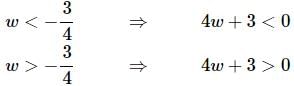
So, to remove the absolute value bars all we need to do then is break the integral up at 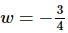
So, in the first integral we have 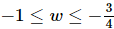 and so we have |4w+3|=−(4w+3) in the first integral. Likewise, in the second integral we have
and so we have |4w+3|=−(4w+3) in the first integral. Likewise, in the second integral we have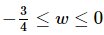 and so we have |4w+3|=4w+3 in the second integral. Or,
and so we have |4w+3|=4w+3 in the second integral. Or,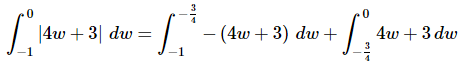
All we need to do at this point is evaluate each integral. Here is that work.
|
112 videos|65 docs|3 tests
|
FAQs on Computing Definite Integrals - Calculus - Mathematics
| 1. What is a definite integral? |  |
| 2. How do you compute a definite integral? |  |
| 3. What are the main properties of definite integrals? |  |
| 4. Can definite integrals be negative? |  |
| 5. What is the significance of definite integrals in real-life applications? |  |





















