Conditional Probability and its Properties | Mathematics (Maths) for JEE Main & Advanced PDF Download
Conditional Probability and Multiplication Theorem
Let A and B be two events such that P(A) > 0. Then P(B|A) denote the conditional probability of B given that A has occurred. Since A is known to have occurred, it becomes the new sample space replacing the original S. From this we led to the definition. which is called conditional probability of B given A.
⇒ 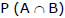 = P(A) P(B | A) which is called compound probability or multiplication theorem. It says the probability that both A and B occur is equal to the probability that A occur times the probability that B occurs given that A has occurred.
= P(A) P(B | A) which is called compound probability or multiplication theorem. It says the probability that both A and B occur is equal to the probability that A occur times the probability that B occurs given that A has occurred.
Note : For any three events A1, A2, A3 we have 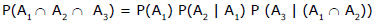
Ex.1 Two dice are thrown. Find the probability that the numbers appeared has a sum of 8 if it is known that the second dice always exhibits 4.
Sol. Let A be the event of occurrence of 4 always on the second die
= {(1,4), (2, 4), (3, 4) (4,4), (5, 4), (6, 4)} ;
 n(A) = 6
n(A) = 6
and B be the event of occurrence of such numbers on both dice whose sum is 8 = {(4, 4)}.
Thus, A ∩ B = A ∩ {(4, 4)} = {(4, 4)}
 n(A Ç B) = 1
n(A Ç B) = 1
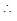
Ex.2 A bag contains 3 red, 6 white and 7 blue balls. Two balls are drawn one by one. What is the probability that first ball is white and second ball is blue when first drawn ball is not replaced in the bag ?
Sol. Let A be the event of drawing first ball white and B be the event of drawing second ball blue.
Here A and B are dependent events.
P(A) = , P (B|A) =
⇒ P(AB) = P(A). P(B/A) =
Ex.3:A bag contains 4 red and 4 blue balls. Four balls are drawn one by one from the bag, then find the probability that the drawn balls are in alternate colour.
Sol. E1 : Event that first drawn ball is red, second is blue and so on.
E2 : Event that first drawn ball is blue, second is red and so on.
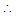 P(E1) =
P(E1) = and
P(E2) =
⇒ P(E) = P(E1) + P(E2) =
Ex 4: In a survey in a class, the probability for a person to watch videos is 0.8 and the probability for a person to be a topper, if given that he watches videos is 0.99. find the probability for a person to be both topper and watches videos.
Solution:
let Event E denotes the event that a person watches Examfear videos
let Event F denotes the event that a person is topper
then P(E) = the probability that a person watches Examfear videos =0.8
and P(F|E)= the probability that a person is a topper if he watches Examfear videos=0.99
then P (E ∩ F)= the probability that a person is both topper and also watches Examfear videos
then according to Multiplication Theorem on probability
P (E ∩ F) = P (E) P (F | E)
= 0.8 x 0.99
= 0.792
∴ The probability that a person is both topper and also watches videos = 0.792
|
172 videos|476 docs|154 tests
|
FAQs on Conditional Probability and its Properties - Mathematics (Maths) for JEE Main & Advanced
| 1. What is conditional probability? |  |
| 2. What are the properties of conditional probability? |  |
| 3. How is conditional probability calculated? |  |
| 4. Can conditional probability be used to predict future events? |  |
| 5. How is conditional probability applied in real-life scenarios? |  |






















