Conditional Probability | Engineering Mathematics - Civil Engineering (CE) PDF Download

Clear all your Civil Engineering (CE) doubts with EduRev Join for Free

Join for Free

Introduction

Conditional probability P(A | B) indicates the probability of event ‘A’ happening given that event B happened.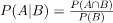
We can easily understand the above formula using the below diagram. Since B has already happened, the sample space reduces to B. So the probability of A happening becomes  divided by P(B)

Example: In a batch, there are 80% C programmers, and 40% are Java and C programmers. What is the probability that a C programmer is also Java programmer?
Solution: Let A → Event that a student is Java programmer
B → Event that a student is C programmer
P(A | B) = P(A ∩ B) / P(B)
= (0.4) / (0.8)
= 0.5
So there are 50% chances that student that knows C also knows Java

Product Rule

Derived from above definition of conditional probability by multiplying both sides with P(B)
P(A ∩ B) = P(B) * P(A | B)

Understanding Conditional probability through tree:
Computation for Conditional Probability can be done using tree, This method is very handy as well as fast when for many problems.

Example: In a certain library, twenty percent of the fiction books are worn and need replacement. Ten percent of the non-fiction books are worn and need replacement. Forty percent of the library’s books are fiction and sixty percent are non-fiction. What is the probability that a book chosen at random are worn? Draw a tree diagram representing the data.
Solution: Let F represents fiction books and N represents non-fiction books. Let W represents worn books and G represents non-worn books.

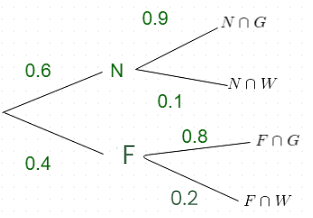
P(worn) = P(N) * P(W | N) + P(F) * P(W | F)
= 0.6 * 0.1 + 0.4 * 0.2
= 0.14