Continuity | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Definition |

|
| One-sided Continuity |

|
| Continuity In An Interval |

|
| Theorems of Continuity |

|
Definition
Continuity at a Point: A function f is continuous at c if the following three conditions are met.
- f(x) is defined.
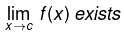
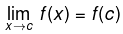
In other words function f(x) is said to be continuous at x = c , if 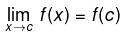
Symbolically f is continuous at x = c

One-sided Continuity
- A function f defined in some neighbourhood of a point c for c ⇒ c is said to be continuous at c from the left if
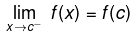
- A function f defined in some neighbourhood of a point c for x ³ c is said to be continuous at c from the right if
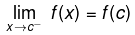
- One-sided continuity is a collective term for functions continuous from the left or from the right.
- If the function f is continuous at c, then it is continuous at c from the left and from the right . Conversely, if the function f is continuous at c from the left and from the right, then
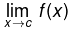 exists &
exists & 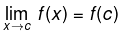
- The last equality means that f is continuous at c.
- If one of the one-sided limits does not exist, then
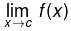 does not exist either. In this case, the point c is a discontinuity in the function, since the continuity condition is not met.
does not exist either. In this case, the point c is a discontinuity in the function, since the continuity condition is not met.
Continuity In An Interval
- A function f is said to be continuous in an open interval (a , b) if f is continuous at each & every point ∈(a, b).
- A function f is said to be continuous in a closed interval [a,b] if:
(i) f is continuous in the open interval (a , b) &
(ii) f is right continuous at `a' i.e.
(iii) f is left continuous at `b' i.e.
A function f can be discontinuous due to any of the following three reasons:
 does not exist i.e.
does not exist i.e. 
- f(x) is not defined at x= c
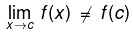
- Geometrically, the graph of the function will exhibit a break at x= c.
Example 1. Test the following functions for continuity
(a) 2x5 - 8x2 + 11 / x4 + 4x3 + 8x2 + 8x +4
(b) f(x) = 3sin3x + cos2x + 1 / 4cos x - 2
Solution.
(a) A function representing a ratio of two continuous functions will be (polynomials in this case) discontinuous only at points for which the denominator zero. But in this case (x4 + 4x3 + 8x2 + 8x + 4) = (x2 + 2x + 2)2 = [(x + 1)2 + 1]2 > 0 (always greater than zero)
Hence f(x) is continuous throughout the entire real line.
(b) The function f(x) suffers discontinuities only at points for which the denominator is equal to zero i.e. 4 cos x - 2 = 0 or cos x = 1/2 ⇒ x = xn = ± π/3 + 2nπ(n=0, ±1, ±2...) Thus the function f(x) is continuous everywhere, except at the point xn.
Example 2.

Find A and B so as to make the function continuous.
Solution. At x = - π/2
- π/2 - h
where h→ 0
Replace x by - π/2+h
where h → 0
So B - A = 2 ...(i)
At x = π/2
Replace x by π/2 - h
Replace x by π/2+h
where h→ 0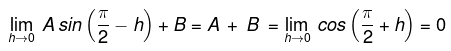
So A+B = 0 ...(ii)
Solving (i) & (ii), B= 1, A = -1
Example 3. Test the continuity of f(x) at x = 0 if
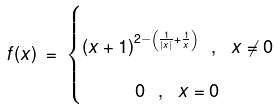
Solution. For x < 0,
L.H.L. = R.H.L. ≠ f(0) Hence f(x) is discontinuous at x = 0.
Example 4. If f(x) be continuous function for all real values of x and satisfies;
x2 + {f(x) – 2} x + 2√3 – 3 – √3 . f(x) = 0, for x ∈ R. Then find the value of f(√3 ).
Solution. As f(x) is continuous for all x ∈ R.
Thus,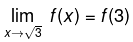
where
f(x) = x2 - 2x + 2√3 - 3 / √3 - x, x ≠ √3
f(√3) = 2(1-√3).
Example 5. 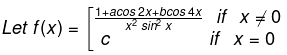
If f (x) is continuous at x = 0, then find the value of (b+c)3-3a.
Solution.
Nr → 1 + a + b Dr → 0
for existence of limit a + b + 1 = 0
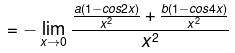
limit of Nr ⇒ 2a+8b = 0 ⇒ a = -4b
hence
-4b+b = -1
⇒ b = 1/3 and a = -4/3
= 8 sin2x - 2 sin22x / 3x4 = 8 sin2x - 8sin2xcos2x / 3x4
= 8 / 3 . sin2x / x2 . sin2x / x2 = 8 / 3
⇒ eA = 1 / 2 (e2x A / x + B / x) ⇒ x . eA = 1 / 2 (e2x . A + B)
Example 6.
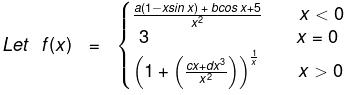
If f is continuous at x = 0, then find the values of a, b, c & d.
Solution.
,
for existence of limit a + b + 5 = 0
= a / 2 + 5 / 2 - a = 3
⇒ a = - 1 ⇒ b = - 4
for existence of limit c = 0
= ed = 3 ⇒ d = ln 3
Example 7. Let f(x) = x3 = 3x2 + 6 ∀ x ∈ R and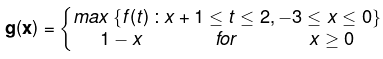
Test continuity of g (x) for x ∈ [-3, 1].
Solution. Since f(x) = x3 - 3x2 + 6 ⇒ f'(x) = 3x2 - 6x = 3x (x - 2) for maxima and minima f'(x) = 0
x = 0, 2
f"(x) = 6x – 6
f" (0) = –6 < 0 (local maxima at x = 0)
f" (2) = 6 > 0 (local minima at x = 2)
x3 – 3x2 + 6 = 0 has maximum 2 positive and 1 negative real roots. f(0) = 6.
Now graph of f(x) is :
Clearly f(x) is increasing in (– ∝, 0) U (2, ∝) and decreasing in (0, 2)
⇒ x + 2 < 0 ⇒ x < – 2 ⇒ –3 ≤ x < – 2
⇒ –2 ≤ x + 1 < –1 and –1 ≤ x + 2 < 0
in both cases f(x) increases (maximum) of g(x) = f(x + 2)
g(x) = f(x + 2); –3 ≤ x < – 2 ...(1)
and if x + 1 < 0 and 0 ≤ x + 2 < 2
– 2 ≤ x < –1 then g(x) = f(0)
Now for x + 1 ≥ 0 and x + 2 < 2 ⇒ –1 ≤ x < 0, g(x) = f(x + 1)
Hence g(x) is continuous in the interval [–3, 1].
Example 8. Given the function,
f(x) = x [ 1 / x(1 + x) + 1 / (1 + x)(1 + 2x) + 1 / (1 + 2x)(1 + 3x) + ....upto ∞
Find f (0) if f (x) is continuous at x = 0.
Solution.
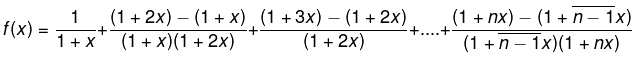
f(x) = 2 / 1 + x - 1 / 1 + nx upto n terms when x ≠0.
Hence 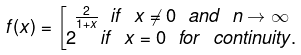
Example 9. Let f: R →R be a function which satisfies f(x+y3) = f(x) + (f(y))3 ∀ x, y ∈ R. If f is continuous at x = 0, prove that f is continuous every where.
Solution.
To prove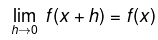
Put x = y = 0 in the given relation f(0) = f(0) + (f(0))3 ⇒ f(0) = 0
Since f is continuous at x = 0
To prove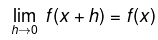
= f(x) + 0 = f(x).
Hence f is continuous for all x ∈ R.
Theorems of Continuity
Theorem 1. If f & g are two functions that are continuous at x= c then the functions defined by F1(x) = f(x) ± g(x) ; F2(x) = K f(x) K any real number ; F3(x) = f(x).g(x) are also continuous at x= c.
Further, if g (c) is not zero, then is also continuous at x = c.
Theorem 2. If f(x) is continuous & g(x) is discontinuous at x = a then the product function ø(x) = f(x) . g(x) is not necessarily discontinuous at x = a .
Theorem 3. If f(x) and g(x) both are discontinuous at x = a then the product function ø(x) = f(x) . g(x) is not necessarily discontinuous at x = a .
Theorem 4: Intermediate Value Theorem
- If f is continuous on the closed interval [a, b] and k is any number between f(a) and f(b), then there is at least one number c in [a, b] such that f(c) = k.
Note:
- The Intermediate Value Theorem tells that at least one c exists, but it does not give a method for finding c. Such theorems are called existence theorems.
- As a simple example of this theorem, consider a person's height. Suppose that a girl is 5 feet tall on her thirteenth birthday and 5 feet 7 inches tall on her fourteenth birthday. Then, for any height h between 5 feet and 7 inches, there must have been a time t when her height was exactly h. This seems reasonable because human growth is continuous and a person's height does not abruptly change from one value to another.
- The Intermediate Value Theorem guarantees the existence of at least one number c in the closed interval [a, b]. There may, of course, be more than one number c such that f(c) = k, as shown in Figure 1. A function that is not continuous does not necessarily possess the intermediate value property. For example, the graph of the function shown in Figure 2 jumps over the horizontal line given by y = k and for this function there is no value of c in [a, b] such that f(c) = k.
- The Intermediate Value Theorem often can be used to locate the zeroes of a function that is continuous on a closed interval. Specifically, if f is continuous on [a, b] and f(a) and f(b) differ in sign, then the intermediate Value Theorem guarantees the existence of at least one zero of f in the closed interval [a, b].


Example 10. Use the Intermediate Value Theorem to show that the polynomial function f(x) = x3 + 2x - 1 has a zero in the interval [0, 1]
Sol. Note that f is continuous on the closed interval [0, 1]. Because
f(0) = 03 + 2(0) - 1 = -1 and f(1) = 13 + 2(1) - 1 = 2
it follows that f(0) < 0 and f(1) > 0. You can therefore apply the Intermediate Value Theorem to conclude that there must be some c in [0, 1] such that f(c) = 0, as shown in Figure 3.
Example 11. State intermediate value theorem and use it to prove that the equation has at least one real root.
Sol. Let f (x) = first, f (x) is continuous on [5, 6]
Hence by intermediate value theorem É at least one value of c ∈ (5, 6) for which f (c) = 0
c is root of the equation
Example 12. If f(x) be a continuous function in then prove that there exists point
Sol.
Let g(x) = f(x) – f(x + π) ....(i)
at x = π; g(π) = f(π) – f(2π) ....(ii)
at x = 0, g(0) = f(0) – f(π) ...(iii)
adding (ii) and (iii), g(0) + g(π) = f(0) – f(2π)
⇒ g(0) + g(π) = 0 [Given f(0) = f(2π) ⇒ g(0) = –g(π)
⇒ g(0) and g(π) are opposite in sign.
⇒ There exists a point c between 0 and p such g(c) = 0 as shown in graph;
From (i) putting x = c g(c) = f(c) – f(c +π) = 0 Hence, f(c) = f(c + π)
|
172 videos|503 docs|154 tests
|
FAQs on Continuity - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of one-sided continuity? |  |
| 2. What does continuity in an interval mean? |  |
| 3. What are some important theorems of continuity? |  |
| 4. How can one determine if a function is continuous at a specific point? |  |
| 5. How can one determine if a function is continuous on a closed interval? |  |
















