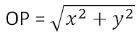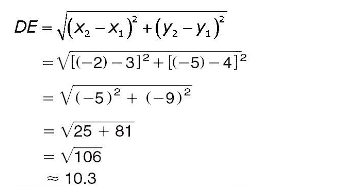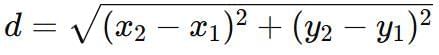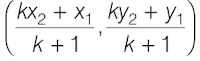Coordinate Geometry Class 10 Notes Maths Chapter 7
What is a Coordinate System?
A Coordinate System is a mathematical framework used to determine the position or location of points in space. It provides a way to describe the position of objects or points using numerical values called coordinates.
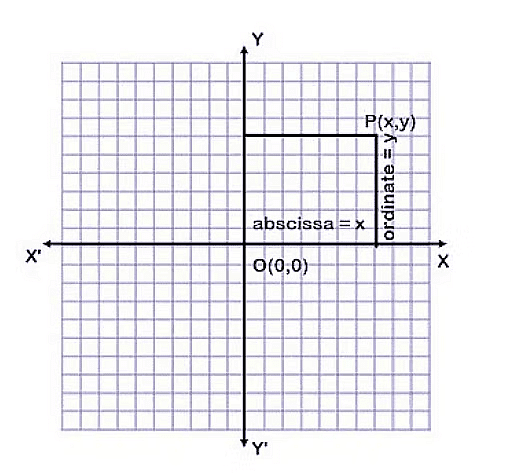
- As shown in the figure, the line XOX′ is known as the X-axis, and YOY′is known as the Y-axis.
- The point O is called the origin. For any point P (x y), the ordered pair(x,y) is called the coordinate of point P.
- The distance of a point from the Y-axis is called its abscissa and the distance of a point from the X-axis is called its ordinate.
Distance Formula
Distance between any two points (x1, y1) and (x2, y2) is given by
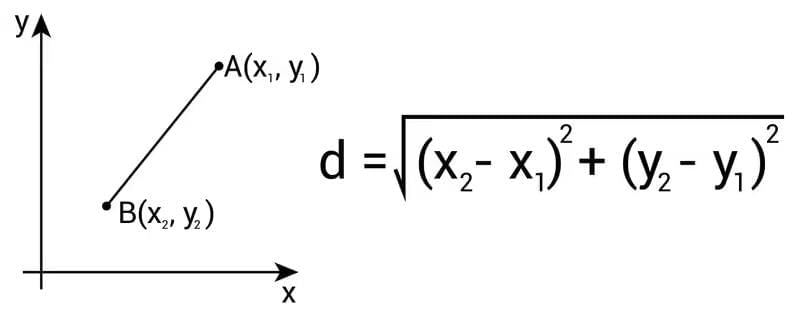
Where d is the distance between the points (x1,y1) and (x2,y2).
Note:The distance of any point P(x,y) from the origin O(0,0) is given by:
Derivation: Distance between Two Points Using Pythagoras' Theorem
Let P(x1, y1) and Q(x2, y2) be any two points on the cartesian plane.
Draw lines parallel to the axes through P and Q to meet at T.
ΔPTQ is right-angled at T.
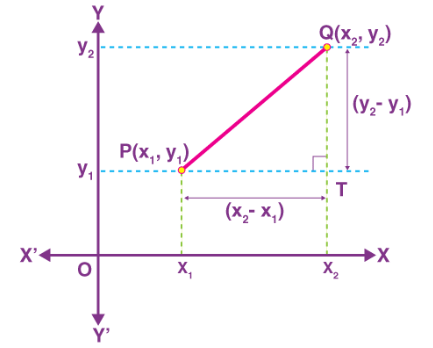
By Pythagoras Theorem,
The distance between two points P (x1, y1) and Q (x2, y2) is given by:
PQ2 = PT2 + QT2
= (x2 – x1)2 + (y2 – y1)2
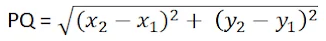
Example 1: Find the distance between the points D and E, in the given figure.
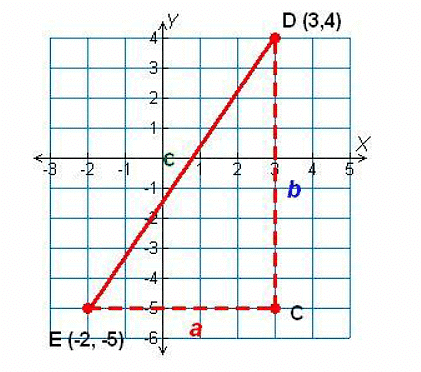
Sol:
Example 2: What is the distance between two points (2, 3) and (-4, 5) using the distance formula?
Sol: The distance formula is used to calculate the distance between two points in a coordinate plane. It is given as:
Using this formula, we can find the distance between the points (2, 3) and (-4, 5) as follows:
d = √[(-4 - 2)² + (5 - 3)²]
d = √[(-6)² + (2)²]
d = √[36 + 4]
d = √40
d = 6.32 (approx.)
Therefore, the distance between the points (2, 3) and (-4, 5) is approximately 6.32 units.
Section Formula
Let P (x,y) be a point on the line segment joining A(x1, y1) and B(x2, y2) such that it divides AB internally in the ratio m:n. The coordinates of the point P are given by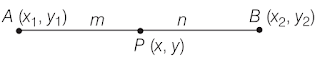
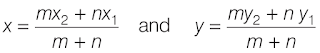
This is known as the Section Formula.
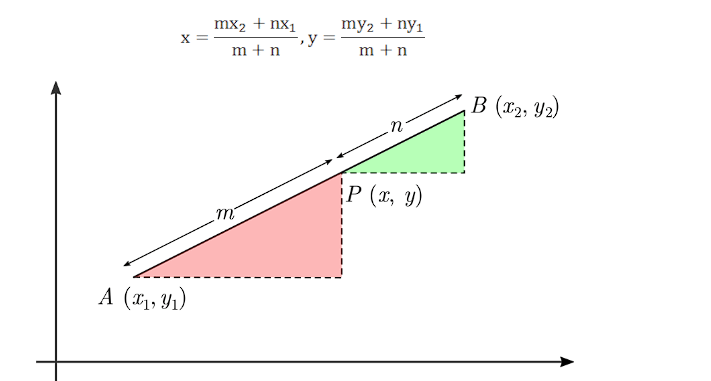
Note:
(i) If the point P divides the line segment joining A(x1, y1) and B(x2, y2) internally in the ratio k:1, its coordinates are given by:
Example 3: In what ratio does the point (2,- 5) divide the line segment joining the points A(-3, 5) and B(4, -9)?
Sol: Let the ratio be λ : 1
We have put m = λ and n = 1
or
But, coordinates of point is given as p(2,-5)
But, coordinates of point is given as p(2,-5)
4λ - 3 = 2(λ + 1)
⇒ 4λ = 2λ + 2 + 3⇒ 2λ = 5
⇒ λ = 5/2The required ratio is 5:2.
Mid -Point Formula
The mid-point of the line joining A(x1, y1) and B(x2, y2) is given as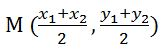
Example 4: Suppose we have two points A(2, 4) and B(6, 8). We want to find the midpoint of the line segment AB.
Sol:
Using the midpoint formula:Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
= ((2 + 6) / 2, (4 + 8) / 2)
= (8 / 2, 12 / 2)
= (4, 6)
Therefore, the midpoint of the line segment AB is M(4, 6).
Centroid of the Triangle (Deleted from NCERT)
The Centroid of the triangle is the point of intersection of medians of the triangle. For a triangle A(x1, y1), B(x2, y2) and C(x3, y3) we can say that the co-ordinates of centroid is given as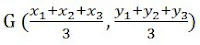
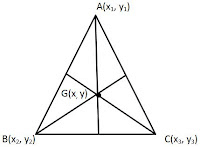
Example 4: A triangle has vertices at (-2, 4), (6, 2), and (4, -6). Find the coordinates of its centroid.
Sol:
To find the centroid of a triangle, we take the average of the x-coordinates and the average of the y-coordinates of the three vertices.
Average of x-coordinates = (-2 + 6 + 4) / 3 = 2
Average of y-coordinates = (4 + 2 - 6) / 3 = 0
Therefore, the coordinates of the centroid are (2, 0).
Areas of Triangle with Coordinates (Deleted from NCERT)
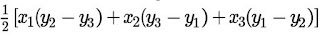
If you have the coordinates of the three vertices of the triangle (x1, y1), (x2, y2), and (x3, y3), you can use the Shoelace formula (also known as the Gauss area formula) to calculate the area:
Area = 0.5 x |(x1y2 + x2y3 + x3y1) - (y1x2 + y2x3 + y3x1)|
Example 5: For example, let's consider a triangle with vertices at (1, 2), (3, 5), and (6, 3)
Sol: Area = 0.5 x |(15 + 33 + 62) - (23 + 56 + 31)|
= 0.5 x |(5 + 9 + 12) - (6 + 30 + 3)|
= 0.5 x |26 - 39|
= 0.5 x |-13|
= 6.5 square units
Therefore, the area of the triangle is 6.5 square units.
Condition for Collinearity of three Points (Deleted from NCERT)
3 points A(x1, y1), It(x2, y2) and C (x3, y3) are said to be collinear if they are on same straight line. The condition for three points to be collinear is
{x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)} = 0
This is because the Area enclosed by these three points will be zero as they are on same line. Then by formula of area of triangle we can say that
1/2{x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)} = 0
⇒ {x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2) = 0
Example 6: Suppose we have three points: A(2, 4), B(4, 6), and C(6, 8). We will check if these points are collinear.
Sol: Using the condition for collinearity:
{x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)} = 0
Substituting the coordinates of the points:
{2(6 - 8) + 4(8 - 4) + 6(4 - 6)} = 0
Simplifying:
{-4 + 16 - 12} = 0
{-4} = 0
Since -4 is not equal to 0, the condition {x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)} = 0 is not satisfied.
Therefore, the points A(2, 4), B(4, 6), and C(6, 8) are not collinear.
Some Solved Questions
Q.1. Find the distance between the points (3, 5) and (-2, -1) using the distance formula.
Sol:
Using the distance formula:
d = √[(x2 - x1)² + (y2 - y1)²]
Substituting the coordinates:
d = √[(-2 - 3)² + (-1 - 5)²]
d = √[(-5)² + (-6)²]
d = √[25 + 36]
d = √61
Therefore, the distance between the points (3, 5) and (-2, -1) is √61 units.
Q.2. Find the coordinates of the midpoint of the line segment joining the points (-3, 2) and (5, -4).
Sol:
Using the midpoint formula:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Substituting the coordinates:
Midpoint = ((-3 + 5) / 2, (2 + (-4)) / 2)
Midpoint = (2 / 2, -2 / 2)
Midpoint = (1, -1)
Therefore, the midpoint of the line segment joining (-3, 2) and (5, -4) is (1, -1).
Q.3. Find the area of the triangle with vertices at (-2, 3), (4, -1), and (0, 6) using the Shoelace formula.
Sol:
Using the Shoelace formula:
Area = 0.5 x |(x1y2 + x2y3 + x3y1) - (y1x2 + y2x3 + y3x1)|
Substituting the coordinates:
Area = 0.5 x |(-2 x (-1) + 4 x 6 + 0 x 3) - (3 x 4 + (-1) x 0 + 6 x (-2))|
Area = 0.5 x |(2 + 24 + 0) - (12 + 0 - 12)|
Area = 0.5 x |26 - 0|
Area = 0.5 x 26
Area = 13 square units
Therefore, the area of the triangle with vertices (-2, 3), (4, -1), and (0, 6) is 13 square units.
Q.4.Determine whether the points (-2, -3), (1, -5), and (4, -7) are collinear.
Sol:
Using the condition for collinearity:
{x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)} = 0
Substituting the coordinates:
{-2(-5 - (-7)) + 1((-7) - (-3)) + 4((-3) - (-5))} = 0
Simplifying:
{-2(2) + 1(-4) + 4(2)} = 0
{-4 - 4 + 8} = 0
{0} = 0
Since 0 is equal to 0, the points (-2, -3), (1, -5), and (4, -7) are collinear.
|
127 videos|584 docs|79 tests
|
FAQs on Coordinate Geometry Class 10 Notes Maths Chapter 7
| 1. What is the Distance Formula in Coordinate Geometry? |  |
| 2. How is the Mid-Point Formula used in Coordinate Geometry? |  |
| 3. What is the Section Formula in Coordinate Geometry? |  |
| 4. How is the Centroid of a Triangle calculated using Coordinate Geometry? |  |
| 5. What is the Condition for Collinearity of Three Points in Coordinate Geometry? |  |