Cube Based Puzzles | IBPS PO Prelims & Mains Preparation - Bank Exams PDF Download
When we say Cube, we refer to the three dimensional solid with equal faces (total 6 faces).
Few things to remember while dealing with a cube:
- A cube has 6 faces
- A cube has 12 edges
- A cube has 8 vertices
Let us make a cut parallel to the base of the cube. We get two solids. If we make another cut parallel to the base, we get three solids. For n cuts mutually parallel to the base (or any other face), we get n+1 solid pieces.
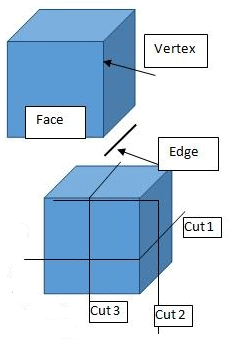
If we make one cut parallel to the base (say x-axis) and another cut perpendicular to the first cut (say y axis), the second cut will divide each of the two solids we get from the first cut into two pieces. We get total 4 pieces or 4 parts of the initial big cube. Similarly, another cut parallel to both the previous cuts (z-axis) will further divide these 4 pieces into two pieces each, thus making the total pieces as 8. When we analyze this, we see that when we make X mutually parallel cuts along x-axis, Y mutually parallel cuts along y axis and Z mutually paralel cuts along z axis we get (X+1)*(Y+1)*(Z+1) pieces of the original cube. X cuts along x itself will produce X+1 pieces and when we cut each of those pieces with Y cuts, each of them will produce Y+1 pieces and similar with Z cuts.
Total number of pieces obtained with X cuts in x axis, Y cuts in y axis and Z cuts in z axis =(X+1)*(Y+1)*(Z+1)
Note that, all the pieces will not necessarily be cubes. They can be cubes or cuboids. All the pieces are cubes when X = Y = Z and all the cuts are equidistant. This is the scenario when the number of cuts are given to us. Sometimes, we are given the sum of X + Y + Z instead of individual values.
MINIMUM NUMBER OF PIECES WITH A GIVEN TOTAL NUMBER OF CUTS
When we are given total number of cuts, the cuts can be made in any axis. Say if we make total 12 cuts, all 12 can be in x-axis, or 6 in x and 6 in y-axis etc. For a given number of cuts, we can have a number of combinations. We get the minimum number of pieces when all the cuts are made in the same axis. If we make all 12 cuts along x-axis, total 13 pieces are formed. All other combinations will result in more than 13 pieces. Let’s say, 11 cuts along x-axis and 1 cut along y. The total number of pieces formed is (11+1)*(1+1) = 24.
MAXIMUM NUMBER OF PIECES WITH A GIVEN TOTAL NUMBER OF CUTS
In order to get maximum number of pieces with given number of cuts, divide the total cuts equally among the three axis. If we divide 12 cuts equally among the three axis, we get 4 cuts in each axis resulting in (4+1)*(4+1)*(4+1) = 125 pieces overall. But what if the total number of cuts cannot be divided equally among the three axis. For a number like 14, we cannot distribute equally among all thethree axis. In such case, to maximize the total number of pieces, we need to minimize the difference between the number of cuts in any two axis is minimum. For 14 cuts, we can divide it as X = 5, Y = 5, Z = 4. Any other combination of numbers will result in a lower number of pieces. If we analyze, we see that in case of equal cuts, the difference between the numbers of cuts is zero that results in the maximum number of pieces.
NUMBER OF CUTS FROM TOTAL NUMBER OF PIECES GIVEN
The question can also mention the total number of pieces formed after a certain number of cuts. We need to find the number of cuts in different axis based upon the requirement of the question. Suppose, a cube is cut into 10 pieces. Now 10 = (X+1)*(Y+1)*(Z+1). Now 10 is to be represented as the product of 3 numbers or factors. We can have, 10 = 1*1*10 or 1*2*5.
Minimum numbers of cuts is obtained if we factorize the number of pieces into three equal factors. If three equal factors are not possible, then we should minimize the difference between the numbers.In case of 10 pieces, 1*2*5 gives minimum difference between factors.
To maximize the total number of cuts, all the cuts are made in one axis. For instance, for 10 pieces, factors are 10*1*1 that means the x-axis cuts are 9 and no cut is made in other two axis.
PAINTING THE OUTER SURFACE OF THE CUBE AFTER CUTTING
The most common type of cube question is painting the faces of the cube. Let us say, a cube is painted black, then it is cut into 64 pieces by 3 cuts in each directions. As we can see, there are 4 rows of 16 pieces (small cubes) each. Few conclusions from the figure 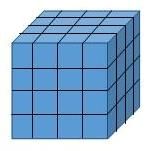
- Number of cubes with 3 faces painted black = all the corner cubes which is equal to 8 cubes.
- Number of cubes with exactly 2 faces painted = (n-2)*(number of edges) = (4-2)*(12) = 24.
- Number of cubes with exactly 1 face painted red = cubes on the faces (except on the edge and the corner) = (n – 2)2*6=24
- Number of cubes with 0 faces painted black = (n-2)3 = 8
The number of cubes that remain unaffected with the painting are those, which are not on the outer side. In other words, if we remove the outer painted shell then the inner structure is what we desire or we reduce the dimension of the cube by 2 units (remove a painted layer from all the sides or faces) to get a inner cube of side dimension = n-2 units.
If the number of cuts are not equal, let’s say if X = 5, Y = 6, Z = 7, then:
- Number of cubes with 3 faces painted black = all the corner cubes which is equal to 8 cubes.
- Number of cubes with exactly 2 faces painted = (X-2)*4 + (Y-2)*4 + (Z-2)*4 {since 4 edges will have each of (X-2),(Y-2),(Z-2)}= 12 + 16 + 20 = 48.
- Number of cubes with exactly 1 face painted red = cubes on the faces (except on the edge and the corner) = 2*[(X-2)(Y-2) + (Y-2)(Z-2) + (X-2)(Z-2)] = 2*(12 + 20 +15) = 94
- Number of cubes with 0 faces painted black = the inner cuboid = (X-2)*(Y-2)*(Z-2)= 3*4*5 = 60
IF FACES ARE PAINTED WITH A DIFFERENT COLOR
In the previous case, we saw the case when all the faces are painted with the same color. The question can also paint faces with a different color. Let us say the three pair of adjacent faces are painted with with Red, Blue and Green respectively. The cube is cut into 64 identical cubes with identical number of cuts along the three axis.
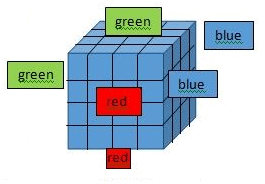
- We make the following observations:
Number of cubes with all the three color faces = 2 cubes diagonally opposite to each other. - Number of cubes with only same color faces on two faces = three edges without corner cubes = 3*(n-2) = 6
- Total cubes on the edges = 4*n + 8*(n-2) = 32
- Number of cubes with only 2 color faces = total cubes on edges – same color on two faces cubes – all three color face cubes = (3) – (2) = 32 – 6 – 2 = 24
- From the above observation, we can say cubes with only Red and Green faces or only blue and green = 24/3 = 8
- Number of cubes with exactly one face red = cubes on the two faces of the painted red surface = 2*(n-2)2 = 8
- Number of cubes with faces only red = (2)/3 + (6) = (n-2) + 2*(n-2)2 = 10
- Number of cubes with exactly one face painted = 6 faces with (n-2)2 cubes painted on one face = 6*(n-2)2 = 150.
- Number of cubes with exactly two surfaces painted with different colors = 9 edges with (n-2) cubes = 9*(n-2) = 18
It is a useful approach to make the cube diagram on the paper while solving the question. Cube is a 3-D figure and becomes challenging while solving without a figure, hence it is highly recommended that you make a cube figure while solving the cube questions.
Cubes can also be painted like opposite sides with similar colors or each layer with a different layer. The approach to every kind of question depends upon visualization of the figure. The 2-D diagram would assist a lot in solving but one needs to think more on the three faces hidden in the figure. Cube, being a symmetrical figure allows us to think in symmetrical terms in majority of the questions.
THE NUMBERED CUBES
Another type of cube question is the numbering of the smaller cubes after cutting the larger cube. Remember, the concept of cut could also be framed as ‘125 identical cubes are placed on one another in a manner such that they form a larger cube’,the approach for these questions would remain the same as discussed. Let us say there are 125 identical unit cubes numbered from 1 to 125 combined to form a larger cube to side 5 units. The cubes are always placed from left to right in ascending order of their numbers starting from the bottommost layer and the first row. After placing the first row, the next row is placed behind the first row such that the first cube of the next row comes directly behind the first cube of the first row. After completing the bottommost layer, the next layer is placed in a similar way the first layer was placed. Find the sum of the numbers of the cubes placed at the vertices.
From the above statement, we know that each row have 5 unit cubes. Let us make the bottom most layer of the larger cube.
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
Layer 1 (bottommost)
26 27 28 29 30
31 32 33 34 35
36 37 38 39 40
41 42 43 44 45
46 47 48 49 50
Layer 2
From the above placement of cubes we see that in bottom most layer cubes numbered 1, 5, 21, 25 are the vertex cubes. The topmost layer will have the other 4 cubes. To get the numbers of those cubes, we can either draw all the five layers or from the pattern we see that the last cube is a multiple of 25 in every layer. So the last cube in layer 4 will be 100. Let us draw the fifth layer.
101 102 103 104 105
106 107 108 109 110
111 112 113 114 115
116 117 118 119 120
121 122 123 124 125
Layer 5 (topmost)
The other 4 cubes are 101, 105, 121, 125. The sum of the 8 cubes is (1+5+21+25+101+105+121+125) = 504. If we want to save time, we analyze that the sum of the opposite vertex cubes is 126 or from the first layer itself, the sum of the diagonal cubes is 25*(layer number) + 1.
|
647 videos|1023 docs|305 tests
|
FAQs on Cube Based Puzzles - IBPS PO Prelims & Mains Preparation - Bank Exams
| 1. What are cube-based puzzles? |  |
| 2. How do cube-based puzzles work? |  |
| 3. What are some popular cube-based puzzles? |  |
| 4. How can I improve my skills in solving cube-based puzzles? |  |
| 5. Are cube-based puzzles beneficial for brain development? |  |

















