Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Cyclic Quadrilaterals
Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Cyclic Quadrilaterals
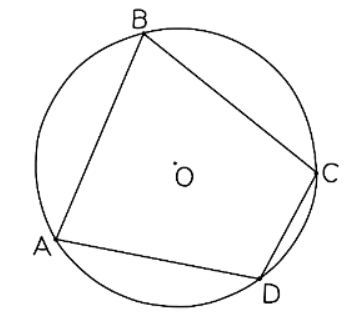
Circle Theorem: Opposite angles in a cyclic quadrilateral add up to 180°
- This theorem explains that in a cyclic quadrilateral, if all four vertices lie on the circumference of a circle, then the angles opposite to each other will sum up to 180°.
- A cyclic quadrilateral must have all its vertices on the circumference of a circle.
- The cyclic quadrilateral theorem is exclusive to cyclic quadrilaterals and does not apply to other types of quadrilaterals within a circle.
- For instance, a common scenario that does not involve a cyclic quadrilateral is depicted below:
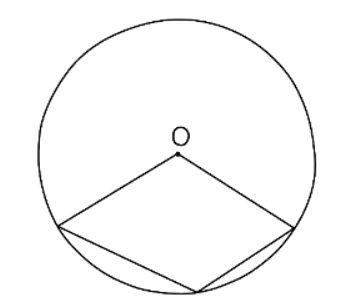
- When utilizing the cyclic quadrilateral theorem as a reason in an examination, it is essential to incorporate key vocabulary.
- In this context, opposite angles in a cyclic quadrilateral sum up to 180°.
- The term 'supplementary' denotes angles that add up to 180° and can also be utilized with specific reference to angles within a cyclic quadrilateral.
The document Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
109 videos|689 docs|60 tests
|
FAQs on Cyclic Quadrilaterals - Mathematics for GCSE/IGCSE - Class 10
| 1. How can I identify a cyclic quadrilateral? |  |
Ans. A cyclic quadrilateral is a quadrilateral where all four vertices lie on the circumference of a circle. To identify a cyclic quadrilateral, you can check if the sum of opposite angles is equal to 180 degrees.
| 2. What is the Cyclic Quadrilateral Theorem? | |
Ans. The Cyclic Quadrilateral Theorem states that the opposite angles of a cyclic quadrilateral are supplementary, meaning they add up to 180 degrees.
| 3. Can a quadrilateral be cyclic if all its sides are equal? | |
Ans. No, a quadrilateral with all sides equal is a rhombus, and not all rhombuses are cyclic quadrilaterals. A cyclic quadrilateral requires all four vertices to lie on the circumference of a circle.
| 4. How do I prove that a quadrilateral is cyclic? | |
Ans. To prove that a quadrilateral is cyclic, you can show that the sum of opposite angles is 180 degrees. Another method is to show that the quadrilateral can be inscribed in a circle.
| 5. Why is understanding cyclic quadrilaterals important in mathematics? | |
Ans. Understanding cyclic quadrilaterals is important in geometry as it helps in solving problems related to angles and circles. It also helps in proving theorems and properties of quadrilaterals.
About this Document
4.98/5
Rating
Sep 23, 2025
Last updated
Related Exams
Document Description: Cyclic Quadrilaterals for Class 10 2025 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Cyclic Quadrilaterals have been prepared according to the Class 10 exam syllabus. Information about Cyclic Quadrilaterals covers topics
like Cyclic Quadrilaterals and Cyclic Quadrilaterals Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Cyclic Quadrilaterals.
Introduction of Cyclic Quadrilaterals in English is available as part of our Mathematics for GCSE/IGCSE
for Class 10 & Cyclic Quadrilaterals in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10
Description
Full syllabus notes, lecture & questions for Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Cyclic Quadrilaterals
In this doc you can find the meaning of Cyclic Quadrilaterals defined & explained in the simplest way possible. Besides explaining types of
Cyclic Quadrilaterals theory, EduRev gives you an ample number of questions to practice Cyclic Quadrilaterals tests, examples and also practice Class 10
tests
Related Searches
Viva Questions
,MCQs
,Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10
,practice quizzes
,Extra Questions
,study material
,shortcuts and tricks
,Free
,Objective type Questions
,video lectures
,Important questions
,Semester Notes
,Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10
,mock tests for examination
,Cyclic Quadrilaterals | Mathematics for GCSE/IGCSE - Class 10
,Exam
,ppt
,Summary
,Previous Year Questions with Solutions
,Sample Paper
,past year papers
;
Additional Information about Cyclic Quadrilaterals for Class 10 Preparation
Cyclic Quadrilaterals Free PDF Download
The Cyclic Quadrilaterals is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Cyclic Quadrilaterals now and kickstart your journey towards success in the Class 10 exam.
Importance of Cyclic Quadrilaterals
The importance of Cyclic Quadrilaterals cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Cyclic Quadrilaterals Notes
Cyclic Quadrilaterals Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Cyclic Quadrilaterals.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Cyclic Quadrilaterals Notes on EduRev are your ultimate resource for success.
Cyclic Quadrilaterals Class 10 Questions
The "Cyclic Quadrilaterals Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Cyclic Quadrilaterals on the App
Students of Class 10 can study Cyclic Quadrilaterals alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Cyclic Quadrilaterals,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Cyclic Quadrilaterals is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup