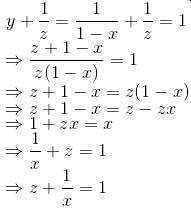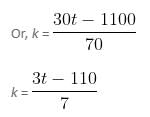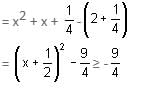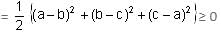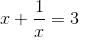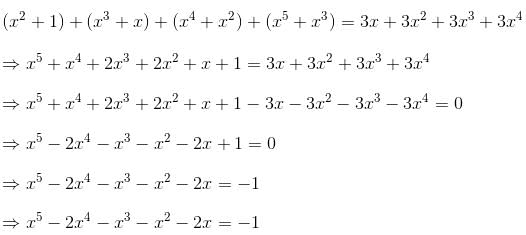CAT Exam > CAT Notes > 3 Months Preparation for CAT > Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Daily Practice Questions Questions for CAT with Answers PDF
This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Quadratic Equations & Linear Equations (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself: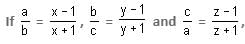
then which of the following is true?
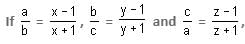
then which of the following is true?
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:The sum of ages of a group of teachers, doctors and lawyers is 2160 years and their average age is 36 years. If each teacher had been older by 1 year, each doctor by 6 years and each lawyer by 7 years, their average age would have increased by 5 years. Find the minimum possible number of doctors in the group.
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:What is the value of the expression 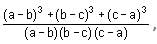 when a = 333, b = 444 and c = 555?
when a = 333, b = 444 and c = 555?
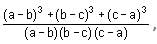 when a = 333, b = 444 and c = 555?
when a = 333, b = 444 and c = 555?
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:The number of real solutions of |x|2 + 3 |x| + 2 = 0 is
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:The condition that the roots of the equation lx2 + mx + n = 0 are in the ratio 3 : 4, is
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:How many possible integral values are there for m if it is known that m2 + 12m + 20 ≤ 0?
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:A and B had certain number of stamps. A said to B, ''If you give me one of your stamps, we shall have equal number of stamps''. B replies, ''If you give me one of your stamps, I shall have twice as many as you will be left with''. Find the total number of stamps with A and B.
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If p = x2 - yz, q = y2 - zx and r = z2 - xy, then the value of
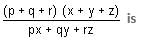
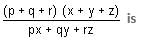
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If α, β and γ are the roots of the equation 2x3 - 3x2 - 5x + 6 = 0, then α2 + β2 + γ2 is equal to
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If a + b = 2c, then what is the value of
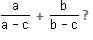
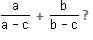
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:The set of value of λ for which both the roots of the equation x2 - (λ + 1)x + λ + 4 = 0 are negative, is
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If x2 = y + z, y2 = z + x and z2 = x + y, then the value of
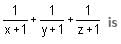
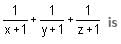
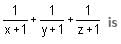
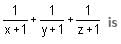
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If 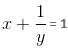 and
and 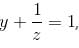 then
then 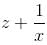 is equal to
is equal to
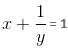 and
and 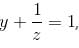 then
then 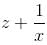 is equal to
is equal to
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:A famous cricketer Mr. Michael Swrfieai went to purchase a certain number of balls. There were two types of balls in the outlet: tennis balls and leather balls. A leather ball was 70 cents costlier than a tennis ball. If it is known that he purchased a total of 30 balls and spent $32(1$ = 100 cents) on purchasing the balls, what could be the possible cost of a tennis ball?
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If p, q are roots (non-zero) of the equation x2 + px + q = 0, then the least value of x2 + px + q is
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If x, y and z are real numbers, then x2 + 4y2 + 9z2 - 6yz - 3zx - 2xy is always
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If y = x - 1/x, the expression 5x4 + 3x3 - 7x2 - 3x + 5 can be expressed as
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:If 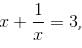 then find the value of (x5 - 2x4 - x3 - x2 - 2x)
then find the value of (x5 - 2x4 - x3 - x2 - 2x)
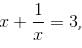 then find the value of (x5 - 2x4 - x3 - x2 - 2x)
then find the value of (x5 - 2x4 - x3 - x2 - 2x)
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:There is a father, a mother and 2 sons in a family and their total age is 60 years. The difference between the sons' age is 3 years, mother's age exceeds the sum of the sons' age by 17 years and the difference of age of father and mother is equal to the age of the elder son. How old is the father?
View Solution
Question for Practice Questions Level 2: Quadratic Equations & Linear Equations - 2
Try yourself:The values of a and b for which 3x3 - ax2 - 74x + b is a multiple of x2 + 2x - 24 are
View Solution
The document Daily Practice Questions Questions for CAT with Answers PDF is a part of the CAT Course 3 Months Preparation for CAT.
All you need of CAT at this link: CAT
|
321 videos|442 docs|280 tests
|
Related Searches

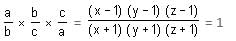
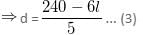
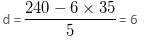
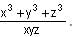
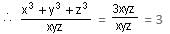
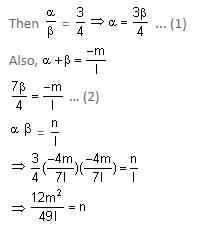
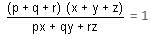
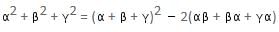
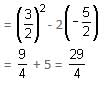
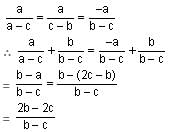
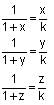
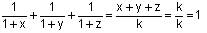
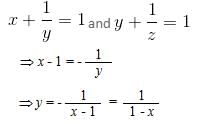
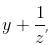 we get
we get