Decimals: Place Value & Power of 10 | Elementary Mathematics for CDS PDF Download
Place Value of decimals
The place value system is used to define the position of a digit in a number which helps to determine its value. When we write specific numbers, the position of each digit is important.
Example:
For instance, let’s consider the number 456.
- The position of “6” is in One’s place, which means 6 ones (i.e. 6).
- The position of “5” is in the Ten’s place, which means 5 tens (i.e. fifty).
- The position of “4” is in the Hundred’s place, which means 4 hundred.
- As we go left, each position becomes ten times greater.
Hence, we read it as “Four hundred fifty-six”.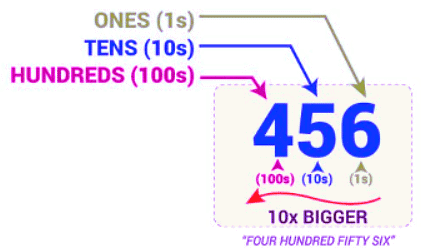
As we move left, each position is 10 times bigger!
Tens are 10 times bigger than Ones.
Hundreds are 10 times bigger than Tens.
And
Each time we move right every position becomes 10 times smaller from Hundred’s to Ten’s, to Ones
But if we continue past Ones?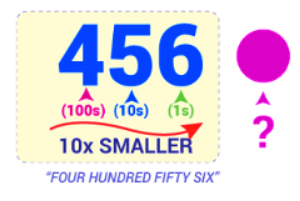
What are 10 times smaller than Ones?
Before that, we should first put a decimal point,
So we already know that where we put that decimal point.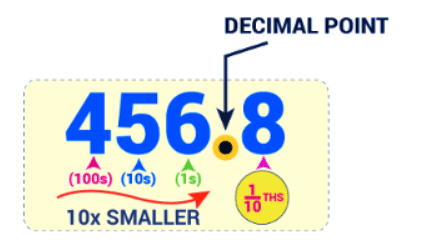 We say the above example as four hundred and fifty-six and eight-tenths but we usually just say four hundred and fifty-six point eight.
We say the above example as four hundred and fifty-six and eight-tenths but we usually just say four hundred and fifty-six point eight.
The power of 10 can be found using the following Place Value Chart: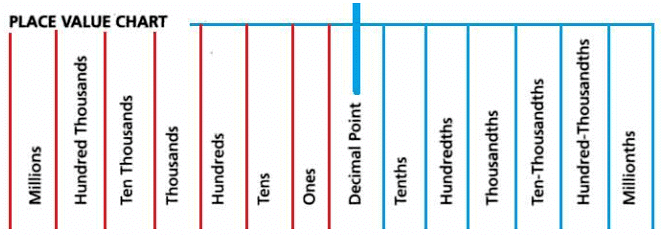
The digits to the left of the decimal point are multiplied with the positive powers of ten in increasing order from right to left.
The digits to the right of the decimal point are multiplied with the negative powers of 10 in increasing order from left to right.
Following the same example 81.75
The decimal expansion of this is:
{(8*10) + (1*1)} + {(7*0.1) + (5*0.01)}
Where each number is multiplied by its associated power of ten.
Power of 10
According to mathematics, the power of ten is any of the integers powers of the number multiplied by 10. In simple words, it means that we multiply ten by itself a certain number of times (when the power is a positive integer). Moreover, in the definition of the number 1 is a power (the zeroth power) of ten.
Scientific Notation Regarding Power of 10
Also, referred to as the ‘standard form,’ the scientific notation was given its name because firstly scientist employed it to represent very small and very big numbers. Furthermore, the power that 10 multiplied by is also called as exponents.
Besides, we can find them in positive form as well as a negative form. In addition, its positive form represents multiplication and negative form represents division.
In the notation index of 10 tells that from how many places the decimal points should move to the right. Conversely, for understanding this, consider we multiply 1.35 by 10 to the power fourth. Or 1.35 × 104.
Then you can calculate it as 1.35 × (10 × 10 × 10 × 10), or 1.35 × 10,000 which gives the answer 13,500. Now, if we were to move the decimal place in 1.35 over by four spots then you would also create 13,500.
The negative power of 10
We have many times faced situations where the power of ten is negative. Also, this indicates that the number should be divided by the negative power. For example, if we multiply 6 by 10 to the power negative three or 6 ÷ 10-3. Now you can write this as 6 ÷ (10 ÷ 10 ÷ 10) or 6 ÷ 1,000. Then we can simply move the decimal place over to the left three spaces. So, the answer to the question is 0.0006 and this is the numerical result for dividing 6 by 10 to the negative power 3.
Write Each Decimal as a Power of 10
It is possible to write each decimal as a power of 10. A practical example of 10s power is the way that we measure light-years or the distance travel by light n a span of one year, is spoken using scientific notation rather than writing down its entire numerical representation. Also, it’s easier for scientists to write its expression 9.461 × 1015meters relatively than 94,61,00,00,00,00,000 meters.
For evaluating the power of 10 we need to multiply the base 10 by itself the exponent amount of times.
Some examples are
- 10 × 10 = 100
- 10 × 10 × 10 = 1000
- 10 × 10 × 10 × 10 × 10 =1,00,000
And this process continues on to infinity.
The pattern of Power of 10
If you look closely then you will find that the number of zeros in the solution matches the exponent.
For example it the power of 10 is 2 then the answer is 100 which as two zeros. In the same way, if the power of 10 increases to 5 then the answer 1,00,000 has five zeros.
Solved Example
Example: What will be the notation form of 3,00,00,00,000 or 300 crores?
(a) 3 × 109
(b) 3 × 108
(c) 3 × 1010
(d) 3 × 1011
(e) None of these
Ans: (d)
Explantion: 3 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 3,00,00,00,000.
|
165 videos|95 docs|127 tests
|





















