Definite Integration and Its Properties | Mathematics (Maths) for JEE Main & Advanced PDF Download
Definite Integral Definition
The definite integral of a real-valued function f(x) with respect to a real variable x on an interval [a, b] is expressed as
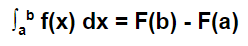
Here,
∫ = Integration symbol
a = Lower limit
b = Upper limit
f(x) = Integrand
dx = Integrating agent
Thus, ∫ab f(x) dx is read as the definite integral of f(x) with respect to dx from a to b.
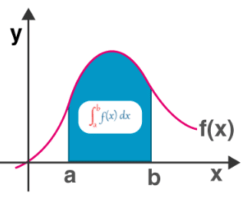
The Area Problem
Use rectangles to estimate the area under the parabola y = x2 from, 0 to 1 Wr first notice that the area of S must be somewhere between 0 and 1 because S is contained in a square with side length 1, but we can certainly do better than that. Suppose we divide S into four strips S1, S2, S3, and S4 by drawing the vertical lines x = 1/4, x = 1/2, x = 3/4,as in Figure (a)
We can approximate each strip by a rectangle whose base is the same as the strip and whose height is the same as the right edge of the strip [see Figure (b)]. In other words, the heights of this rectangle are the values of the function f(x) = x2 at the right endpoints of the subintervals
Each rectangle has a width of 1/4th and the heights are and 12. If we let R4 be the sum of the areas of these approximating rectangles, we get
From Figure (b) we see that the area A of S is less than R4, so A < 0.46875 Instead of using the rectangles in Figure (b) we could use the smaller rectangles in Figure (c) whose heights are the values of f at the left endpoints of the subintervals. (The leftmost rectangle has collapsed because its heights is 0). The sum of the areas of these approximating rectangles is
We see that the area of S is larger than L4, so we have lower and upper estimates for A , 0.21875 < A < 0.46875 We can repeat this procedure with a larger number of strips. Figure (d), (e) shows what happens when we divide the region S into eight strips of equal width. By computing the sum of the areas of the smaller rectangles (L8) and the sum of the areas of the larger rectangles (R8), we obtain better lower and upper estimates for A : 0.2734375 < A < 0.3984375
So one possible answer the question is to say that the true area of S lies somewhere between 0.2734375 and 0.3984375. We coluld obtain better estimates by increasing the number of strips.
Properties Of Definite Integral

1. Change of Variable: The definite integral is a number, it does not depend on x. In fact, we could use any letter in place of x without changing the value of the integral ;
=
2. Change of Limit: When we defined the definite integral f(x)dx, we implicity assumed that a < b. But the definition as a limit of sum makes sense even if a > b. Notice that if we reverse a and b, then Δx changes from (b – a)/n to (a – b)/n.
Therefore
3. Additivity With Respect To The Interval Of Integration :
This is not easy to prove in general, but for the casewhere f(x) ≥ 0 and a < c < b Property 7 can be seen from the geometric interpretation in Figure : The area under y = f(x) from a to c plus the area from c to b is equal to the total area from a to b.
Solved Examples
Ex.1 If it is known that
Sol. We have
= 17 -12 =5
Ex.2 Find
Sol. The function f defined by f(x) = 3 – 2x + x2 is continuous and has antiderivative g defined by Therefore, by the fundamental theorem of the calculus,
Ex.3 Evaluate
Sol. We can rewirte the integrand as follows
From this, you can rewrite the integral in two parts.
Ex.4 Evaluate dx, (where [ * ] denotes greatest integer function)
Sol.
Ex.5 Find the range of the function f(x) =
Sol. Given that
Proof :
In the first integral on the far right side we make the substitution u = –x. Then du = –dx and when x = –a, u = a.
Therefore
(a) If f is even, then
(b) If f is odd, then
Theorem is illustrated by Figure(a, b) For the case where f is positive and even, part(a) says that the area under y= f(x) from –a to a is twice the area from 0 to a because of symmetry. Thus, part (b) says the integral is 0 because the areas cancel.
Since f(x) = x6 + 1 satisfies f(–x) = f(x), it is even and so
Since f(x) = (tan x)/(1 + x2 + x4) satisfies f(–x) = –f(x), it is odd and so
Ex.6 Evaluate
Sol. The integrand, f(x) = x3 – 3x, is an an odd function; i.e., the equation f(–x) is satisifed for every x. Its graph, drwan in Figure, is therefore symmetric under reflection first about the x-axis and then about the y-axis. If follows that the region above the x-axis has the same areas as the region below it.
We conclude that = 0.
Ex.7 Evaluate where [x] denotes the greatest integer function less than or equal to x.
Sol.
Let Suppose f(x) = (–1)[x]
∴ f(–x) = (–1)[–x] = (–1)–1–[x], x ∉ l = - (-1)-[x]
= – f(x), f(x) is odd function.
Ex.8 Show that
Sol.
(By prop.) ........(1)
adding (1) and (2) we get 2l
(By prop.)
...(3)
...(4)
adding (3) and (4) we get
Ex.9 Evalute
Sol.
....(1)
Adding (1) and (2) we get 2l
Ex.10 Evaluate (where { * } denotes the fractional part function)
Sol.
= 1(0 + 1) + 15(1 – 0) = 16 (∴ {x} is a periodic function)
Ex.11 Let the function f be defined by f(x) =
Evaluate
Sol.
Ex.12 Evaluate where [x] and {x} denotes the integral part, and fractional part function of x and n ε N.
Sol.
Ex.13 Show that
Sol.
= q{(1 – 0) – (0 – 1)} + sin p – sin 0 = 2q + sin p
Ex.14 Evaluate (where [ * ] is the greatest integer function)
Sol.
Since sin x + cos x is periodic function with period 2π, so
Alternative Method : (Graphical Method)
It is clear from the figure.
|
177 videos|618 docs|160 tests
|
FAQs on Definite Integration and Its Properties - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of a definite integral? |  |
| 2. What are the properties of a definite integral? |  |
| 3. How can definite integration be used to solve real-world problems? |  |
| 4. What is the difference between a definite integral and an indefinite integral? |  |
| 5. Can the properties of definite integration be applied to improper integrals? |  |

















