Definition of Elastic Process
All bodies deform under the application of load. Depending on the characteristics of this deformation, the process or the body is classified as elastic or inelastic. The characteristics of this deformation depends on the material, temperature, magnitude of the applied load and among many other factors. Now, let us understand the characteristics of a elastic process.
Some of the definitions of an elastic process in the literature are:
1. The processes in which the original size and shape can be recovered is termed as elasticity.
2. Processes in which, the value of state variables in a given configuration are independent of how it was reached is called elastic.
3. A non-dissipative process is called a elastic process.
The first two definitions are popular in the literature. However, they are of little use because they cannot tell whether a process that the body is currently being subjected to is elastic. Such a conclusion can be arrived at only after subjecting the body to a complementary process. However, the last definition does not have such a drawback.
Further, it turns out that these various definitions are not equivalent. To see this, consider the uniaxial stress versus stretch ratio plot shown in figure 6.1a. Such a response, possible in shape memory alloys, would qualify as elastic only if the first definition is used. Since, the stress corresponding to a given stretch ratio depends on whether it is being loaded or unloaded it is not elastic according to the second definition. Also, since the loading and unloading path are different, there will be dissipation (wherein the mechanical energy is converted into thermal energy). Hence, it cannot be elastic by the last definition either.
Consider a axial stress vs. stretch response as shown in figure 6.1b which will be characterized as elastic according to definitions one and three. But the value of state variable stress could be anything corresponding to a stretch ratio of Λo. Hence, it is not elastic according to definition two. Of course, such a stress versus stretch response occurs for an idealized system made of a spring and an inextensible chord as shown in figure 6.1c. But then elasticity is an idealized process too and biological soft tissues response can be idealized as shown in figure 6.1b.
For us, a process is elastic only if it is consistent with all three definitions.
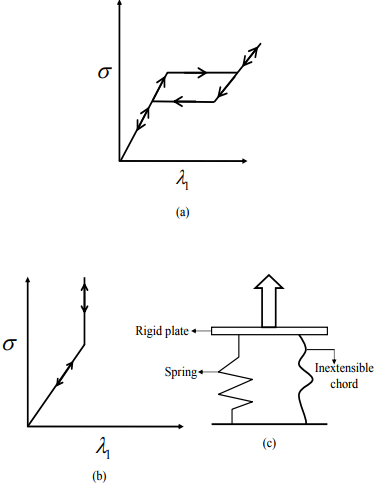
Figure 6.1: Uniaxial stress, σ versus axial stretch ratio, λ1 plot for (a) superelastic process (b) mechanical model shown in (c).
Before proceeding further a few words of caution is necessary. In reality, no process is elastic but some are close to being elastic. It is common in the literature, as we also did in the first paragraph, to call a material or a body to be elastic. This is incorrect, in a strict sense. It is the process that the body is being subjected to which is elastic. After all, the same body under different circumstances deforms inelastically.
Based on the above definition of elasticity, it can be shown that the Cauchy stress, σ, in an elastic process would at most depend on the deformation gradient, F, three material unit vectors, Mi and the state of Cauchy stress in the reference configuration4 , σR and thus,
g(σ, F,σR,M1,M2,M3) = 0. (6.1)
In other words, equation (6.1) is an assumption on how the state variable, stress, varies with the motion of the body. Since, by definition 2 for an elastic process, the value of stress cannot depend on the history of the motion field that the body has experienced, we are assured that there is an implicit function that relates the Cauchy stress and the deformation gradient.
We shall assume σR = 0, that is the reference configuration is stress free and that the Cauchy stress is related explicitly to the deformation gradient, so that equation (6.1) could be simplified to,
σ = h(F,M1,M2,M3). (6.2)
Further if we assume that the material is isotropic, that is the response of the material is same in all directions (see section 6.3.2 for more detailed discussion), the Cauchy stress would not depend on the three unit material vectors, Mi . For this case, the Cauchy stress depends explicitly only on the deformation gradient, i.e.,
σ = f(F). (6.3)
Thus, we have to find the relation between the six independent components of the stress tensor and the nine independent components of the deformation gradient. To find this relation in general through experimentation alone is daunting, as we illustrate now. Let us say the relation between the components of the Cauchy stress (σij ) and deformation gradient (Fkl) is linear and of the form,
σij = Cijkl(Fkl − δkl), (6.4)
| 4Do not confuse the stress in the reference configuration with Piola-Kirchhoff stresses. While σR = f(1,σR), Piola-Kirchhoff stress, P = det(F)f(F,σR)F−t . |
where Cijkl is the components of a constant fourth order tensor and δkl is the Kronecher delta. Even for this case, we have to find 6*9 = 54 constants which means we require 54 independent measurements. This is too many. While for metals this relationship is linear for polymers it is nonlinear. It is easy to see that the number of constants required in case of nonlinear relationship would be much higher than the linear case. Hence, if there is some way by which we can reduce the number of unknown functions from 6 and the variables that it depends on from 9 in equation (6.3) it would be useful.
























