Engineering Mathematics Exam > Engineering Mathematics Notes > Engineering Mathematics > Degree Sequence of a Graph
Degree Sequence of a Graph | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
- Given an undirected graph, a degree sequence is a monotonic nonincreasing sequence of the vertex degrees (valencies) of its graph vertices. The number of degree sequences for a graph of a given order is closely related to graphical partitions. The sum of the elements of a degree sequence of a graph is always even due to fact that each edge connects two vertices and is thus counted twice (Skiena 1990, p. 157).
- The minimum vertex degree in a graph G is denoted delta(G), and the maximum vertex degree is denoted Delta(G) (Skiena 1990, p. 157). A graph whose degree sequence contains only multiple copies of a single integer is called a regular graph. A graph corresponding to a given degree sequence d can be constructed in the Wolfram Language using RandomGraph [DegreeGraphDistribution[d]].
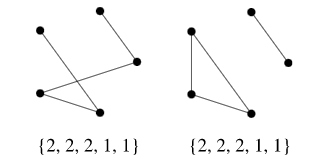
- It is possible for two topologically distinct graphs to have the same degree sequence. Moreover, two distinct convex polyhedra can even have the same degree sequence for their skeletons, as exemplified by the triangular cupola and tridiminished icosahedron Johnson solids, both of which have 8 faces, 9 vertices, 15 edges, and degree sequence (3, 3, 3, 3, 3, 3, 4, 4, 4).
- The number of distinct degree sequences for graphs of n=1, 2, ... nodes are given by 1, 2, 4, 11, 31, 102, 342, 1213, 4361, ... (OEIS A004251), compared with the total number of nonisomorphic simple undirected graphs with n graph vertices of 1, 2, 4, 11, 34, 156, 1044, ... (OEIS A000088). The first order having fewer degree sequences than number of nonisomorphic graphs is therefore n=5. For the graphs illustrated above, the degree sequences are given in the following table.

- The possible sums of elements for a degree sequence of order n are 0, 2, 4, 6, ..., n(n-1).
- A degree sequence is said to be k-connected if there exists some k-connected graph corresponding to the degree sequence. For example, while the degree sequence {1,2,1} is 1- but not 2-connected, {2,2,2} is 2-connected.
The document Degree Sequence of a Graph | Engineering Mathematics - Engineering Mathematics is a part of the Engineering Mathematics Course Engineering Mathematics.
All you need of Engineering Mathematics at this link: Engineering Mathematics
|
65 videos|129 docs|94 tests
|
Related Searches
















