Class 11 Exam > Class 11 Notes > Deriving the centripetal acceleration formula - Class 11
Deriving the centripetal acceleration formula - Class 11 PDF Download
What is centripetal acceleration and derive its formula also?
Ref: https://edurev.in/question/702216/What-is-centripetal-acceleration-and-derive-its-formula-also-
A body that moves in a circular motion (of radius r) at constant speed (v) is always being accelerated. The acceleration is at right angles to the direction of motion (towards the center of the circle) and of magnitude v2 / r.
The direction of acceleration is deduced by symmetry arguments. If the acceleration pointed out of the plane of the circle, then the body would leave the plane of the circle; it doesn't, so it isn't. If the acceleration pointed in any direction other than perpendicular (left or right) then the body would speed up or slow down. It doesn't.
Now for the magnitude. Consider the distance traveled by the body over a small time increment Δt:
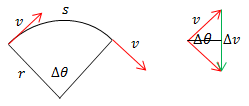
We can calculate the arc length s as both the distance traveled (distance = rate * time = v Δt) and using the definition of a radian (arc = radius * angle in radians = r Δθ:)
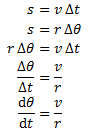
The angular velocity of the object is thus v / r (in radians per unit of time.)
The right half of the diagram is formed by putting the tails of the two v vectors together. Note that Δθ is the same in both diagrams.
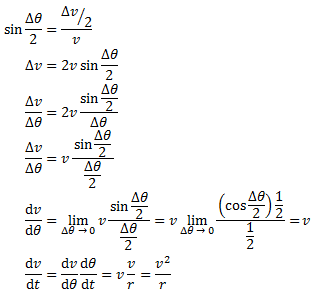
FAQs on Deriving the centripetal acceleration formula - Class 11
| 1. How can I derive the centripetal acceleration formula? |  |
Ans. To derive the centripetal acceleration formula, we can start with the basic equation for centripetal acceleration, which is given by a = v^2/r. This equation relates the centripetal acceleration (a) to the velocity (v) and the radius (r) of the circular path. By manipulating this equation and using the definitions of velocity and acceleration, we can derive the centripetal acceleration formula.
| 2. What is the significance of centripetal acceleration? | |
Ans. Centripetal acceleration is important because it describes the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its circular path. Without centripetal acceleration, an object would move in a straight line tangent to the circle instead of following a curved path.
| 3. How does centripetal acceleration differ from tangential acceleration? | |
Ans. Centripetal acceleration and tangential acceleration are both components of the total acceleration of an object moving in a circular path. Centripetal acceleration is directed towards the center of the circle and is responsible for changing the direction of motion. Tangential acceleration, on the other hand, is directed tangent to the circle and is responsible for changing the speed of the object. While centripetal acceleration always exists in circular motion, tangential acceleration may or may not be present, depending on whether the object's speed is changing.
| 4. Can centripetal acceleration ever be zero? | |
Ans. No, centripetal acceleration cannot be zero as long as an object is moving in a circular path. Centripetal acceleration is a result of the object's velocity changing direction, and even if the object is moving at a constant speed, it will still experience centripetal acceleration. The only way for centripetal acceleration to be zero is if the object is not moving in a circular path but is instead moving in a straight line.
| 5. How does centripetal acceleration relate to centripetal force? | |
Ans. Centripetal acceleration and centripetal force are closely related. According to Newton's second law of motion, the net force acting on an object is equal to the mass of the object multiplied by its acceleration. In the case of circular motion, the net force acting on the object is the centripetal force, which is directed towards the center of the circle. Therefore, the centripetal force can be calculated using the formula F = ma, where a is the centripetal acceleration. In this way, centripetal acceleration provides a link between the motion of an object and the force required to keep it moving in a circular path.
Related Exams
About this Document
|
1.8K Views |
|
4.73/5 Rating |
|
Nov 24, 2024 Last updated |
Document Description: Deriving the centripetal acceleration formula - Class 11 for Class 11 2024 is part of Class 11 preparation. The notes and questions for Deriving the centripetal acceleration formula - Class 11 have been prepared according to the Class 11 exam syllabus. Information about Deriving the centripetal acceleration formula - Class 11 covers topics like and Deriving the centripetal acceleration formula - Class 11 Example, for Class 11 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Deriving the centripetal acceleration formula - Class 11.
Introduction of Deriving the centripetal acceleration formula - Class 11 in English is available as part of
our Class 11 preparation & Deriving the centripetal acceleration formula - Class 11 in Hindi for Class 11
courses. Download more important topics, notes, lectures and mock test series for Class 11
Exam by signing up for free. Class 11: Deriving the centripetal acceleration formula - Class 11
Description
Full syllabus notes, lecture & questions for Deriving the centripetal acceleration formula - Class 11 - Class 11 | Plus excerises question with solution to help you revise complete syllabus | Best notes, free PDF download
Information about Deriving the centripetal acceleration formula - Class 11
In this doc you can find the meaning of Deriving the centripetal acceleration formula - Class 11 defined & explained in the simplest way possible.
Besides explaining types of Deriving the centripetal acceleration formula - Class 11 theory,
EduRev gives you an ample number of questions to practice Deriving the centripetal acceleration formula - Class 11 tests, examples and also practice Class 11 tests.
Download as PDF
|
Explore Courses for Class 11 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
MCQs
,Previous Year Questions with Solutions
,Viva Questions
,Deriving the centripetal acceleration formula - Class 11
,study material
,ppt
,Deriving the centripetal acceleration formula - Class 11
,Extra Questions
,Exam
,Objective type Questions
,Deriving the centripetal acceleration formula - Class 11
,practice quizzes
,Sample Paper
,video lectures
,Semester Notes
,past year papers
,shortcuts and tricks
,Free
,mock tests for examination
,Summary
,Important questions
;
Additional Information about Deriving the centripetal acceleration formula - Class 11 for Class 11 Preparation
Deriving the centripetal acceleration formula - Class 11 Free PDF Download
The Deriving the centripetal acceleration formula - Class 11 is an invaluable resource that delves deep into the core of the Class 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Deriving the centripetal acceleration formula - Class 11 now and kickstart your journey towards success in the Class 11 exam.
Importance of Deriving the centripetal acceleration formula - Class 11
The importance of Deriving the centripetal acceleration formula - Class 11 cannot be overstated, especially for Class 11 aspirants.
This document holds the key to success in the Class 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Deriving the centripetal acceleration formula - Class 11 Notes
Deriving the centripetal acceleration formula - Class 11 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Deriving the centripetal acceleration formula - Class 11.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Deriving the centripetal acceleration formula - Class 11 Notes on EduRev are your ultimate resource for success.
Deriving the centripetal acceleration formula - Class 11 Class 11 Questions
The "Deriving the centripetal acceleration formula - Class 11 Class 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Deriving the centripetal acceleration formula - Class 11 on the App
Students of Class 11 can study Deriving the centripetal acceleration formula - Class 11 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Deriving the centripetal acceleration formula - Class 11,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Deriving the centripetal acceleration formula - Class 11 is prepared as per the latest Class 11 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup